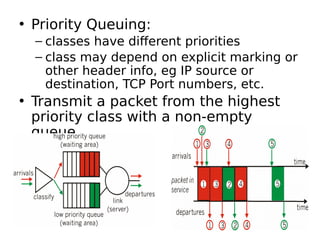
This document outlines two assignments for a course on data structures and files. The first assignment involves implementing a stack using a linked list and using it for infix, postfix, and prefix notation conversions and evaluations. The second assignment involves implementing a priority queue using a linked list to service patients in a hospital based on priority of illness. Key algorithms for stack, queue, and priority queue operations are described.

1. A Presentation
on
Data Structure and Files
Laboratory (214455)
Prepared By
Ms. K.D. Patil
Assistant Professor, Dept. of IT
Sanjivani College of Engineering, Kopargaon.

2. Teaching & Examination Scheme
• Teaching Scheme:
– Practical : 4 Hours/Week
• Credits:
– 02
• Examination Scheme:
– Term Work : 25 Marks
– External Practical : 50 Marks

3. Course Objectives
• To study data structures and their
implementations using OOP (C++)
and their applications
• To study some advanced data
structures such as trees, graphs and
tables
• To learn different file organizations

4. Course Outcomes
• After successful completion of this course,
student will be able to
– Apply and implement algorithm to illustrate use of
linear data structures such as stack, queue
– Apply and implement algorithms to
create/represent and traverse non-linear data
structures such as trees, graphs etc
– Apply and implement algorithms to create and
manipulate database using different file
organizations
– Learn and apply the concept of hashing in database
creation and manipulation

5. Assignment No. 1
• Aim:
– To implement stack as an abstract data
type using linked list and use this ADT
for conversion of infix expression to
postfix, prefix and evaluation of postfix
and prefix expression.

6. What is stack??
• It is a linear data structure in which
the insertion and deletion operations
are performed at only one end called
as ‘top’
• Inserting an item is known as
“pushing” onto the stack. “Popping”
off the stack is removing an item
• It is called as Last in First Out Data
structure.

7. Disadvantages of Stack using
Array
• The size of the stack must be
determined when a stack object is
declared
• Space is wasted if we use less
elements
• We cannot "push" more elements
than the array can hold

8. Stack as ADT
• Allocate memory for each new
element dynamically using linked list
• Each node in the stack should
contain two parts:
– data: the user's data
– next: the address of the
next element in the stack

9. Stack as ADT
• A stack is an abstract data type (ADT) that
supports two main methods:
– push(x): Inserts object x onto top of stack
– pop(): Removes the top object of stack and returns it;
if stack is empty an error occurs
• The following support methods should also be
defined:
– size(): Returns the number of objects in stack
– isEmpty(): Return a boolean indicating if stack is
empty.
– top(): return the top object of the stack, without
removing it; if the stack is empty an error occurs.

10. Node & Class Structure
Node Structure
• struct node
{
int data;
node* next;
};
Class Structure
•class Stack
{
private:
struct node * top; // Will always point to the head of
the list (First element)
public:
Stack()
{
top=NULL;
} // Default Constructor
void push(int);
int pop();
int getTop(); // returns the top-most element.
int isEmpty(); // returns true if the Stack is Empty,
else return false.
};

11. Algorithm
push
{
struct node *p;
p = new node;
p->data=value;
p->next = top;
top = p;
}
isEmpty()
{
If (top == NULL)
Return true;
Else
Return False;
}
pop
if(top != NULL)
{
Struct node *p;
p = top->data;
p = top;
top = top->next;
delete p;
}
getTop()
{
if(top)
return top->data;
else
return -1;
}

12. Expressions (Polish Notations)
• An expression is a collection of
operators and operands that
represents a specific value.
• Based on the operator position,
expressions are divided into THREE
types. They are as follows...
• Infix Expression eg. a+b
• Postfix Expression eg. ab+
• Prefix Expression eg. +ab

13. Algorithm: Infix to Postfix
Conversion
• Algorithm(infixtopostfix)
• Create stack
• Set postfix to null string
• i=0
• for all tokens ‘ch’ in the infix expression
• token=ch[i]
• if(token=‘(’)
– Push(stack, token)
• elseif(token=‘)’)
– Pop(stack, token)
– while(token!=‘(’)
- append token to postfix expression
- pop(stack, token)

14. • elseif(token==‘operator’)
–// test the priority of token to token at top of stack
–Stacktop(stack, toptoken)
–While(!stack.isEmpty() && priority(token)<=priority(toptoken))
-Pop(stack, tokenout)
-Append tokenout to postfix expression
-Stacktop(stack, toptoken)
–End while
–Push(stack,token)
• else
–// token is operand
–Append it to the postfix expression
• endif
• i=i+1
• end loop
• while(!stack.isempty())
–popstack(stack,token)
–Append token to postfix expression
• end while
• return postfix
• end infixtopostfix

15. Algorithm: Postfix Evaluation
• exprsize=length of string
• Initialize(stack s)
• x=readtoken()
• while(x)
• If(x is operand)
Push x onto stack
• If(x is operator)
{
Opnd2=pop(stack)
Opnd1=pop(stack)
Evaluate(opnd1,opnd2,operator x);
}
x=readnexttoken;
}

16. Algorithm: Prefix Evaluation
• exprsize=length of string
• Initialize(stack s)
• x=readtoken() // read token from right to left
• while(x)
• If(x is operand)
Push x onto stack
• If(x is operator)
{
Opnd2=pop(stack)
Opnd1=pop(stack)
Evaluate(opnd2,opnd1,operator x);
}
x=readnexttoken;
}

17. Application
• Stacks in the Java Virtual Machine
– Each process running in a Java program has its own Java
Method Stack.
– Each time a method is called, it is pushed onto the stack.
– The choice of a stack for this operation allows Java to do
several useful things:
- Perform recursive method calls
- Print stack traces to locate an error
• Java also includes an operand stack which is used to
evaluate arithmetic instructions, i.e.
Integer add(a, b):
OperandStack Op
Op.push(a)
Op.push(b)
temp1 ¬ Op.pop()
temp2 ¬ Op.pop()
Op.push(temp1 + temp2)

18. Outcome
• After successful completion of this
assignment, student will be able to
apply and implement algorithm to
illustrate use of stack linear data
structures.

19. Assignment 2
• Aim:
– Implement priority queue as ADT using
single linked list for servicing patients in
an hospital with priorities as i) Serious
(top priority) ii) medium illness (medium
priority) iii) General (Least priority).

20. What is Queue?
• Linear data structure which follows
FIFO (First In First ) principle.
• Allocate memory for each new
element dynamically
• Link the queue elements together
• Use two pointers, qFront and qRear
to mark the front and rear of the
queue

21. Queue as ADT
• A queue is an abstract data type
(ADT) that supports two main
methods:
– Enqueue(x): Inserts object x from rear
end
– Dequeue(): Removes the object x from
front end

22. Node & Class structure
Node Structure
• struct node
{
int data;
node* next;
};
Class Structure
• class queue
{
private:
struct node * front,
*rear;
public:
queue()
{
front=rear=NULL;
} // Default
Constructor
void enqueue();
void dequeue();

23. Algorithm
Enqueue()
{
struct node *ptr;
ptr=new node;
ptr->data=value;
ptr->next=NULL;
if(front == NULL)
{
front = rear = ptr;
rear->next = NULL;
}
else
{
rear->next = ptr;
rear = ptr;
rear->next = NULL;
}
}
Dequeue
{
struct node *ptr;
if(front==NULL)
{
cout<<"Queue is empty";
}
else
{
ptr=front;
x=ptr->data
front=front->next;
delete ptr;
}
}

24. Priority Queue
• Priority queues are a generalization of queues.
• Rather than inserting and deleting elements in
a fixed order, each element is assigned a
priority represented by an integer.
• We always remove an element with the
highest priority, which is given by the minimal
integer priority assigned.
• If two elements have the same priority, they
are served according to their order in the
queue.

25. Priority queue as ADT
Node Structure
• struct node
{
int priority;
int info; struct
node *link;
};
Class Structure
class Priority_Queue
{
private:
node *front;
public:
Priority_Queue()
{
front = NULL;
}
}

26. Algorithm
Enqueue
• void insert(int item, int priority)
{
node *tmp, *q;
tmp = new node;
tmp->info = item;
tmp->priority = priority;
if (front == NULL || priority < front->priority)
{
tmp->link = front;
front = tmp;
}
else
{
q = front;
while (q->link != NULL && q->link->priority <=
priority)
q=q->link;
tmp->link = q->link;
q->link = tmp;
}
}
Dequeue
• void del()
{
node *tmp;
if(front == NULL)
cout<<"Queue Underflown";
else
{
tmp = front;
cout<<"Deleted item is: "<<tmp-
>info<<endl;
front = front->link;
free(tmp);
}
}

27. Applications
• In an operating system the runnable
processes might be stored in a priority
queue, where certain system processes are
given a higher priority than user processes.
• CPU Scheduling
http://cs.uttyler.edu/Faculty/Rainwater/COSC
3355/Animations/priority.htm
• In a network router packets may be routed
according to some assigned priorities.

28. • Priority Queuing:
– classes have different priorities
– class may depend on explicit marking or
other header info, eg IP source or
destination, TCP Port numbers, etc.
• Transmit a packet from the highest
priority class with a non-empty
queue

29. Outcome
• After successful completion of this
assignment, student will be able to
apply and implement algorithm to
illustrate use of queue linear data
structures.