The document discusses queues and their implementation and applications. It begins by describing the physical nature of queues and some real-world examples where queues are used, such as waiting in line. It then defines queues as abstract data types and common queue operations like enqueue and dequeue. The document provides examples of implementing queues using arrays and linked lists, including pseudocode for basic queue methods. It also demonstrates using queues in C# code and discusses edge cases like empty queues.

1. Data Structures, Algorithms
Queue C#
Prof Hesham Arafat Ali

2. 2
Queues Everywhere!

3. Physical Nature of the QueuePhysical Nature of the Queue

4. Physical Nature of the QueuePhysical Nature of the Queue

5. 5
Queue ApplicationsQueue Applications
Real-World ApplicationsReal-World Applications
Buy a movie ticket
Check out at a bookstore
Bank / ATM
Call an airline
Cashier lines in any store
Computer Science ApplicationsComputer Science Applications
OS task scheduling
Print lines of a document
Printer shared between computers
Convert digit strings to decimal
Shared resource usage (CPU, memory access, …)

6. QueuesQueues
A queue represents a waiting list
A queue can be viewed as a special type of
list, where the elements are inserted into the end
(tail) of the queue, and are accessed and deleted
from the beginning (head) of the queue
6
Data1
Data2
Data1 Data1
Data2
Data3
Data1 Data2 Data3
Data2
Data3
Data1
Data3
Data2 Data3

7. Queue Abstract Data Type
ADT queue FIFO(First In First Out)
ordered list
all insertions are made at one end called
“rearrear”
all deletions are made at the other end
called “frontfront”
inserting and deleting elements in queue
rearA
rearB
A
rearC
B
A
rearD
C
B
A
rearD
C
B frontfrontfrontfront
front

8. Queue DefinitionQueue Definition
Is a container which provides exactly one method,
enqueueenqueue, for putting objects at the rear of the
container, and one method, dequeuedequeue, for taking
objects out of the container at the front.
container of objects that are inserted and removed
according to the first-in first-out (FIFOFIFO) principle.
Queue A data structure in which elements are added
to the rear and removed from the front; a "first in, first
out" (FIFO)

9. MethodsMethods
enqueue(o)enqueue(o) insert object o at the rear of
the queue
Input: Object; Output: None
dequeue()dequeue() removes and return the object at the
front of the queue; an error occurs if the
Input: None; Output: Object

10. MethodsMethods
size( )size( ) return the number of objects in the queue
Input: None; Output: Integer
isEmpty( )isEmpty( ) return a Boolean indicating if
the queue is empty
Input: None; Output: Boolean
front( )front( ) returns the front object in the queue, without
removing it; an error occurs if the queue is empty
Input: None; Output: Object

11. Array ImplementationArray Implementation
The easiest implementation also keeps
track of the number of items in the
queue and the index of the first
element (at the front of the queue), the
last element (at the rear).
[ 0 ][ 0 ] [1][1] [ 2 ][ 2 ] [ 3 ][ 3 ] [ 4 ][ 4 ] [ 5 ][ 5 ] . . .. . .
4 8 6
sizesize3
firstfirst0
lastlast2

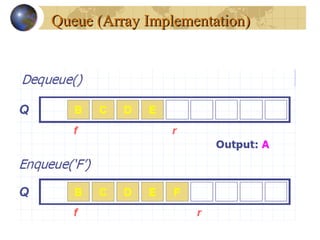
12. A Dequeue OperationA Dequeue Operation
When an element leaves the queue,
size is decremented, and first
changes, too.
[ 0 ][ 0 ] [1][1] [ 2 ][ 2 ] [ 3 ][ 3 ] [ 4 ][ 4 ] [ 5 ][ 5 ] . . .. . .
4 8 6
sizesize2
firstfirst1
lastlast2

13. An Enqueue OperationAn Enqueue Operation
When an element enters the
queue, size is incremented, and
last changes, too.
[ 0 ][ 0 ] [1][1] [ 2 ][ 2 ] [ 3 ][ 3 ] [ 4 ][ 4 ] [ 5 ][ 5 ] . . .. . .
28 6
sizesize3
firstfirst1
lastlast3

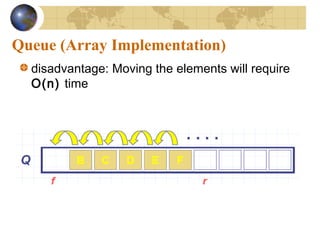
14. At the End of the ArrayAt the End of the Array
There is special behavior at the end of
the array. For example, suppose we
want to add a new element to this
queue, where the last index is [5]:
[ 0 ][ 0 ] [1][1] [ 2 ][ 2 ] [ 3 ][ 3 ] [ 4 ][ 4 ] [ 5 ][ 5 ]
2 16
sizesize3
firstfirst3
lastlast5

15. At the End of the ArrayAt the End of the Array
The new element goes at the front of
the array (if that spot isn’t already
used):
[ 0 ][ 0 ] [1][1] [ 2 ][ 2 ] [ 3 ][ 3 ] [ 4 ][ 4 ] [ 5 ][ 5 ]
2 16
sizesize4
firstfirst3
lastlast0
4

16. Queue Illustration
enqueue(D)
enqueue(A)
dequeue( )

17. enqueue(T)
enqueue(U)
enqueue(M)
front( )

18. isEmpty( )
size( )

19. Queue (Array Implementation)

20. Queue (Array Implementation)Queue (Array Implementation)

21. Queue (Array Implementation)

22. Sample Queue Operation

23. Queue (Array Implementation)
disadvantage: Moving the elements will require
O(n) time

24. Queue (Array Implementation)

25. Queue (Array Implementation)

26. Linked List ImplementationLinked List Implementation
10
15
7
null
13
A queue can also be
implemented with a linked list
with both a head and a tail
pointer.
head_ptr
tail_ptr

27. Queue (Array Implementation)
f is an index to cell of Q that stores the first
element of the queue (unless the queue is empty:
f = r)
r is an index to the next available array cell in
Q
initially, f = r = 0.

28. To get the value of r, we compute:
(r+1) mod N
To get the value of f, we compute:
(f+1) mod N
To get the size of the Queue:
(N-f+r) mod N

29. 29
ADT Queue
Specification:
Operations
• Create an empty queue
• Create a copy of a queue
• Destroy a queue
• Check if a queue is empty / Full
• Enqueue (Enq, Enque, Add, Insert) new element to the back (rear)
• Dequeue (Deq, Deque, Remove, Serve, Delete) an element from
the front
• Retrieve an element from a queue
Like the stack, if we need to modify an item in the queue,
we must remove it, change its contents, and then add it
back to the queue

30. Enqueue and dequeue
using System;
using System.Collections;
class MainClass {
public static void Main() {
Queue q = new Queue();
q.Enqueue(1);
q.Enqueue(2);
q.Enqueue(3);
q.Enqueue(4);
Console.Write("queue: ");
foreach(int i in q)
Console.Write(i + " ");
Console.WriteLine();
Console.Write("Dequeue -> ");
int a = (int) q.Dequeue();
Console.WriteLine(a);
Console.Write("queue: ");
foreach(int i in q)
Console.Write(i + " ");
Console.WriteLine();
}
}
queue: 1 2 3 4
Dequeue -> 1
queue: 2 3 4

31. Put elements into a queue
using System;
using System.Collections;
using System.Collections.Generic;
using System.Text;
class Program {
static void Main(string[] args) {
Queue alphabet = new Queue();
alphabet.Enqueue("A");
alphabet.Enqueue("B");
alphabet.Enqueue("C");
Console.Write("First Iteration: ");
foreach (string item in alphabet) {
Console.Write(item);
}
Console.WriteLine("nItem pulled from collection: " +
alphabet.Dequeue().ToString());
Console.Write("Second iteration: ");
foreach (string item in alphabet) {
Console.Write(item);
} } }
First Iteration: A B C
Item pulled from collection: A
Second Iteration: B C

32. Clear a Queue
using System;
using System.Collections;
class MainClass
{
static void Main(string[] args)
{
Queue a = new Queue(10);
int x = 0;
a.Enqueue(x);
x++;
a.Enqueue(x);
foreach (int y in a)
{
Console.WriteLine(y);
}
a.Dequeue();
a.Clear();
}
}
0
1

33. Demonstrate the Queue classDemonstrate the Queue class
// Demonstrate the Queue class.
using System;
using System.Collections;
public class QueueDemo {
static void showEnq(Queue q, int a) {
q.Enqueue(a);
Console.WriteLine("Enqueue(" + a + ")");
Console.Write("queue: ");
foreach(int i in q)
Console.Write(i + " ");
Console.WriteLine();
}
static void showDeq(Queue q) {
Console.Write("Dequeue -> ");
int a = (int) q.Dequeue();
Console.WriteLine(a);
Console.Write("queue: ");
foreach(int i in q)
Console.Write(i + " ");
// Demonstrate the Queue class.
using System;
using System.Collections;
public class QueueDemo {
static void showEnq(Queue q, int a) {
q.Enqueue(a);
Console.WriteLine("Enqueue(" + a + ")");
Console.Write("queue: ");
foreach(int i in q)
Console.Write(i + " ");
Console.WriteLine();
}
static void showDeq(Queue q) {
Console.Write("Dequeue -> ");
int a = (int) q.Dequeue();
Console.WriteLine(a);
Console.Write("queue: ");
foreach(int i in q)
Console.Write(i + " ");

34. sing System;
using System.Collections;
public class QueueDemo {
static void showEnq(Queue q,
int a) {
q.Enqueue(a);
Console.WriteLine("Enqueue(
" + a + ")");
Console.Write("queue: ");
foreach(int i in q)
Console.Write(i + " ");
Console.WriteLine();
}
static void showDeq(Queue q)
{
Console.Write("Dequeue -
> ");
int a = (int) q.Dequeue();
Console.WriteLine(a);
Console.Write("queue: ");
foreach(int i in q)
Console.Write(i + " ");
Console.WriteLine();
}
public static void Main() {
Queue q = new Queue();
foreach(int i in q)
Console.Write(i + " ");
Console.WriteLine();
showEnq(q, 22);
showEnq(q, 65);
showEnq(q, 91);
showDeq(q);
showDeq(q);
showDeq(q);
try {
showDeq(q);
} catch (InvalidOperationException) {
Console.WriteLine("Queue empty.")
;
}
}
}