The document describes research on variable bit quantisation for locality sensitive hashing (LSH) to improve nearest neighbor search for large-scale applications. It discusses problems with existing single bit quantisation for LSH, such as high quantisation error. The proposed variable bit quantisation approach assigns bits differently to hyperplanes based on how well they preserve neighborhood structure. Evaluation on text and image retrieval tasks demonstrates substantial gains in retrieval accuracy compared to baseline methods.

1. Variable Bit Quantisation for Large Scale Search
Sean Moran
Final year PhD student
Institute of Language, Cognition and Computation
12th September 2014

2. Variable Bit Quantisation for Large Scale Search
Nearest Neighbour Search
Variable Bit Quantisation for LSH
Evaluation
Summary

3. Variable Bit Quantisation for Large Scale Search
Nearest Neighbour Search
Variable Bit Quantisation for LSH
Evaluation
Summary

4. Nearest Neighbour Search
I Given a query q

5. nd the nearest neighbour NN(q) from
X = fx1; x2 : : : ; xNg where NN(q) = argminx2Xdist(q; x)
I dist(q,x) is a distance measure - e.g. Euclidean, Cosine etc
q ?
y
1-NN
x
1-NN
q
x
y
I Generalised variant: K-nearest neighbour search (KNN(q))
I Compare query to all N database items - O(N) query time

6. Example: First Story Detection in Twitter
I Real-time detection of

7. rst stories in the Twitter stream
I Haiti earthquake struck 21:53,

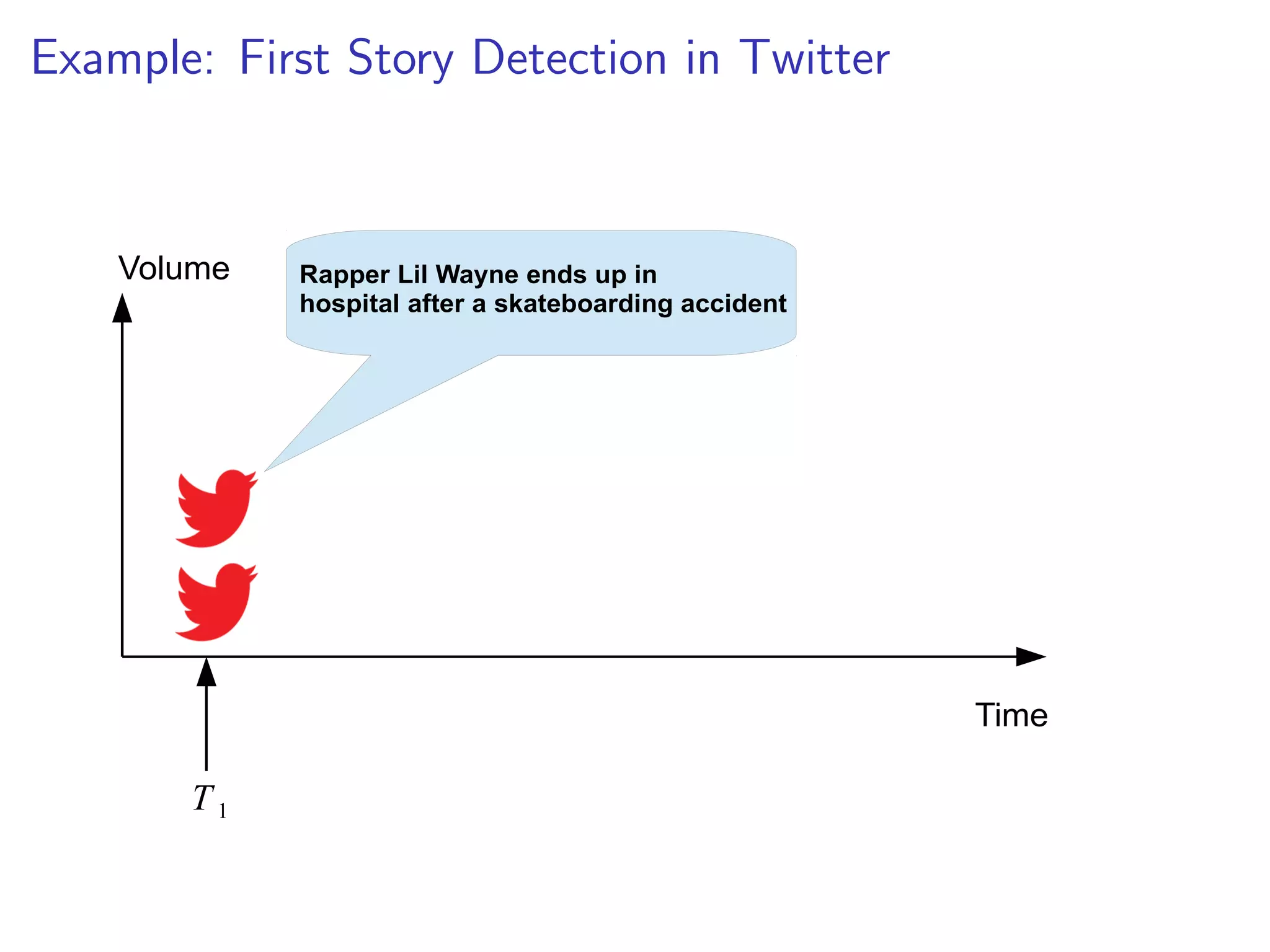
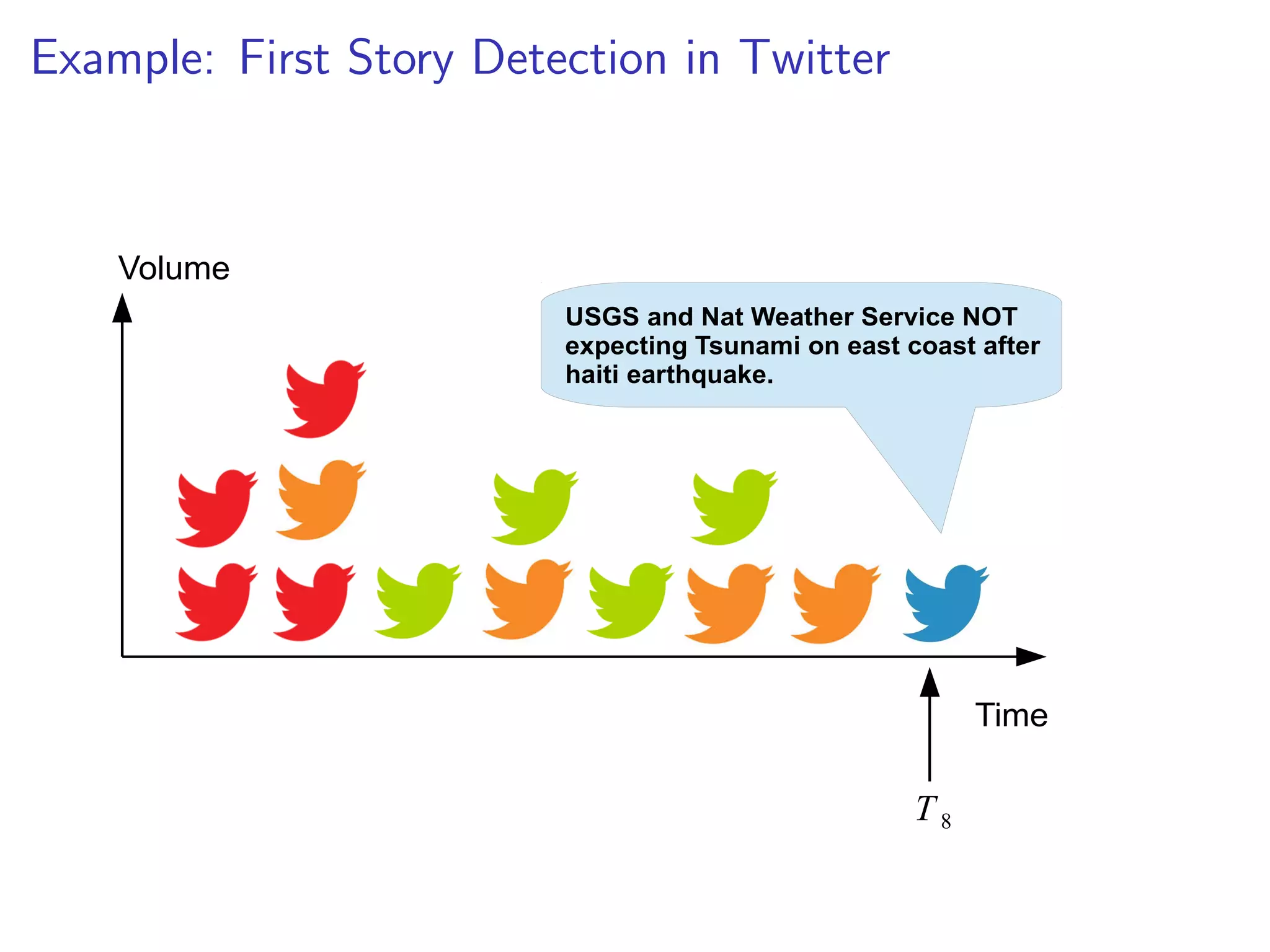
8. rst story at 22:17 UTC
I 22:17:43 justinholtweb NOT expecting Tsunami on east coast
after haiti earthquake. good news.
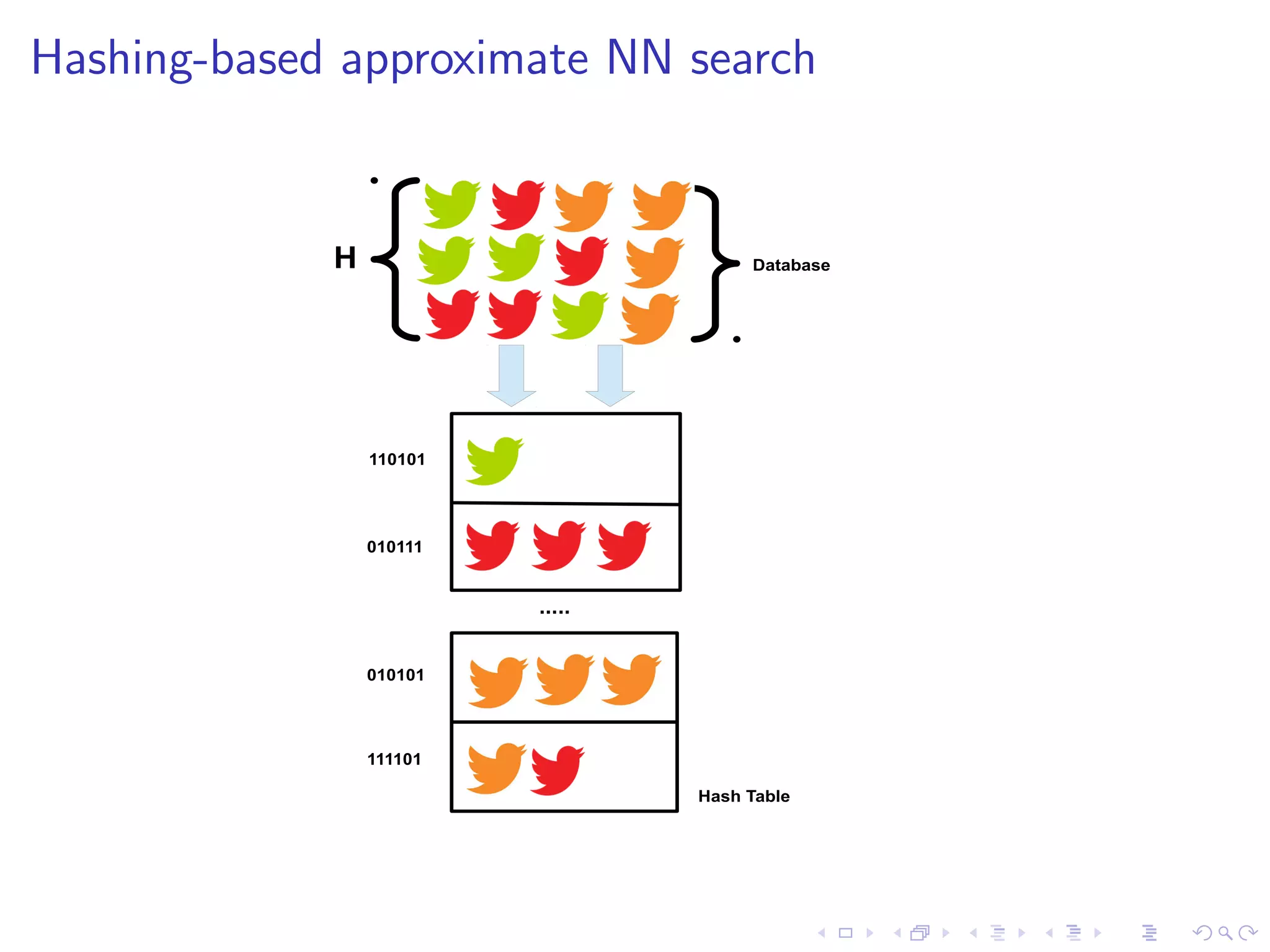
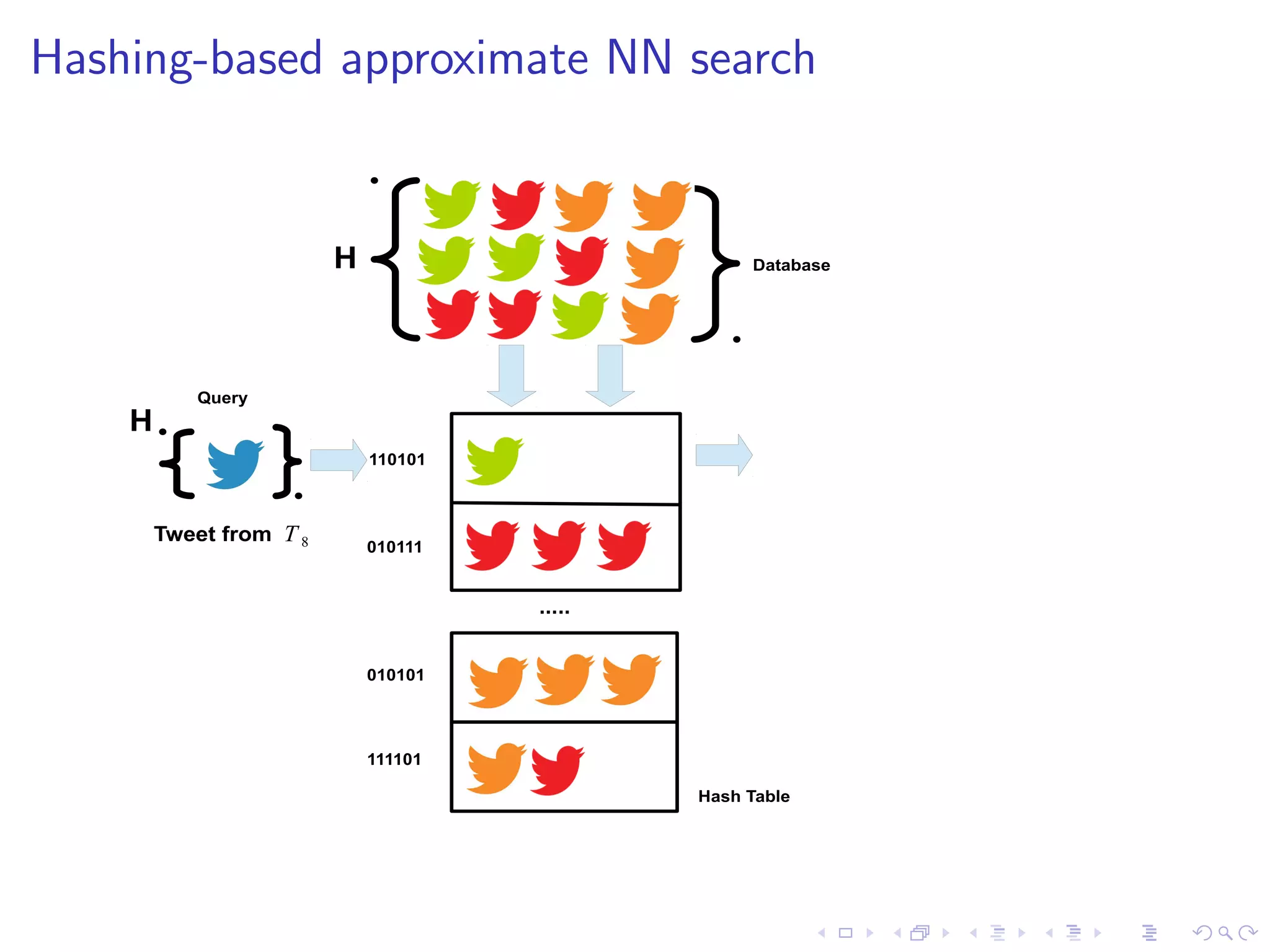
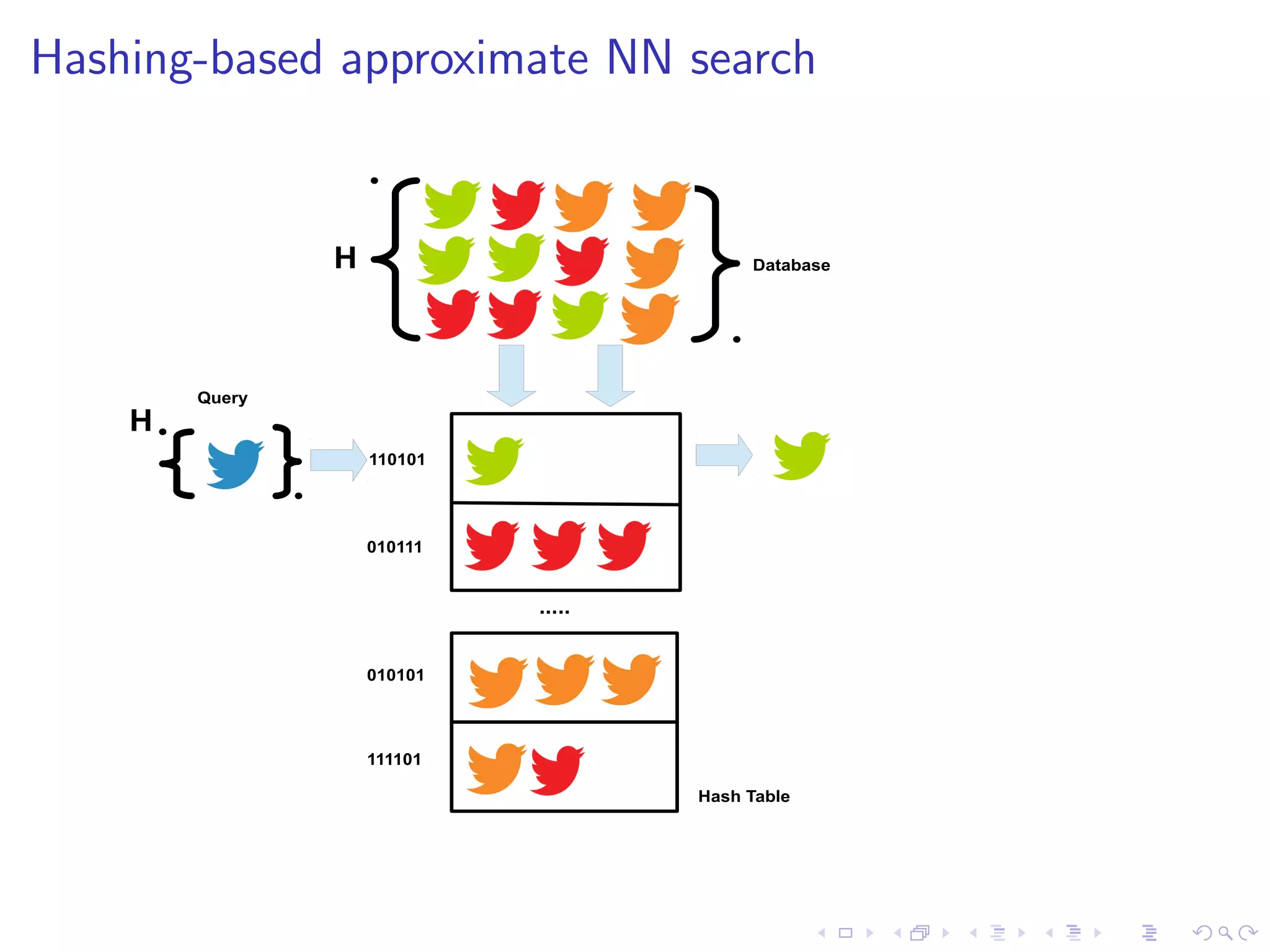
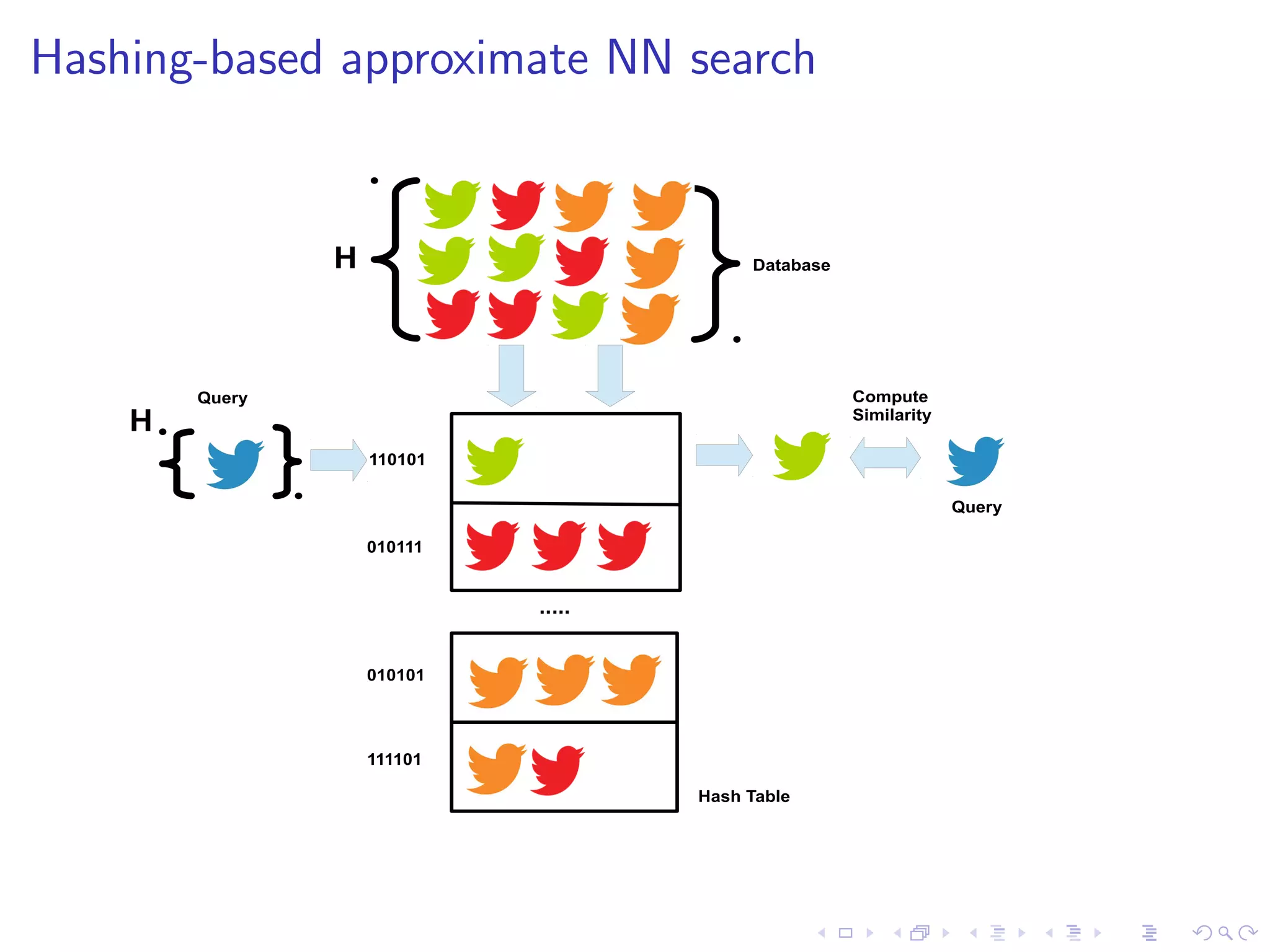
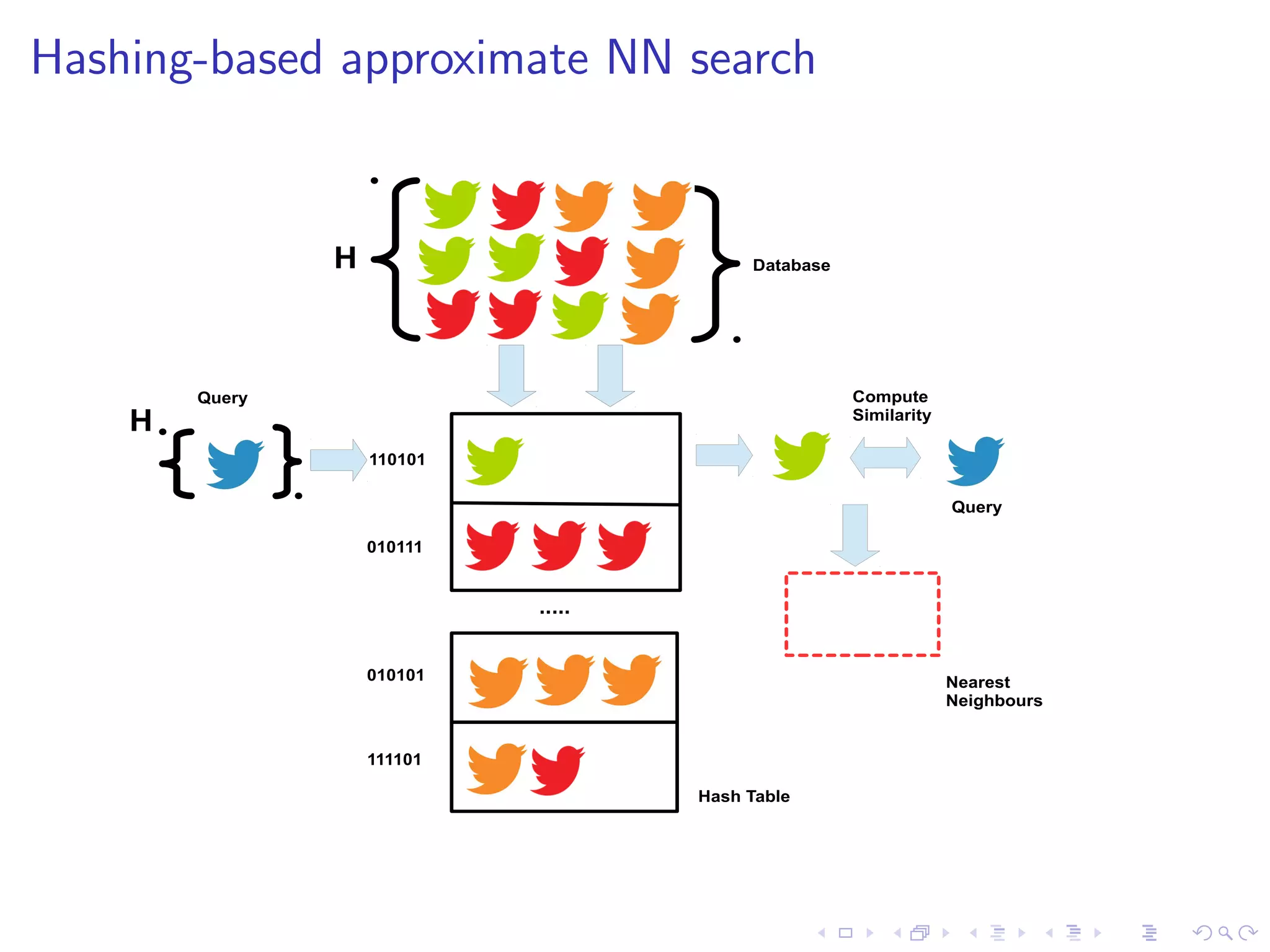
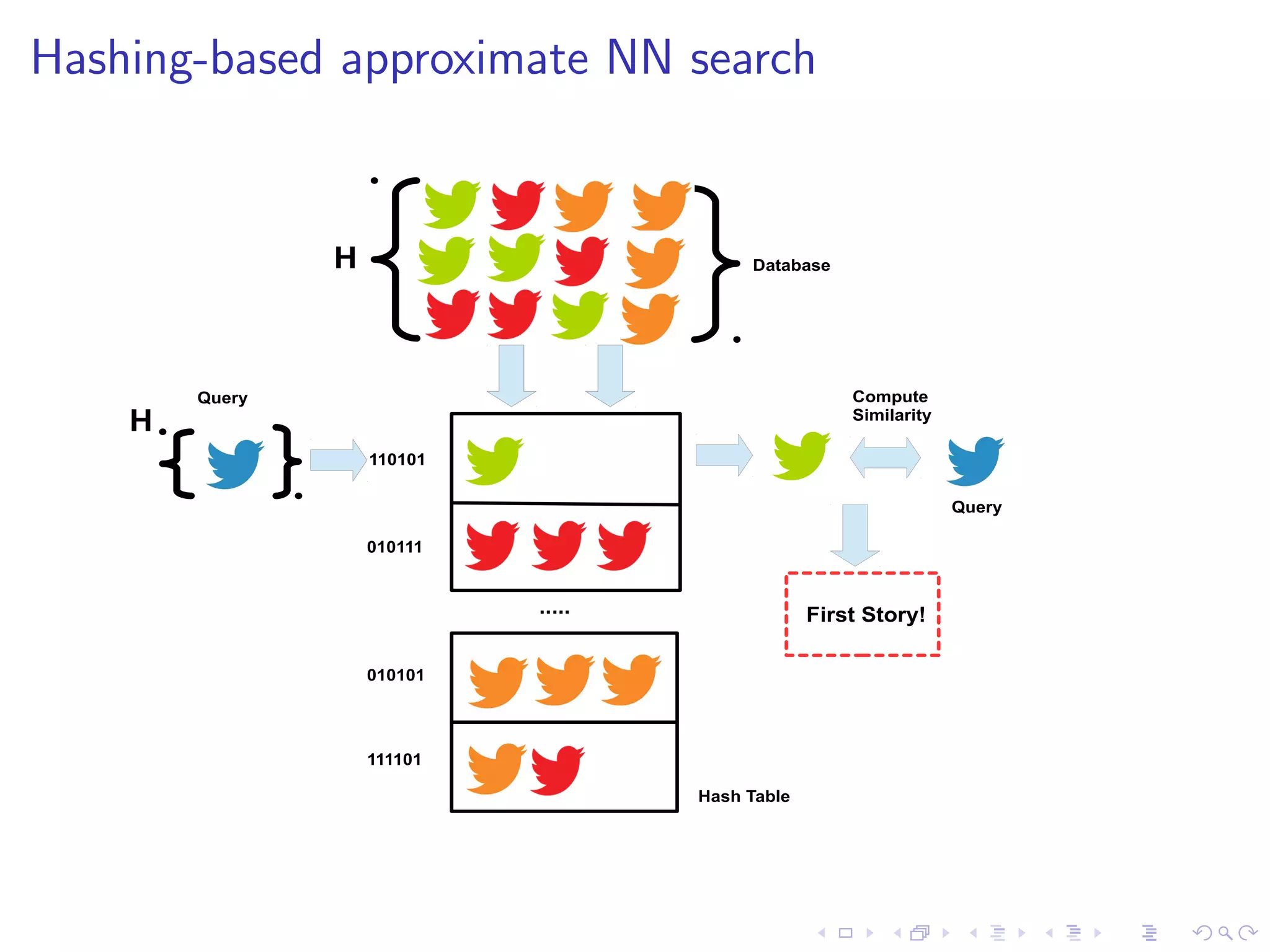
I State-of-the-art FSD uses NN search under the bonnet
I Problems: dimensionality (1 million+) and data volume
(250Gb/day)
I Hashing-based approximate NN operates in O(1) time [1]
[1] Real-Time Detection, Tracking and Monitoring of Discovered Events in
Social Media. S. Moran et al. In ACL'14.

9. Example: First Story Detection in Twitter
Time
Volume
T 1
Rapper Lil Wayne ends up in
hospital after a skateboarding accident

10. Example: First Story Detection in Twitter
Time
Thor Hushovd wins stage 13 of Tour de
France
T 2
Volume

11. Example: First Story Detection in Twitter
Time
T 3
Volume
Magnitude 5.4 earthquake hits western
Japan

12. Example: First Story Detection in Twitter
USGS and Nat Weather Service NOT
expecting Tsunami on east coast after
haiti earthquake.
Time
T 8
Volume

13. Hashing-based approximate NN search
H Database
Tweets from T 1 - T 7

14. Hashing-based approximate NN search
H Database
110101
010111
Hash Table
010101
111101
.....

15. Hashing-based approximate NN search
H
Query
Tweet from T 8
H Database
110101
010111
Hash Table
010101
111101
.....

16. Hashing-based approximate NN search
H
Query
H Database
110101
010111
Hash Table
010101
111101
.....

17. Hashing-based approximate NN search
H
Query Compute
Similarity
Query
H Database
110101
010111
010101
111101
.....
Hash Table

18. Hashing-based approximate NN search
H
Query
Nearest
Neighbours
H Database
110101
010111
010101
111101
.....
Compute
Similarity
Query
Hash Table

19. Hashing-based approximate NN search
H
Query
H Database
110101
010111
010101
111101
.....
Compute
Similarity
Query
First Story!
Hash Table

20. Locality Sensitive Hashing (LSH)
x
y

21. Locality Sensitive Hashing (LSH)
x
y
n2
n1
h1
h2
11
10
00 01

22. Locality Sensitive Hashing (LSH)
x
y
h1(q) h2(q)
q
n2
n1
h1
h2
11
10
00 01

23. Step 1: Projection
n2
n1
q

24. Step 2: Single Bit Quantisation (SBQ)
t
0 1
n2
q
I Threshold typically zero (sign function): sgn(n2:q)
I Generate full 2 bit hash key (bitcode) by concatenation:
g(q) = h1(q) h2(q) = sgn(n1:q) sgn(n2:q)
= 1 1 = 11

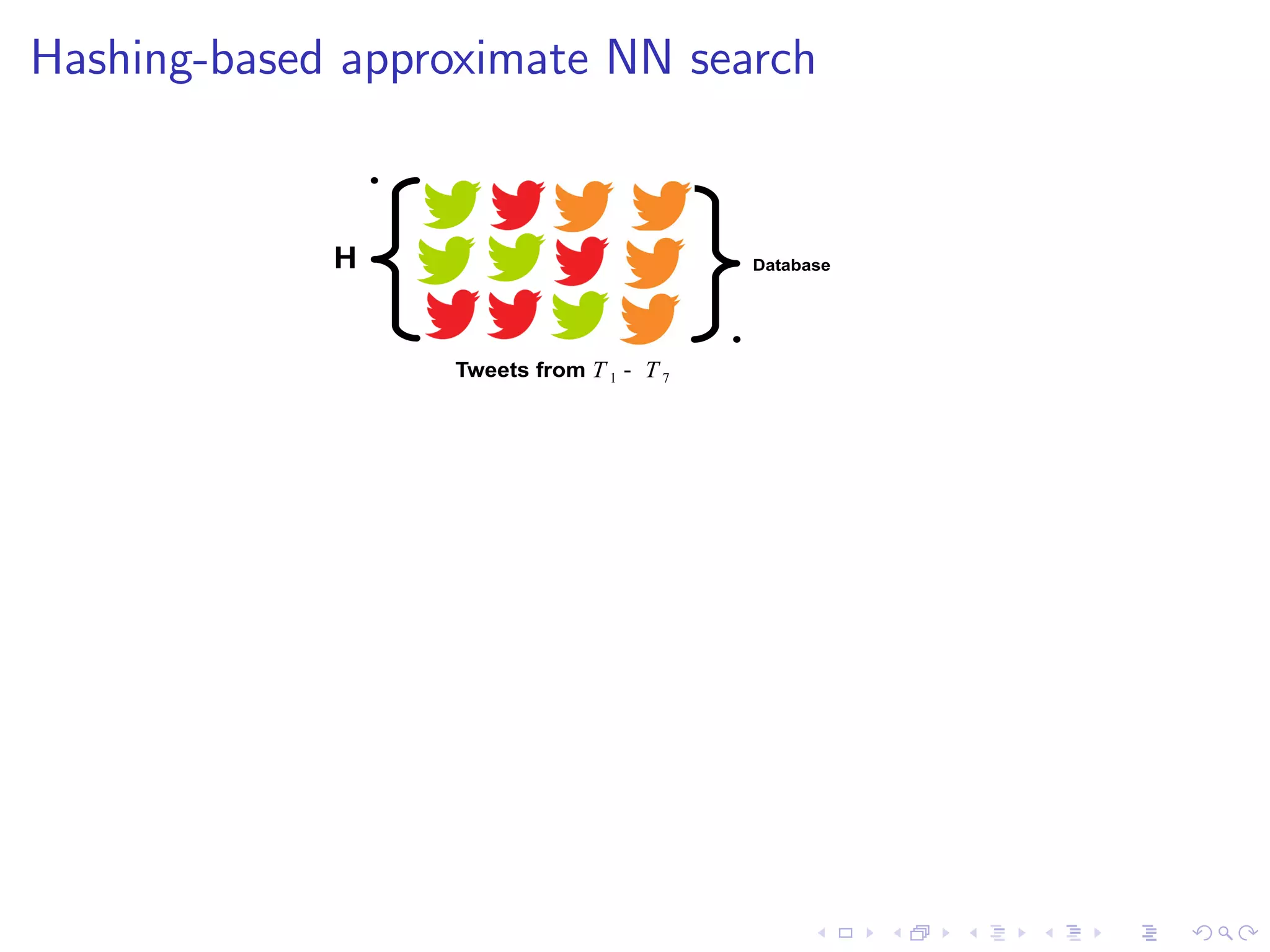
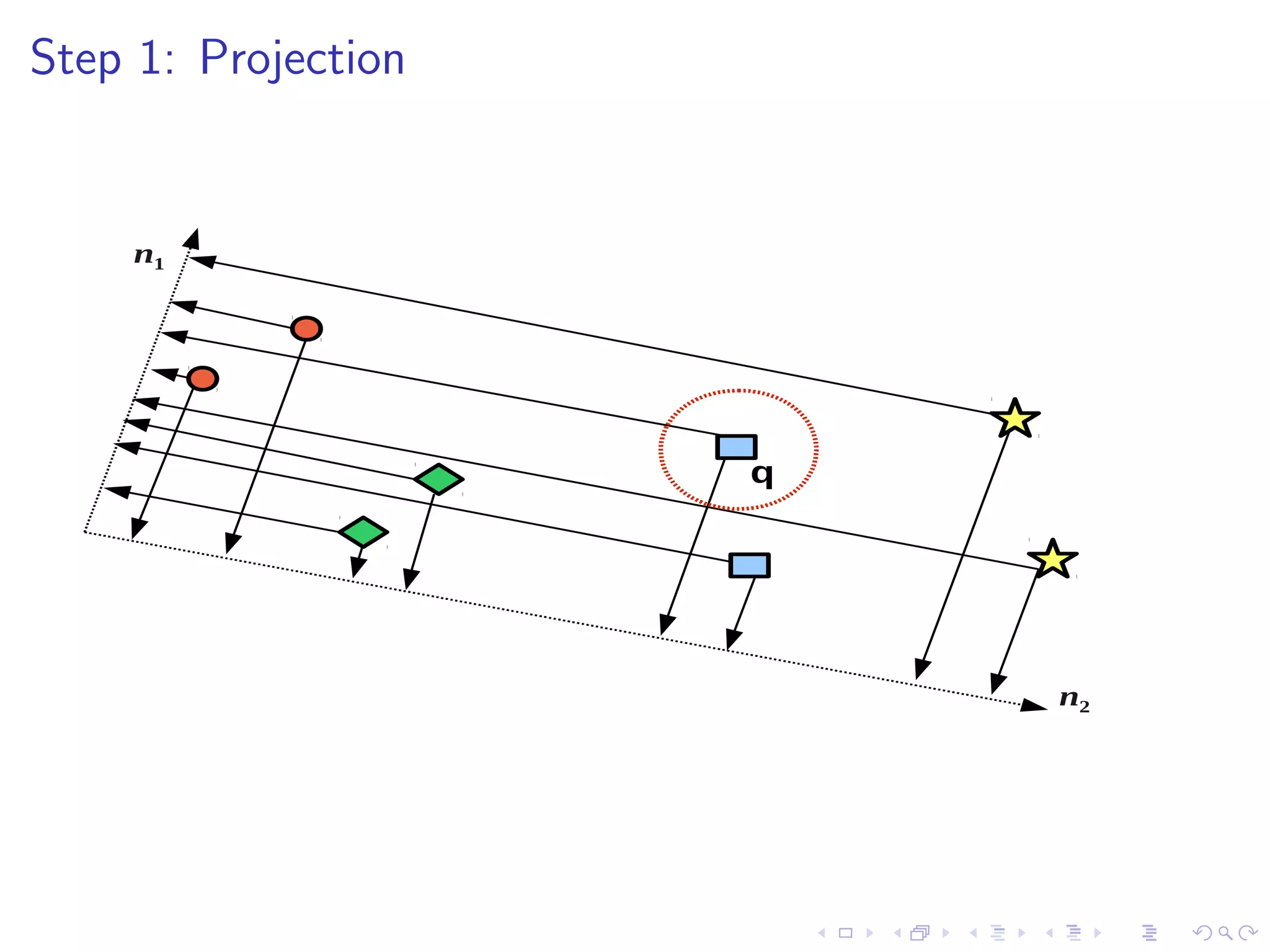
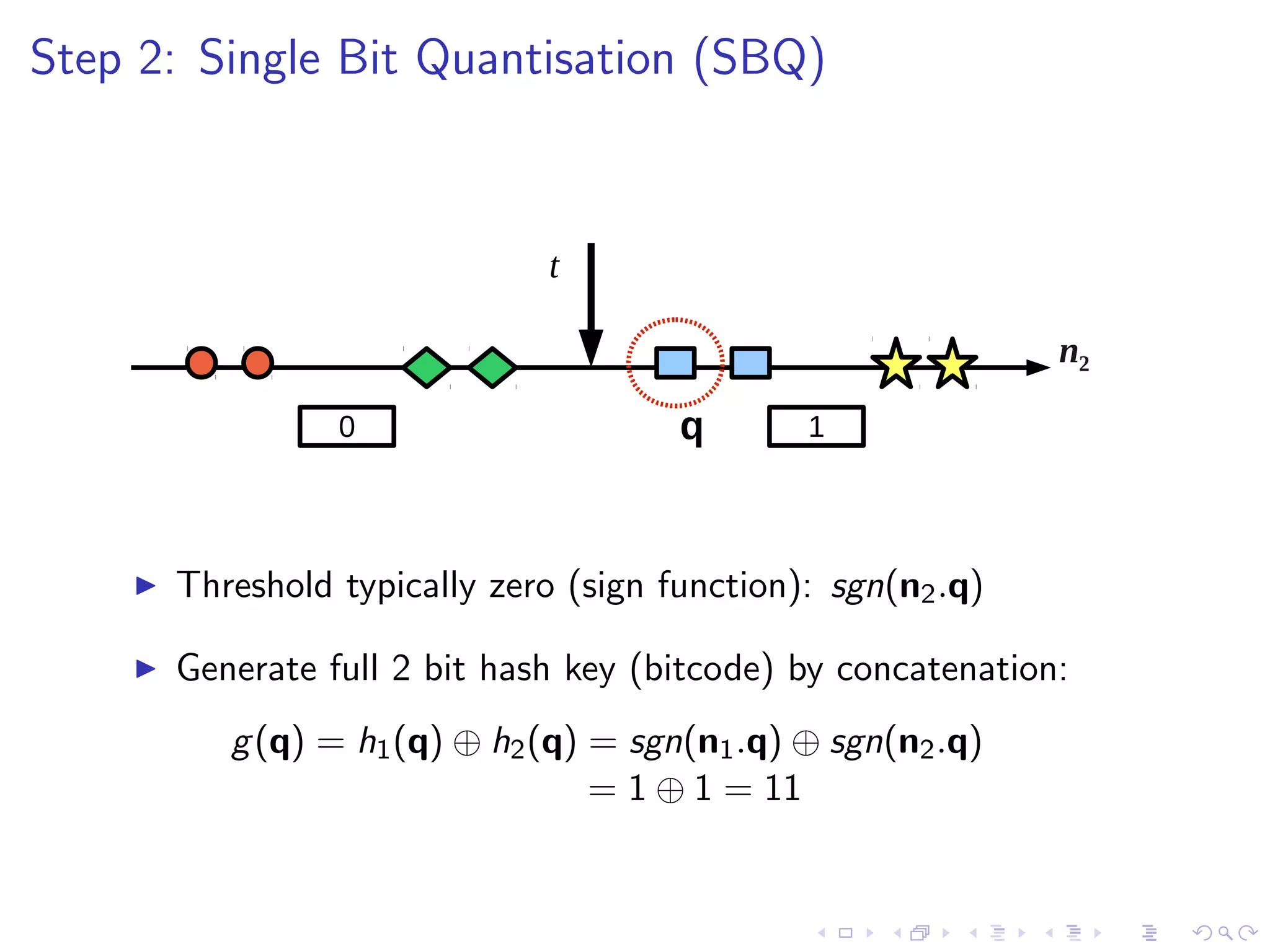
25. Many more methods exist...
I Very active area of research:
I Kernel methods [3]
I Spectral methods [4] [5]
I Neural networks [6]
I Loss based methods [7]
I Commonality: all use single bit quantisation (SBQ)
[3] M. Raginsky and S. Lazebnik. Locality-sensitive binary codes from shift-invariant kernels. In NIPS '09.
[4] Y. Weiss and A. Torralba and R. Fergus. Spectral Hashing. NIPS '08.
[5] J. Wang and S. Kumar and SF. Chang. Semi-supervised hashing for large-scale search. PAMI '12.
[6] R. Salakhutdinov and G. Hinton. Semantic Hashing. NIPS '08.
[7] B. Kulis and T. Darrell. Learning to Hash with Binary Reconstructive Embeddings. NIPS '09.

26. Variable Bit Quantisation for Large Scale Search
Nearest Neighbour Search
Variable Bit Quantisation for LSH
Evaluation
Summary

27. Problem 1: SBQ leads to high quantisation errors
I Threshold at zero can separate many related Tweets:
6000
5000
4000
3000
2000
1000
0
−1.5 −1 −0.5 0 0.5 1 1.5
Projected Value
Count

28. Problem 2: some hyperplanes are better than others
10
Projected Dimension 2 n2
n1
Projected Dimension 1
x
y
n2
n1
h1
h2
11
00 01

29. Problem 2: some hyperplanes are better than others
10
Projected Dimension 2 n2
n1
Projected Dimension 1
x
y
n2
n1
h1
h2
11
00 01

30. Problem 2: some hyperplanes are better than others
10
Projected Dimension 2 n2
n1
Projected Dimension 1
x
y
n2
n1
h1
h2
11
00 01

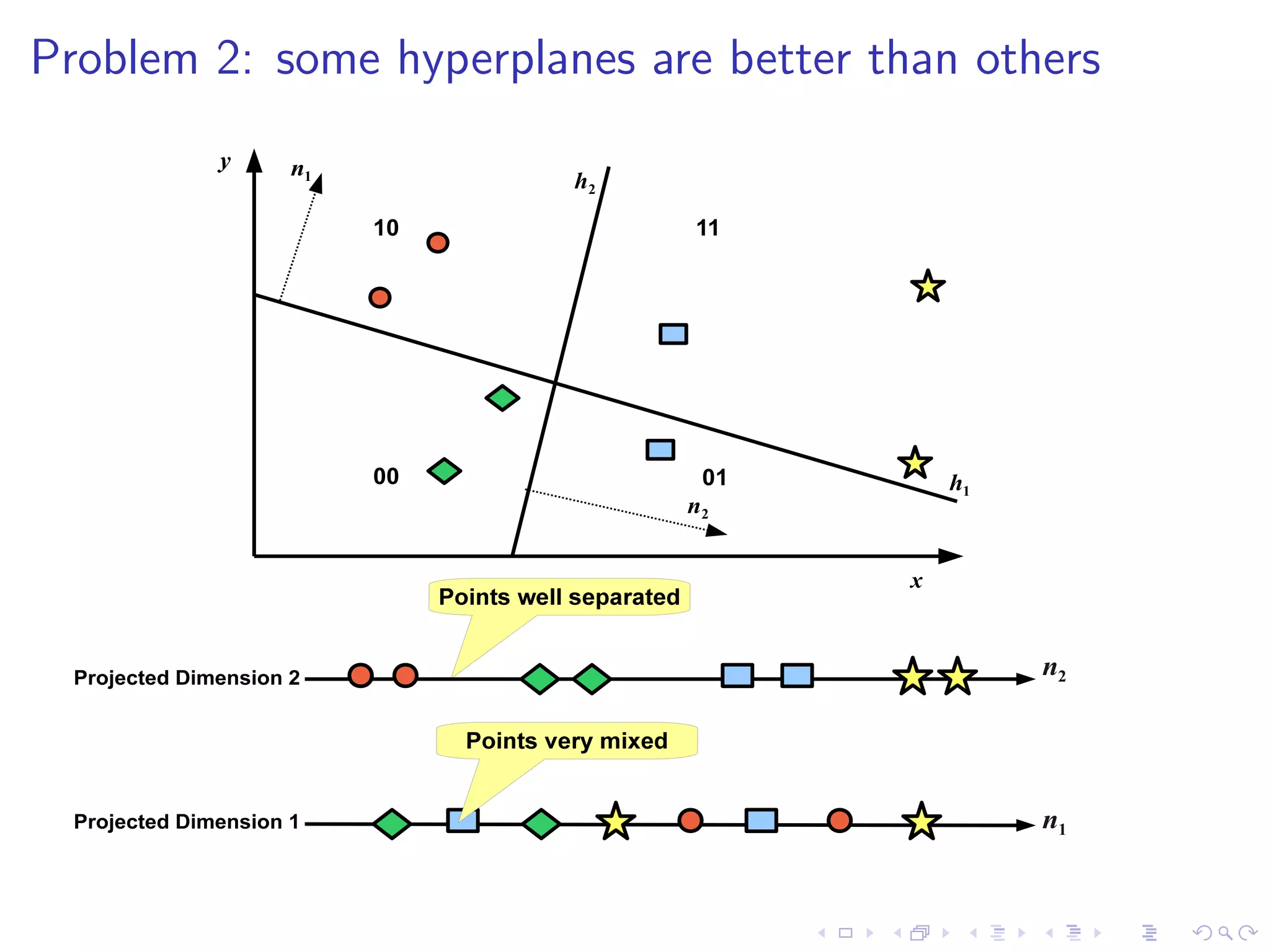
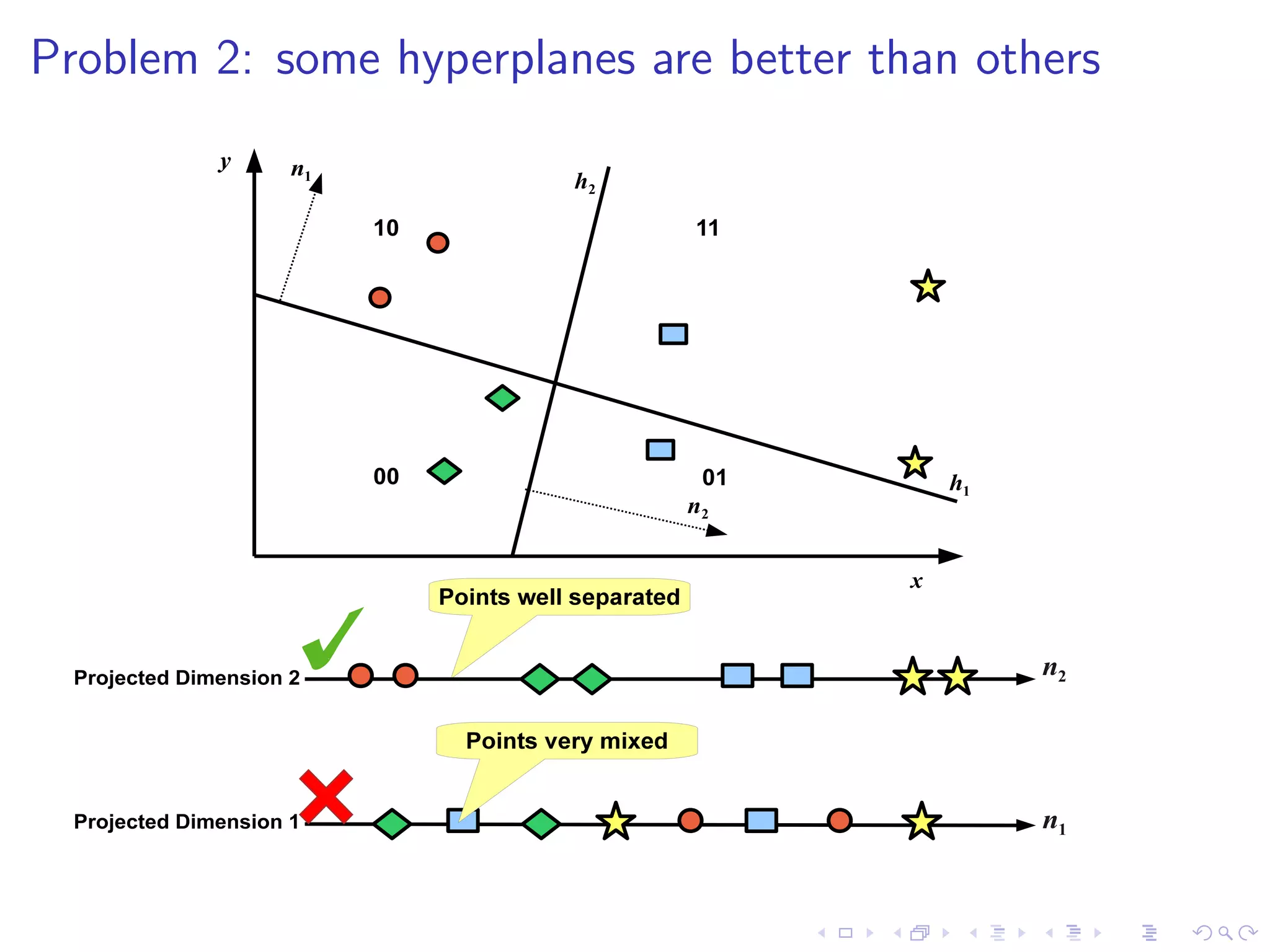
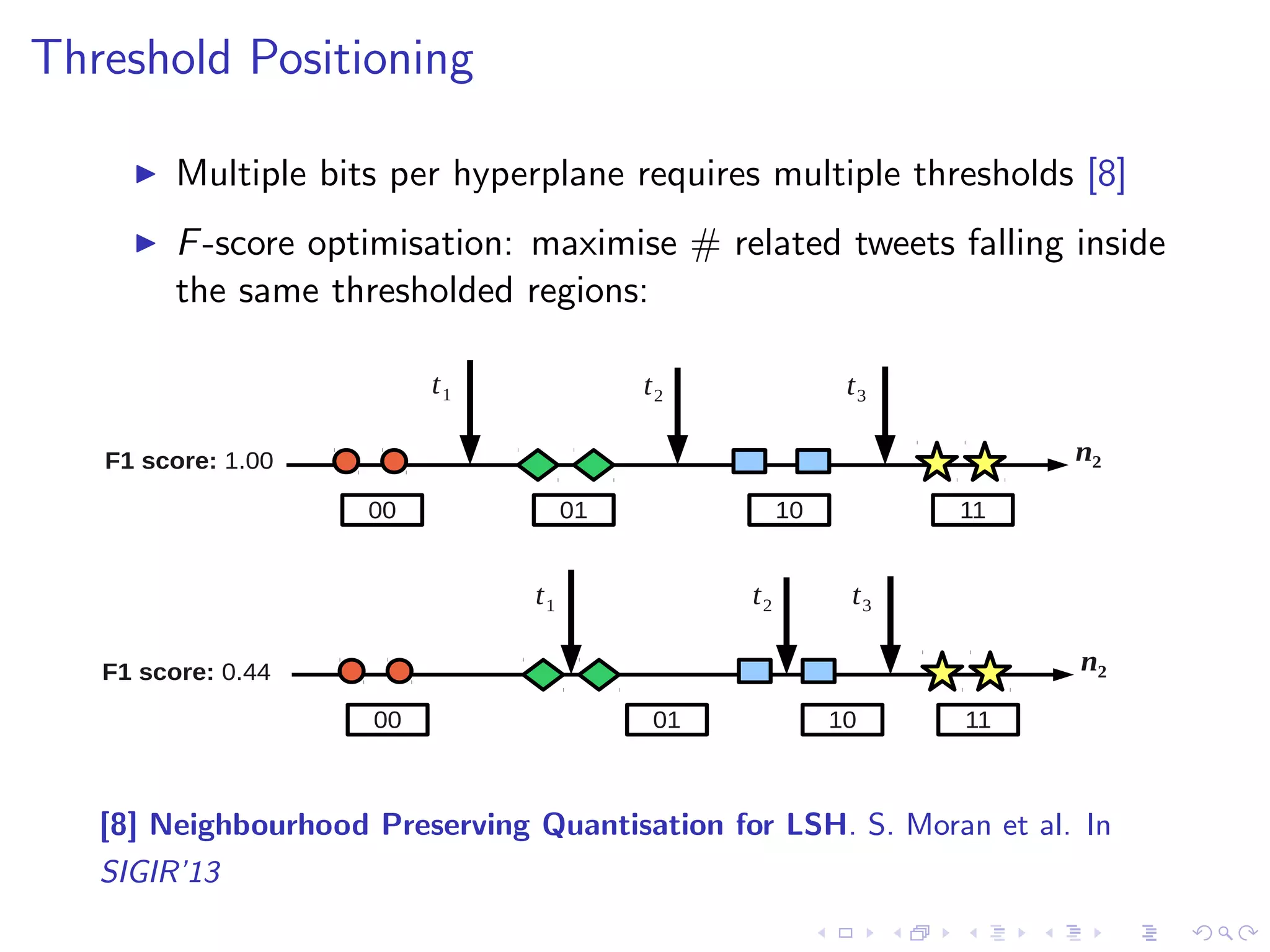
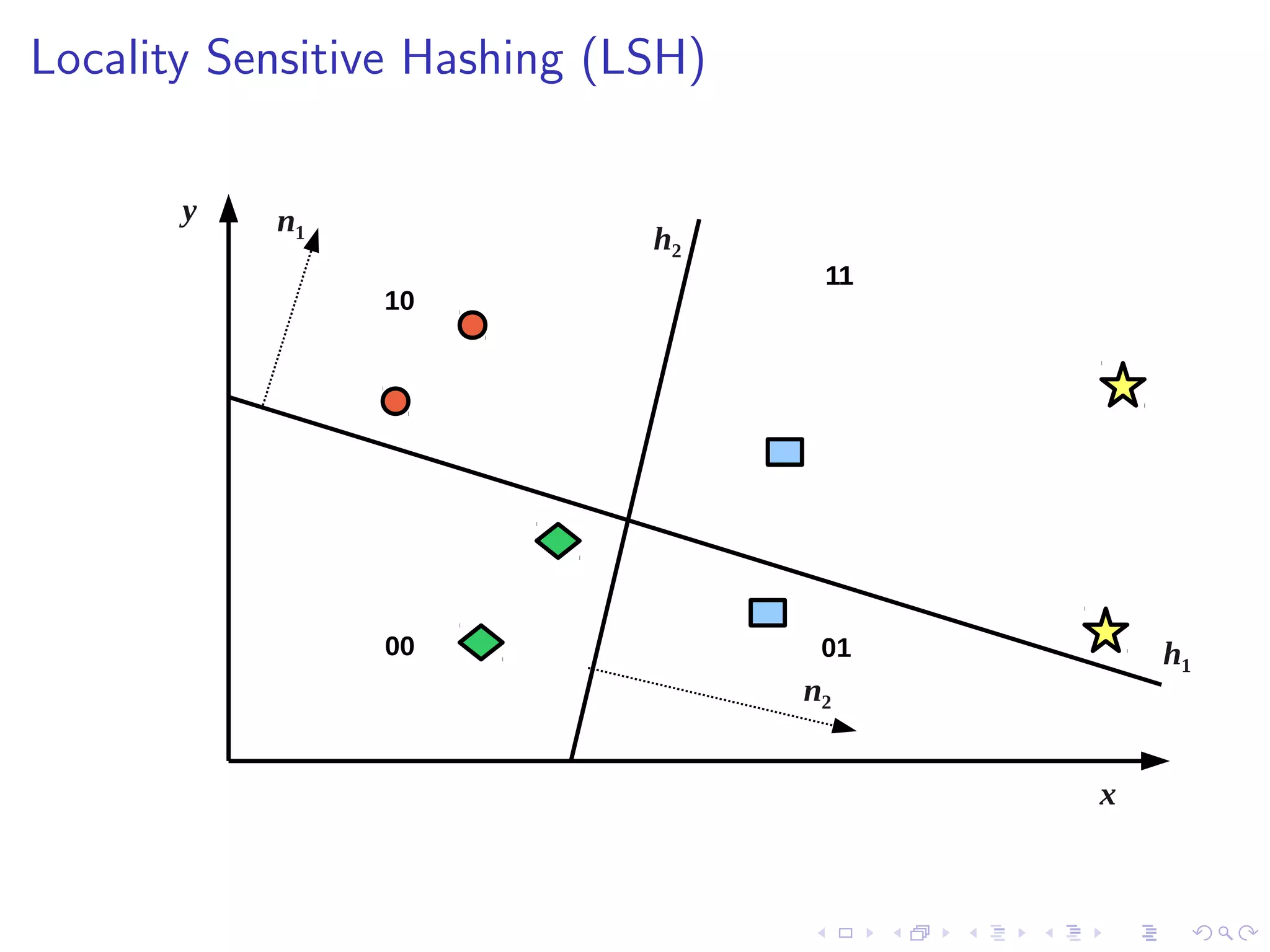
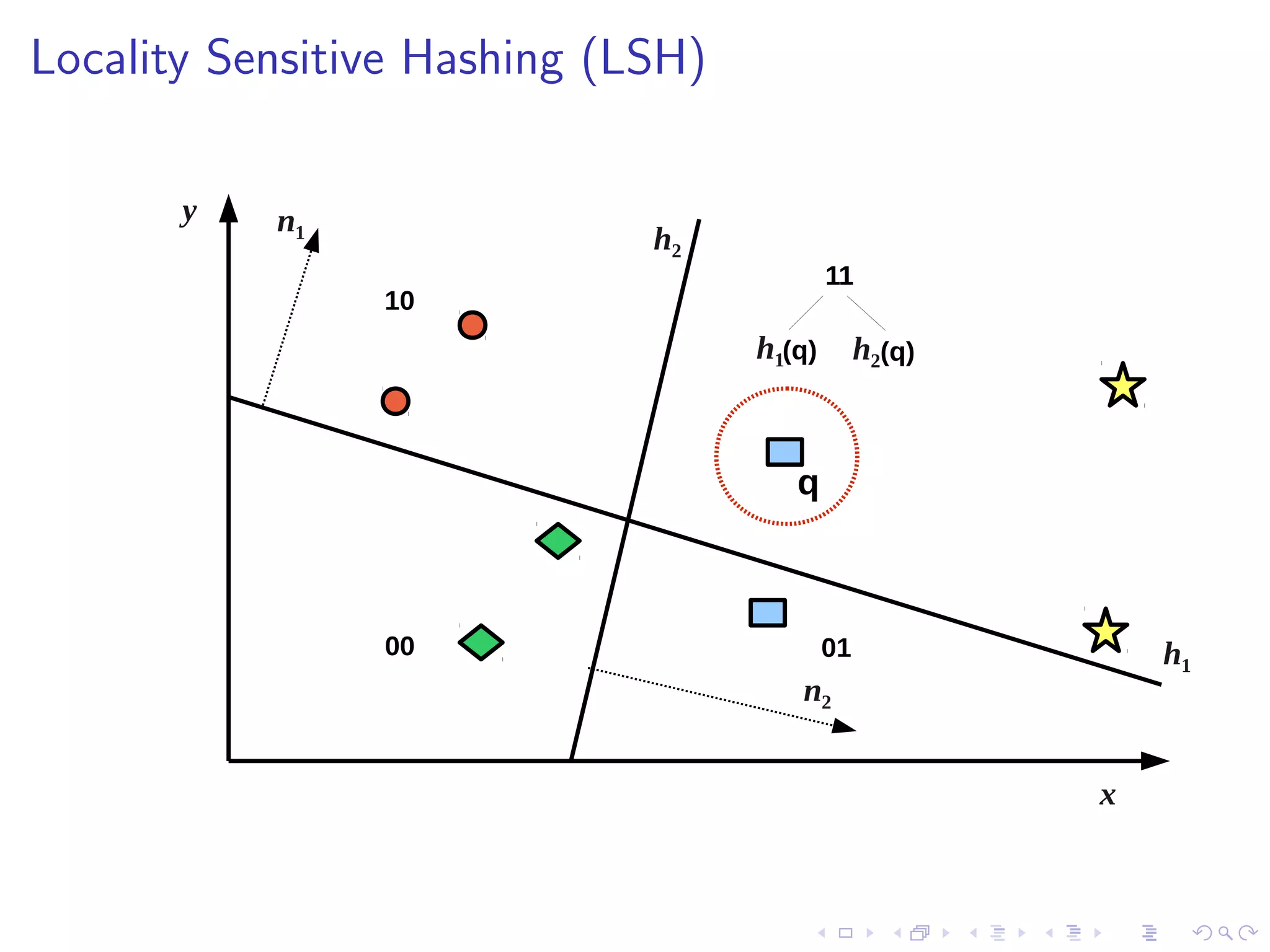
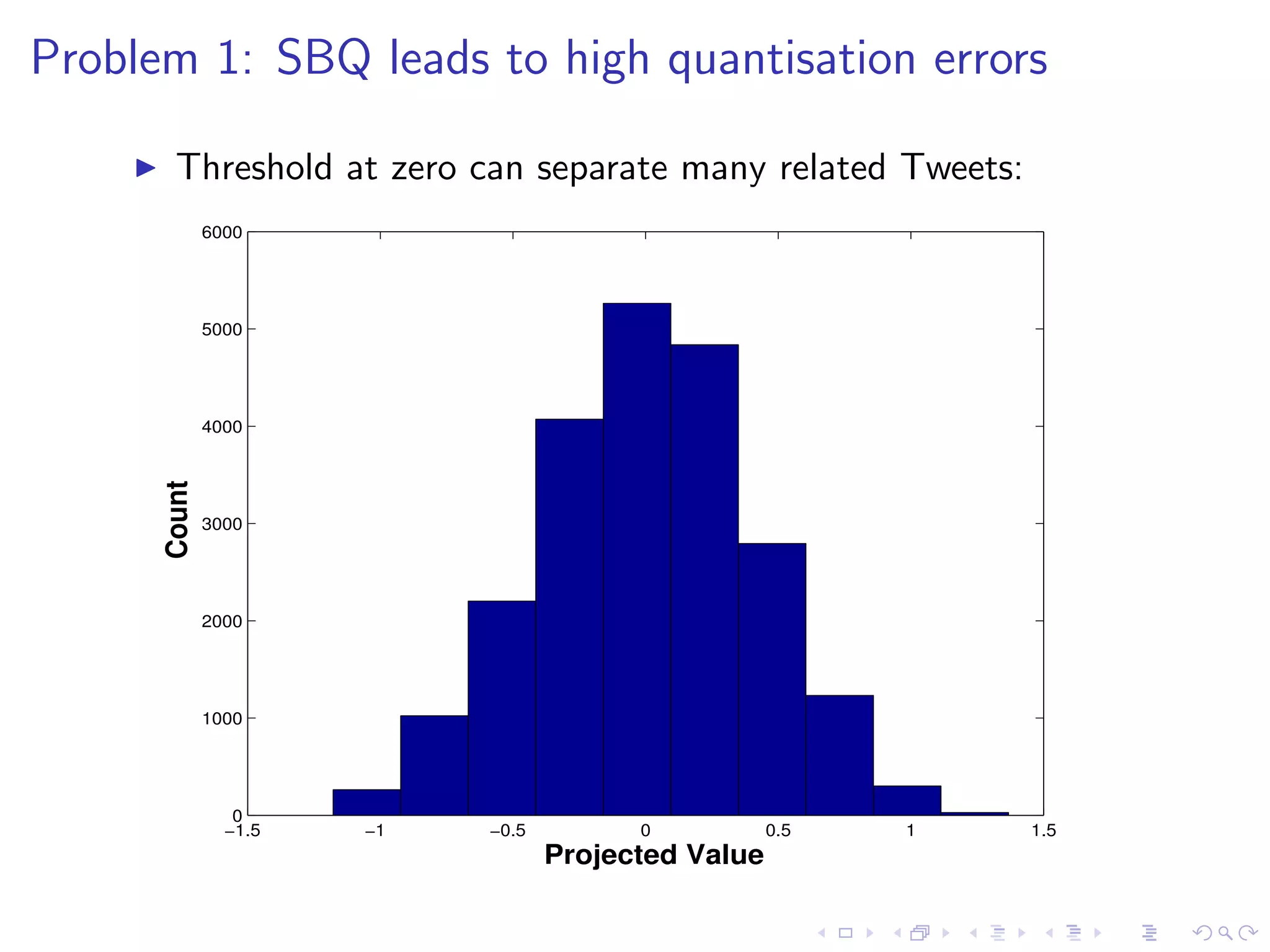
31. Threshold Positioning
I Multiple bits per hyperplane requires multiple thresholds [8]
I F-score optimisation: maximise # related tweets falling inside
the same thresholded regions:
F1 score: 1.00
t1 t2 t3
00 01 10 11
n2
F1 score: 0.44
t1 t2 t3
00 01 10 11
n2
[8] Neighbourhood Preserving Quantisation for LSH. S. Moran et al. In
SIGIR'13

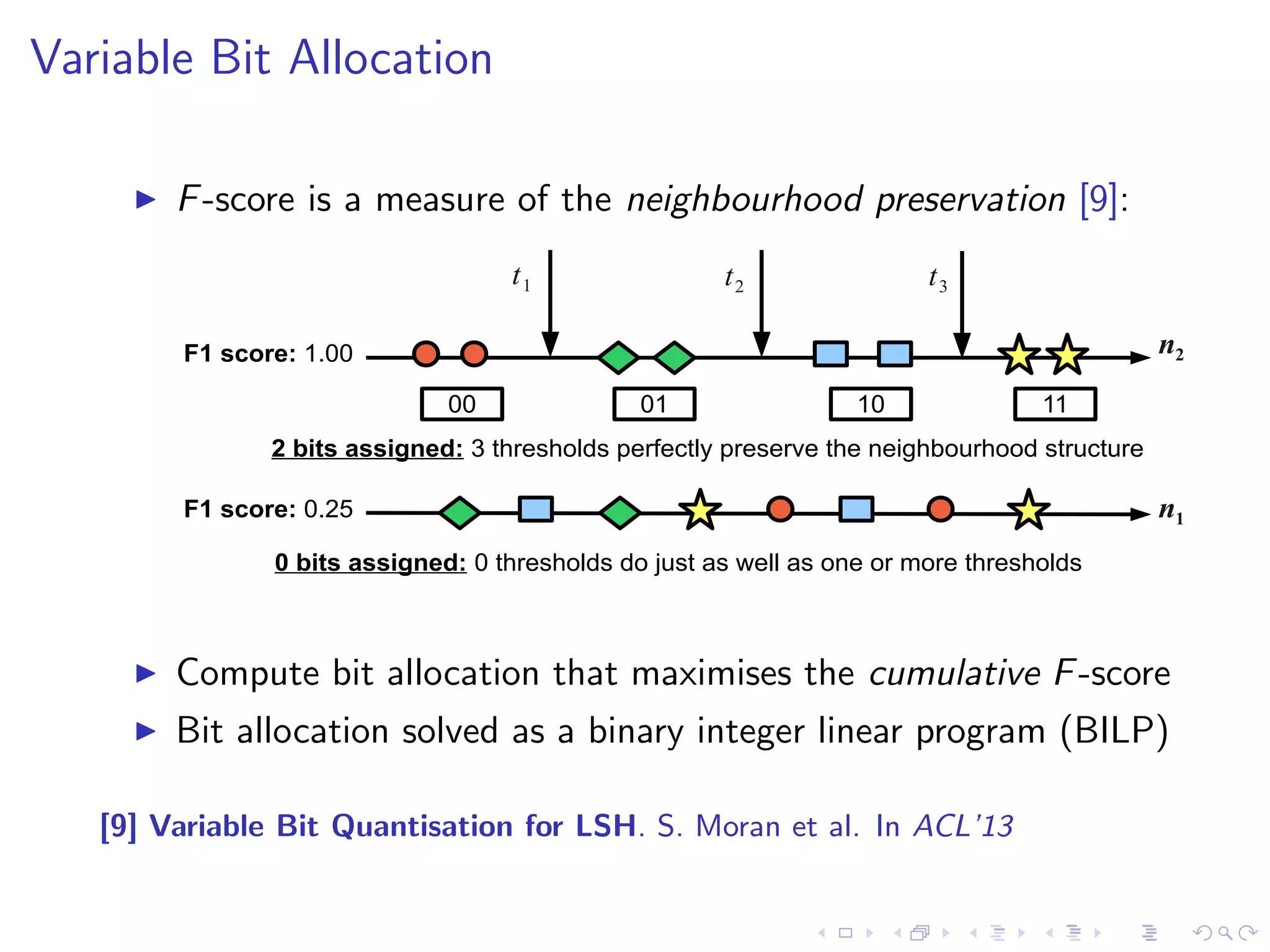
32. Variable Bit Allocation
I F-score is a measure of the neighbourhood preservation [9]:
F1 score: 1.00
F1 score: 0.25
t1 t2 t3
00 01 10 11
0 bits assigned: 0 thresholds do just as well as one or more thresholds
n2
n1
2 bits assigned: 3 thresholds perfectly preserve the neighbourhood structure
I Compute bit allocation that maximises the cumulative F-score
I Bit allocation solved as a binary integer linear program (BILP)
[9] Variable Bit Quantisation for LSH. S. Moran et al. In ACL'13

33. Variable Bit Allocation
max kF Zk
subject to kZhk = 1 h 2 f1 : : : Bg
kZ Dk B
Z is binary
I F contains the F scores per hyperplane, per bit count
I Z is an indicator matrix specifying the bit allocation
I D is a constraint matrix
I B is the bit budget
I k:k denotes the Frobenius L1 norm
I the Hadamard product
[9] Variable Bit Quantisation for LSH. S. Moran et al. In ACL'13

34. Variable Bit Allocation
max kF Zk
subject to kZhk = 1 h 2 f1 : : : Bg
kZ Dk B
Z is binary
I F contains the F scores per hyperplane, per bit count
I Z is an indicator matrix specifying the bit allocation
I D is a constraint matrix
I B is the bit budget
I k:k denotes the Frobenius L1 norm
I the Hadamard product
[9] Variable Bit Quantisation for LSH. S. Moran et al. In ACL'13

35. Variable Bit Allocation
max kF Zk
subject to kZhk = 1 h 2 f1 : : : Bg
kZ Dk B
Z is binary
I F contains the F scores per hyperplane, per bit count
I Z is an indicator matrix specifying the bit allocation
I D is a constraint matrix
I B is the bit budget
I k:k denotes the Frobenius L1 norm
I the Hadamard product
[9] Variable Bit Quantisation for LSH. S. Moran et al. In ACL'13

36. Variable Bit Allocation
max kF Zk
subject to kZhk = 1 h 2 f1 : : : Bg
kZ Dk B
Z is binary
I F contains the F scores per hyperplane, per bit count
I Z is an indicator matrix specifying the bit allocation
I D is a constraint matrix
I B is the bit budget
I k:k denotes the Frobenius L1 norm
I the Hadamard product
[9] Variable Bit Quantisation for LSH. S. Moran et al. In ACL'13

37. Variable Bit Allocation
max kF Zk
subject to kZhk = 1 h 2 f1 : : : Bg
kZ Dk B
Z is binary
F 0
h1 h2
b0 0:25 0:25
b1 @
0:35 0:50
b2 0:40 1:00
1
A
0
@
D
0 0
1 1
2 2
1
A
0
@
Z
1 0
0 0
0 1
1
A
I Sparse solution: lower quality hyperplanes discarded [9].
[9] Variable Bit Quantisation for LSH. S. Moran et al. In ACL'13

38. Variable Bit Quantisation for Large Scale Search
Nearest Neighbour Search
Variable Bit Quantisation for LSH
Evaluation
Summary

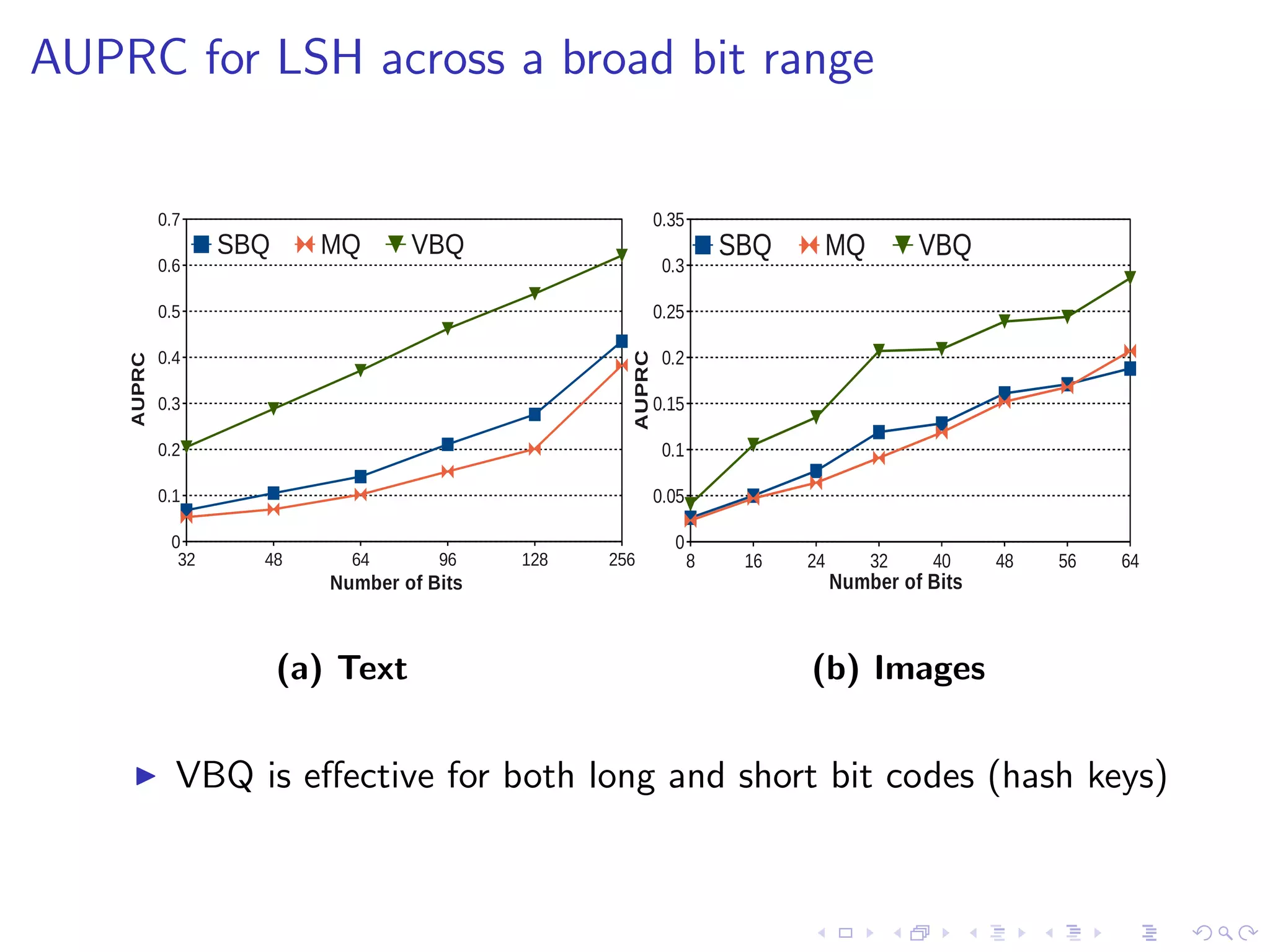
39. Evaluation Protocol
I Task: Text and image retrieval
I Projections: LSH [2], Shift-invariant kernel hashing (SIKH)
[3], Spectral Hashing (SH) [4] and PCA-Hashing (PCAH) [5].
I Baselines: Single Bit Quantisation (SBQ), Manhattan
Hashing (MQ)[10], Double-Bit quantisation (DBQ) [11].
I Evaluation: how well do we retrieve the NN of queries?
[2] P. Indyk and R. Motwani. Approximate nearest neighbors: removing the curse of dimensionality. In STOC '98.
[3] M. Raginsky and S. Lazebnik. Locality-sensitive binary codes from shift-invariant kernels. In NIPS '09.
[4] Y. Weiss and A. Torralba and R. Fergus. Spectral Hashing. NIPS '08.
[9] J. Wang and S. Kumar and SF. Chang. Semi-supervised hashing for large-scale search. PAMI '12.
[10] W. Kong and W. Li and M. Guo. Manhattan hashing for large-scale image retrieval. SIGIR '12.
[11] W. Kong and W. Li. Double Bit Quantisation for Hashing. AAAI '12.

40. AUPRC across dierent projections (variable # bits)
Dataset Images (32 bits) Text (128 bits)
SBQ MQ DBQ VBQ SBQ MQ DBQ VBQ
SIKH 0.042 0.046 0.047 0.161 0.102 0.112 0.087 0.389
LSH 0.119 0.091 0.066 0.207 0.276 0.201 0.175 0.538
SH 0.051 0.144 0.111 0.202 0.033 0.028 0.030 0.154
PCAH 0.036 0.132 0.107 0.219 0.095 0.034 0.027 0.154
I Variable bit allocation yields substantial gains in retrieval
accuracy
I VBQ is an eective multimodal quantisation scheme

41. AUPRC for LSH across a broad bit range
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
SBQ MQ VBQ
32 48 64 96 128 256
Number of Bits
AUPRC
8 16 24 32 40 48 56 64
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
SBQ MQ VBQ
Number of Bits
AUPRC
(a) Text (b) Images
I VBQ is eective for both long and short bit codes (hash keys)

42. Variable Bit Quantisation for Large Scale Search
Nearest Neighbour Search
Variable Bit Quantisation for LSH
Evaluation
Summary

43. Summary
I Proposed a novel data-driven scheme (VBQ) to adaptively
assign variable bits per LSH hyperplane
I Hyperplanes better preserving the neighbourhood structure
are aorded more bits from budget
I VBQ substantially increased LSH retrieval performance across
text and image datasets
I Current work: method to couple the quantisation and
projection stages of LSH

44. Thank you for your attention!
I FSD live system: goo.gl/Q7WQOk [1]
I Running over live Twitter stream in real time
I Sub-second detection latency via ANN search (1 CPU!)
I Papers: www.seanjmoran.com [1][8][9]
I Contact: sean.moran@ed.ac.uk
[1] Real-Time Detection, Tracking and Monitoring of Discovered Events in
Social Media. S. Moran et al. In ACL'14.
[8] Variable Bit Quantisation for LSH. S. Moran et al. In ACL'13
[9] Neighbourhood Preserving Quantisation for LSH. S. Moran et al. In
SIGIR'13