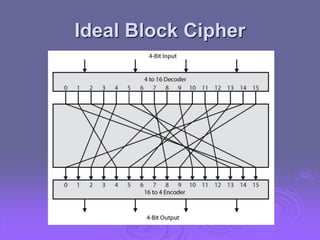
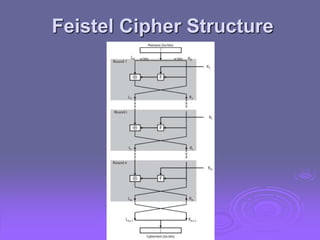
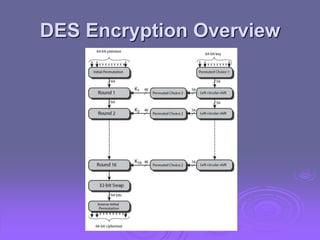
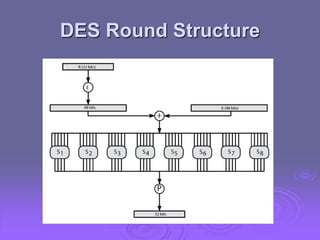
This document discusses block ciphers and the Data Encryption Standard (DES) by exploring their fundamental principles, structures, and historical context. It highlights the significance of Feistel ciphers, confusion and diffusion concepts, and various attack methodologies such as differential and linear cryptanalysis. The document also addresses the controversies surrounding the design of DES, particularly regarding key size and security implications.

1. Cryptography and
Network Security
Chapter 3
Fourth Edition
by William Stallings
Lecture slides by Lawrie Brown

2. Chapter 3 – Block Ciphers and
the Data Encryption Standard
All the afternoon Mungo had been working on
Stern's code, principally with the aid of the latest
messages which he had copied down at the
Nevin Square drop. Stern was very confident.
He must be well aware London Central knew
about that drop. It was obvious that they didn't
care how often Mungo read their messages, so
confident were they in the impenetrability of the
code.
—Talking to Strange Men, Ruth Rendell

3. Modern Block Ciphers
 now look at modern block ciphers
 one of the most widely used types of
cryptographic algorithms
 provide secrecy /authentication services
 focus on DES (Data Encryption Standard)
 to illustrate block cipher design principles

4. Block vs Stream Ciphers
 block ciphers process messages in blocks,
each of which is then en/decrypted
 like a substitution on very big characters
 64-bits or more
 stream ciphers process messages a bit or
byte at a time when en/decrypting
 many current ciphers are block ciphers
 broader range of applications

5. Block Cipher Principles
 most symmetric block ciphers are based on a
Feistel Cipher Structure
 needed since must be able to decrypt ciphertext
to recover messages efficiently
 block ciphers look like an extremely large
substitution
 would need table of 264 entries for a 64-bit block
 instead create from smaller building blocks
 using idea of a product cipher

6. Ideal Block Cipher

7. Claude Shannon and Substitution-
Permutation Ciphers
 Claude Shannon introduced idea of substitution-
permutation (S-P) networks in 1949 paper
 form basis of modern block ciphers
 S-P nets are based on the two primitive
cryptographic operations seen before:
 substitution (S-box)
 permutation (P-box)
 provide confusion & diffusion of message & key

8. Confusion and Diffusion
 cipher needs to completely obscure
statistical properties of original message
 a one-time pad does this
 more practically Shannon suggested
combining S & P elements to obtain:
 diffusion – dissipates statistical structure
of plaintext over bulk of ciphertext
 confusion – makes relationship between
ciphertext and key as complex as possible

9. Feistel Cipher Structure
 Horst Feistel devised the feistel cipher
 based on concept of invertible product cipher
 partitions input block into two halves
 process through multiple rounds which
 perform a substitution on left data half
 based on round function of right half & subkey
 then have permutation swapping halves
 implements Shannon’s S-P net concept

10. Feistel Cipher Structure

11. Feistel Cipher Design Elements
 block size
 key size
 number of rounds
 subkey generation algorithm
 round function
 fast software en/decryption
 ease of analysis

12. Feistel Cipher Decryption

13. Data Encryption Standard (DES)
 most widely used block cipher in world
 adopted in 1977 by NBS (now NIST)
 as FIPS PUB 46
 encrypts 64-bit data using 56-bit key
 has widespread use
 has been considerable controversy over
its security

14. DES History
 IBM developed Lucifer cipher
 by team led by Feistel in late 60’s
 used 64-bit data blocks with 128-bit key
 then redeveloped as a commercial cipher
with input from NSA and others
 in 1973 NBS issued request for proposals
for a national cipher standard
 IBM submitted their revised Lucifer which
was eventually accepted as the DES

15. DES Design Controversy
 although DES standard is public
 was considerable controversy over design
 in choice of 56-bit key (vs Lucifer 128-bit)
 and because design criteria were classified
 subsequent events and public analysis
show in fact design was appropriate
 use of DES has flourished
 especially in financial applications
 still standardised for legacy application use

16. DES Encryption Overview

17. Initial Permutation IP
 first step of the data computation
 IP reorders the input data bits
 even bits to LH half, odd bits to RH half
 quite regular in structure (easy in h/w)
 example:
IP(675a6967 5e5a6b5a) = (ffb2194d
004df6fb)

18. DES Round Structure
 uses two 32-bit L & R halves
 as for any Feistel cipher can describe as:
Li = Ri–1
Ri = Li–1  F(Ri–1, Ki)
 F takes 32-bit R half and 48-bit subkey:
 expands R to 48-bits using perm E
 adds to subkey using XOR
 passes through 8 S-boxes to get 32-bit result
 finally permutes using 32-bit perm P

19. DES Round Structure

20. Substitution Boxes S
 have eight S-boxes which map 6 to 4 bits
 each S-box is actually 4 little 4 bit boxes
 outer bits 1 & 6 (row bits) select one row of 4
 inner bits 2-5 (col bits) are substituted
 result is 8 lots of 4 bits, or 32 bits
 row selection depends on both data & key
 feature known as autoclaving (autokeying)
 example:
 S(18 09 12 3d 11 17 38 39) = 5fd25e03

21. DES Key Schedule
 forms subkeys used in each round
 initial permutation of the key (PC1) which
selects 56-bits in two 28-bit halves
 16 stages consisting of:
• rotating each half separately either 1 or 2 places
depending on the key rotation schedule K
• selecting 24-bits from each half & permuting them
by PC2 for use in round function F
 note practical use issues in h/w vs s/w

22. DES Decryption
 decrypt must unwind steps of data computation
 with Feistel design, do encryption steps again
using subkeys in reverse order (SK16 … SK1)
 IP undoes final FP step of encryption
 1st round with SK16 undoes 16th encrypt round
 ….
 16th round with SK1 undoes 1st encrypt round
 then final FP undoes initial encryption IP
 thus recovering original data value

23. Avalanche Effect
 key desirable property of encryption alg
 where a change of one input or key bit
results in changing approx half output bits
 making attempts to “home-in” by guessing
keys impossible
 DES exhibits strong avalanche

24. Strength of DES – Key Size
 56-bit keys have 256 = 7.2 x 1016 values
 brute force search looks hard
 recent advances have shown is possible
 in 1997 on Internet in a few months
 in 1998 on dedicated h/w (EFF) in a few days
 in 1999 above combined in 22hrs!
 still must be able to recognize plaintext
 must now consider alternatives to DES

25. Strength of DES – Analytic
Attacks
 now have several analytic attacks on DES
 these utilise some deep structure of the cipher
 by gathering information about encryptions
 can eventually recover some/all of the sub-key bits
 if necessary then exhaustively search for the rest
 generally these are statistical attacks
 include
 differential cryptanalysis
 linear cryptanalysis
 related key attacks

26. Strength of DES – Timing
Attacks
 attacks actual implementation of cipher
 use knowledge of consequences of
implementation to derive information about
some/all subkey bits
 specifically use fact that calculations can
take varying times depending on the value
of the inputs to it
 particularly problematic on smartcards

27. Differential Cryptanalysis
 one of the most significant recent (public)
advances in cryptanalysis
 known by NSA in 70's cf DES design
 Murphy, Biham & Shamir published in 90’s
 powerful method to analyse block ciphers
 used to analyse most current block ciphers
with varying degrees of success
 DES reasonably resistant to it, cf Lucifer

28. Differential Cryptanalysis
 a statistical attack against Feistel ciphers
 uses cipher structure not previously used
 design of S-P networks has output of
function f influenced by both input & key
 hence cannot trace values back through
cipher without knowing value of the key
 differential cryptanalysis compares two
related pairs of encryptions

29. Differential Cryptanalysis
Compares Pairs of Encryptions
 with a known difference in the input
 searching for a known difference in output
 when same subkeys are used

30. Differential Cryptanalysis
 have some input difference giving some
output difference with probability p
 if find instances of some higher probability
input / output difference pairs occurring
 can infer subkey that was used in round
 then must iterate process over many
rounds (with decreasing probabilities)

31. Differential Cryptanalysis

32. Differential Cryptanalysis
 perform attack by repeatedly encrypting plaintext pairs
with known input XOR until obtain desired output XOR
 when found
 if intermediate rounds match required XOR have a right pair
 if not then have a wrong pair, relative ratio is S/N for attack
 can then deduce keys values for the rounds
 right pairs suggest same key bits
 wrong pairs give random values
 for large numbers of rounds, probability is so low that
more pairs are required than exist with 64-bit inputs
 Biham and Shamir have shown how a 13-round iterated
characteristic can break the full 16-round DES

33. Linear Cryptanalysis
 another recent development
 also a statistical method
 must be iterated over rounds, with
decreasing probabilities
 developed by Matsui et al in early 90's
 based on finding linear approximations
 can attack DES with 243 known plaintexts,
easier but still in practise infeasible

34. Linear Cryptanalysis
 find linear approximations with prob p != ½
P[i1,i2,...,ia]  C[j1,j2,...,jb] =
K[k1,k2,...,kc]
where ia,jb,kc are bit locations in P,C,K
 gives linear equation for key bits
 get one key bit using max likelihood alg
 using a large number of trial encryptions
 effectiveness given by: |p–1/2|

35. DES Design Criteria
 as reported by Coppersmith in [COPP94]
 7 criteria for S-boxes provide for
 non-linearity
 resistance to differential cryptanalysis
 good confusion
 3 criteria for permutation P provide for
 increased diffusion

36. Block Cipher Design
 basic principles still like Feistel’s in 1970’s
 number of rounds
 more is better, exhaustive search best attack
 function f:
 provides “confusion”, is nonlinear, avalanche
 have issues of how S-boxes are selected
 key schedule
 complex subkey creation, key avalanche

37. Summary
 have considered:
 block vs stream ciphers
 Feistel cipher design & structure
 DES
• details
• strength
 Differential & Linear Cryptanalysis
 block cipher design principles