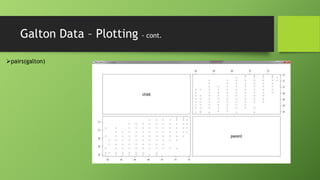
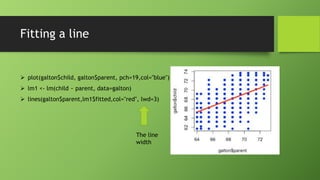
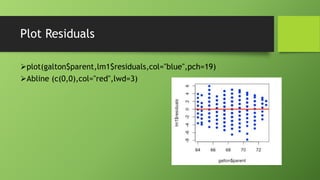
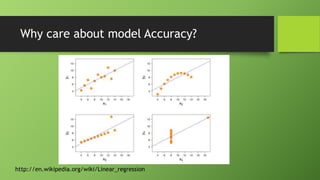
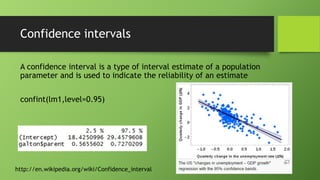
The document discusses data mining using R with a focus on regression models, demonstrating how to analyze and visualize relationships between variables using the Galton dataset. It explains the importance of model accuracy through measures such as p-values and confidence intervals, and introduces multivariate linear regression with examples. Additionally, it covers fitting models with factor variables and provides various data sources for practical applications.

1. Data Mining with R
Regression models
Hamideh Iraj
Hamideh.iraj@ut.ac.ir

2. Slides Reference
This a curation from:
Data Analysis Course
Weeks 4-5-6
https://www.coursera.org/course/dataanalysis

3. Galton Data – Introduction
library(UsingR)
data(galton)
---------------------------------Head(galton)
Tail(galton)
---------------------------------Dim(galton)
Str(galton)
summary(galton)
summary(galton$child)

4. Galton Data - Plotting
par(mfrow=c(1,2))
hist(galton$child,col="blue",breaks=100)
hist(galton$parent,col="blue",breaks=100)

5. Galton Data – Plotting
pairs(galton)
- cont.

6. What is Regression Analysis?
regression analysis is a statistical process for estimating the
relationships among variables. It includes many techniques for
modeling and analyzing several variables, when the focus is on the
relationship between a dependent variable and one or
more independent variables.
http://en.wikipedia.org/wiki/Regression_analysis

7. Fitting a line
 plot(galton$child, galton$parent, pch=19,col="blue")
 lm1 <- lm(child ~ parent, data=galton)
 lines(galton$parent,lm1$fitted,col="red", lwd=3)
The line
width

8. Plot Residuals
plot(galton$parent,lm1$residuals,col="blue",pch=19)
Abline (c(0,0),col="red",lwd=3)

9. Linear Model Coefficients
>Summary(lm1)
lm1$coeff

10. Why care about model Accuracy?
http://en.wikipedia.org/wiki/Linear_regression

11. Model Accuracy Measures
P-value
Confidence Interval
R2
Adjusted R2

12. P-value
Most Common Measure of Statistical Significance
Idea: Suppose nothing is going on - how unusual is it to see the estimate we got?
Some typical values (single test)
 P < 0.05 (significant)
 P < 0.01 (strongly significant)
 P < 0.001 (very significant)

13. Confidence intervals
A confidence interval is a type of interval estimate of a population
parameter and is used to indicate the reliability of an estimate
confint(lm1,level=0.95)
http://en.wikipedia.org/wiki/Confidence_interval

14. 2
R
R2 : the proportion of response variation "explained" by the
regressors in the model.
R2= 1 :the fitted model explains all variability in
R2 = 0 indicates no 'linear' relationship (for straight line
regression, this means that the straight line model is a constant line
(slope=0, intercept=bar{y}) between the response variable and
regressors).
http://en.wikipedia.org/wiki/Coefficient_of_determination

15. Adjusted R2
The use of an adjusted R2 (often written as bar R^2 and pronounced
"R bar squared") is an attempt to take account of the phenomenon
of the R2 automatically and spuriously increasing when extra
explanatory variables are added to the model.
http://en.wikipedia.org/wiki/Coefficient_of_determination

16. Predicting with Linear Regression
coef(lm1)[1] + coef(lm1)[2]*80
newdata <- data.frame(parent=80)
predict(lm1,newdata)

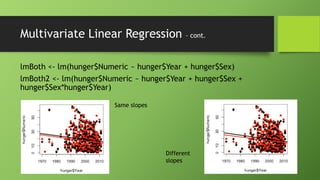
17. Multivariate Linear Regression
WHO childhood hunger data
Dataset:
http://apps.who.int/gho/athena/data/GHO/WHOSIS_000008.csv?pr
ofile=text&filter=COUNTRY:*
hunger <- read.csv("./hunger.csv")
hunger <- hunger[hunger$Sex!="Both sexes", ]

18. Multivariate Linear Regression
– cont.
lmBoth <- lm(hunger$Numeric ~ hunger$Year + hunger$Sex)
lmBoth2 <- lm(hunger$Numeric ~ hunger$Year + hunger$Sex +
hunger$Sex*hunger$Year)
Same slopes
Different
slopes

19. Model Selection
step(lmBoth2)

20. Regression with Factor Variables
 Outcome is still quantitative
 Covariate(s) are factor variables
 Fitting lines = fitting means
 Want to evaluate contribution of all factor levels at once

21. Regression with Factor Variables – cont.
 Dataset: http://www.rossmanchance.com/iscam2/data/movies03RT.txt
 movies <- read.table("./movies.txt",sep="t",header=T,quote="")
 head(movies)

22. Regression with Factor Variables – cont.
 lm2 <- lm(movies$score ~ as.factor(movies$rating))
 summary(lm2)