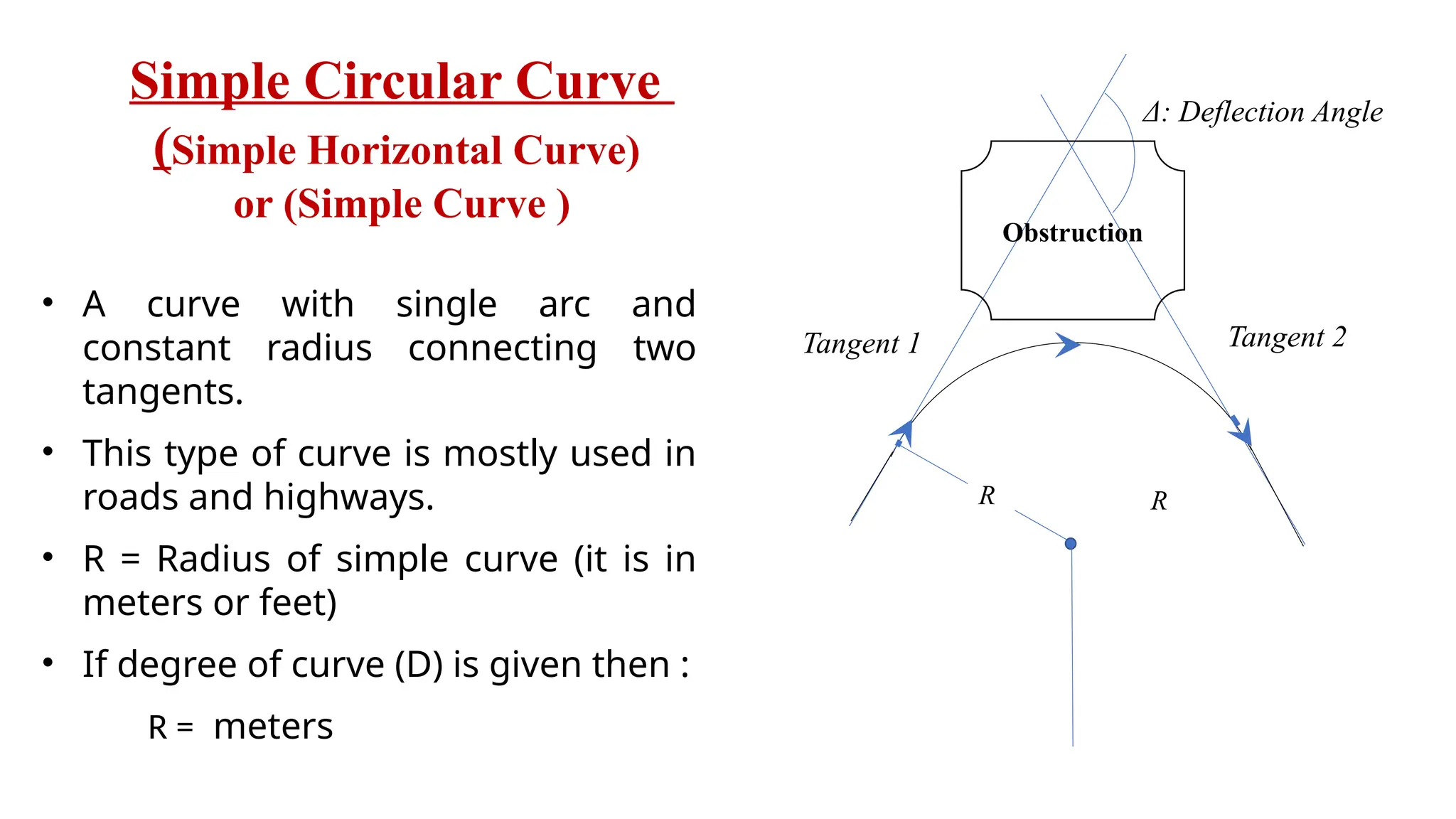
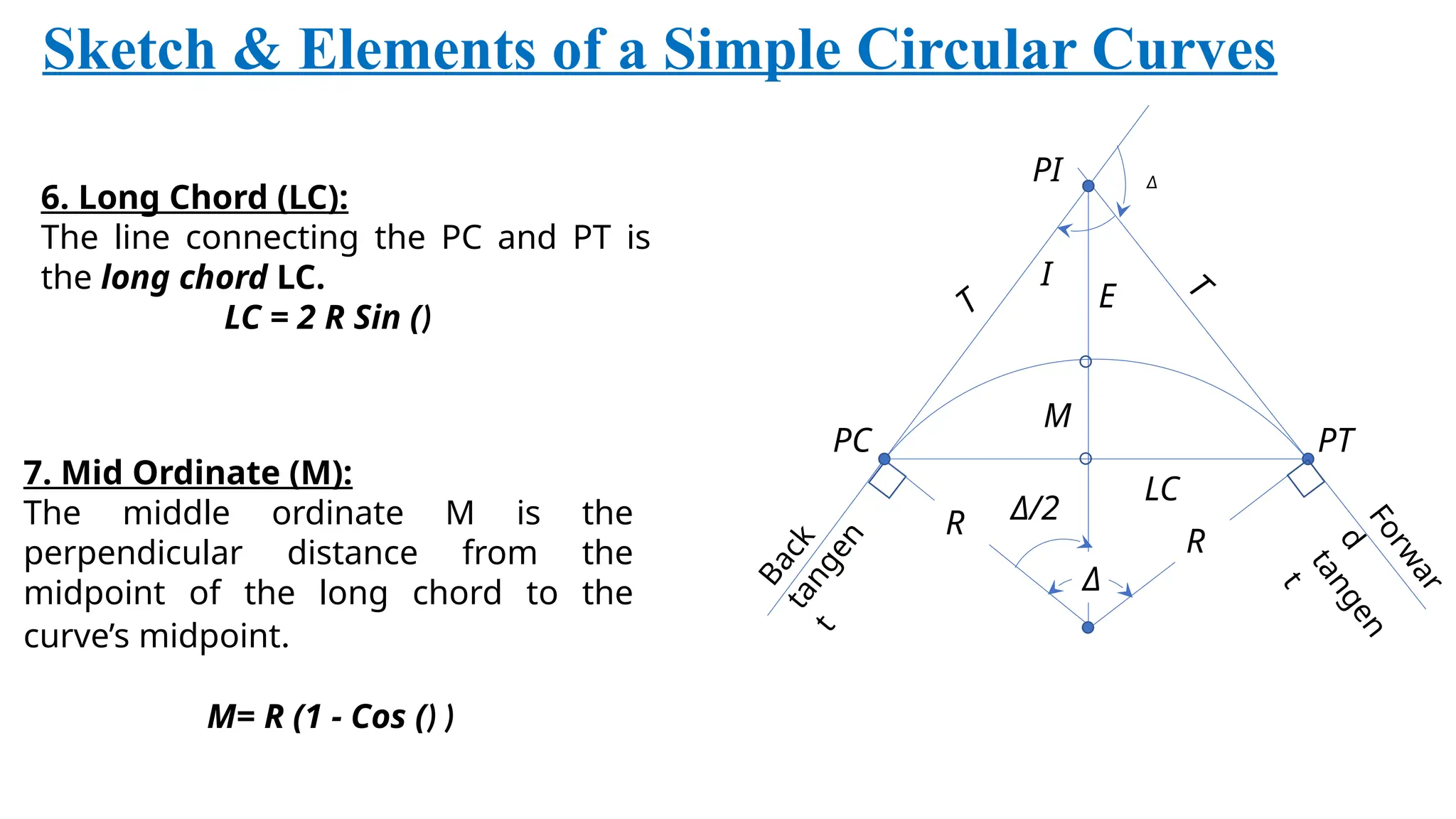
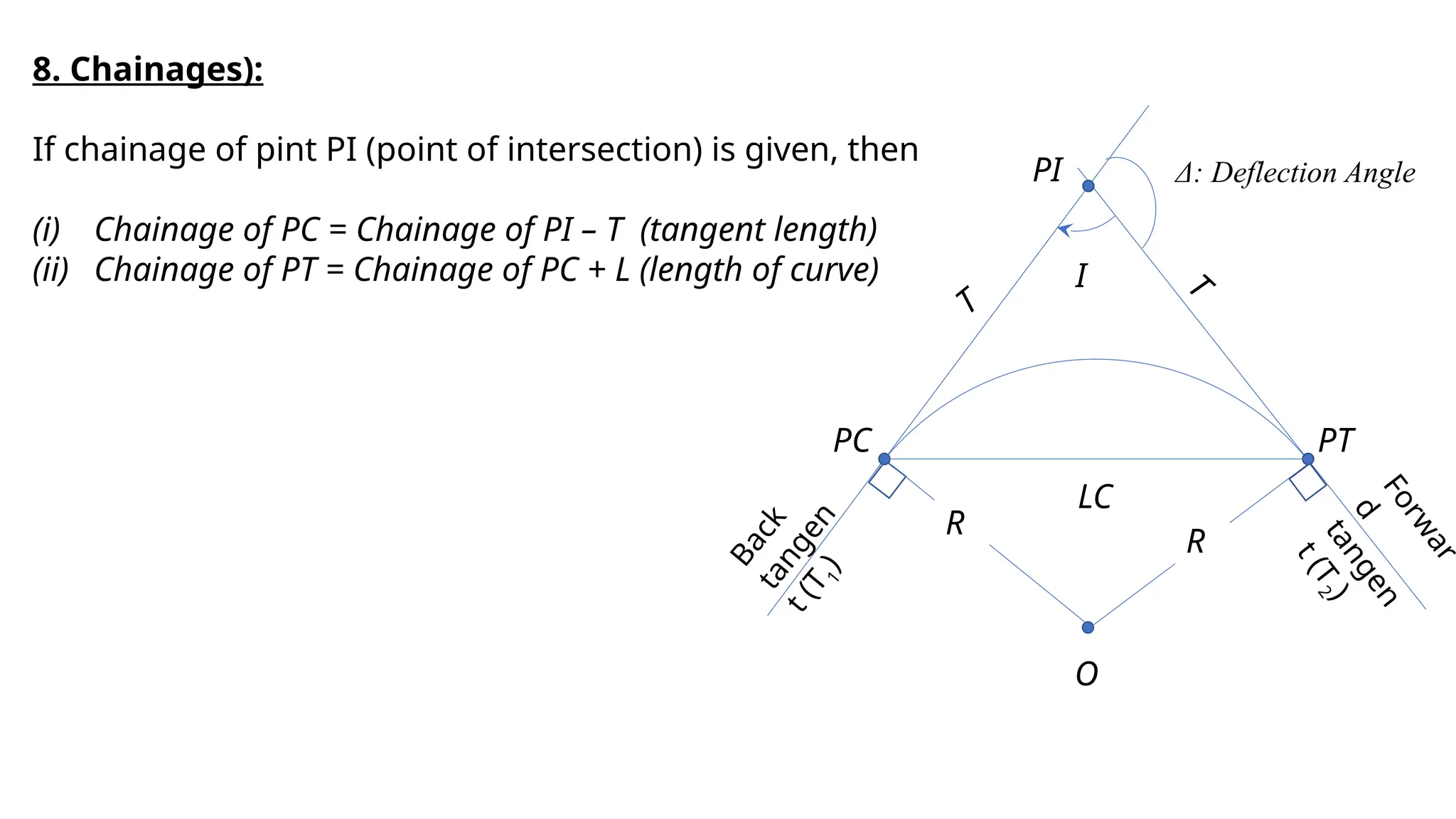
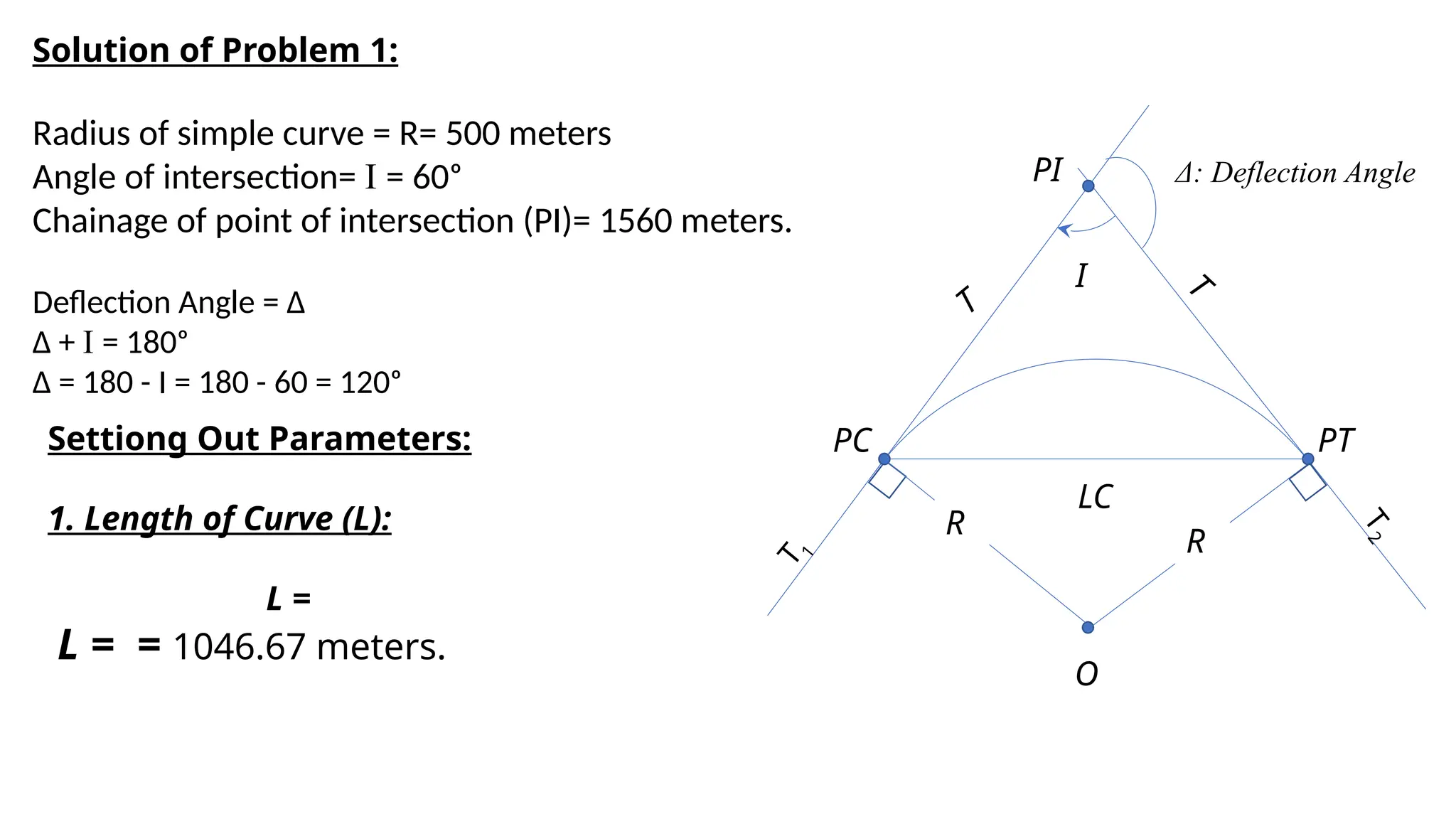
The document outlines the characteristics and calculations related to simple circular curves used in road and highway construction, including definitions of key points and parameters such as radius, deflection angle, tangent length, length of curve, long chord, and mid ordinate. It provides equations for these parameters and examples of calculations based on specified data. Additionally, it addresses problems related to curve setting out parameters and chainages for specific scenarios.

1. Simple Circular Curve
1

2. Obstruction
Tangent 1 Tangent 2
R R
Δ: Deflection Angle
Simple Circular Curve
(Simple Horizontal Curve)
or (Simple Curve )
• A curve with single arc and
constant radius connecting two
tangents.
• This type of curve is mostly used in
roads and highways.
• R = Radius of simple curve (it is in
meters or feet)
• If degree of curve (D) is given then :
R = meters

3. Sketch & Elements of a Simple Circular Curves
PC PT
PI
R
R
I
B
a
c
k
t
a
n
g
e
n
t
(
T
1
)
F
o
r
w
a
r
d
t
a
n
g
e
n
t
(
T
2
)
PI: Point of Intersection of two tangents..
3. Points:
PC: Point of curve or point of commencement
of curve; start point of the curve.
PT: Point of tangency; end point of the curve.
1. Tangents:
Back Tangents or Original Straight Line (T1)
Forward Tangents or Deflected line (T2)
T
T
LC
O
Δ: Deflection Angle
2. Deflection Angle (Δ ):
It is angle of change in direction. It is an external
angle from line T1 to T2 as shown in sketch.
Δ + I = 180
Where I = Angle of Intersection

4. Sketch & Elements of a Simple Circular Curves
PC PT
PI
R
R
I
B
a
c
k
t
a
n
g
e
n
t
(
T
1
)
F
o
r
w
a
r
d
t
a
n
g
e
n
t
(
T
2
)
T
T
5. Tangent length (T):
The distance from point PC to PI
(or PI to PT ) is called the tangent length, T.
Distance from PC to PI and PI and PT are
equal.
T = R tan ()
LC
O
Δ: Deflection Angle
4. Length of Curve (L):
It the curved length from point PC to PT. It
the length (arc length) of simple circular
curve.
L =
R is in meters or feet
Δ = Deflection angle in degrees.

5. PC PT
PI
R
R
Δ
I
M
E
Δ
B
a
c
k
t
a
n
g
e
n
t
F
o
r
w
a
r
d
t
a
n
g
e
n
t
Δ/2
T
T
LC
Sketch & Elements of a Simple Circular Curves
6. Long Chord (LC):
The line connecting the PC and PT is
the long chord LC.
LC = 2 R Sin ()
7. Mid Ordinate (M):
The middle ordinate M is the
perpendicular distance from the
midpoint of the long chord to the
curve’s midpoint.
M= R (1 - Cos () )

6. PC PT
PI
R
R
I
B
a
c
k
t
a
n
g
e
n
t
(
T
1
)
F
o
r
w
a
r
d
t
a
n
g
e
n
t
(
T
2
)
T
T
LC
O
Δ: Deflection Angle
8. Chainages):
If chainage of pint PI (point of intersection) is given, then
(i) Chainage of PC = Chainage of PI – T (tangent length)
(ii) Chainage of PT = Chainage of PC + L (length of curve)

7. 7
• Problem No: 1
Compute all the setting out Parameters (length of curve, tangent
length, long chord and mid ordinate) of a simple circular curve and
Chainages at start and end point of curve with the help of following
data.
Radius of simple curve = 500 meters
Angle of intersection= 60ᵒ
Chainage of point of intersection (PI)= 1560 meters.

8. 8
• Problem No: 1
Compute all the setting out Parameters (length of curve, tangent
length, long chord and mid ordinate) of a simple circular curve and
Chainages at start and end point of curve with the help of following
data.
Radius of simple curve = 500 meters
Angle of intersection= 60ᵒ
Chainage of point of intersection (PI)= 1560 meters.

9. PC PT
PI
R
R
I
T
1
T
2
T
T
LC
O
Δ: Deflection Angle
Solution of Problem 1:
Radius of simple curve = R= 500 meters
Angle of intersection= I = 60ᵒ
Chainage of point of intersection (PI)= 1560 meters.
Deflection Angle = Δ
Δ + I = 180ᵒ
Δ = 180 - I = 180 - 60 = 120ᵒ
Settiong Out Parameters:
1. Length of Curve (L):
L =
L = = 1046.67 meters.

10. 10
2. . Tangent length (T):
T = R tan () = 500 x tan (120/2) = 866.02 meters
3. Long Chord (LC):
LC = 2 R Sin ()
LC = 2x500x Sin () = 866.02 meters
4. Mid Ordinate (M):
M= R (1 - Cos () ) = 500 (1 - Cos () ) = 250 meters.
5. Chainages:
(i) Chainage of PC = Chainage of PI – T (tangent length) = 1560-866.02= 693.98 meters
(ii) Chainage of PT = Chainage of PC + L (length of curve) = 693.98 + 1046.67 = 1740.65
meters.

11. 11
• Problem No: 2
Draw the sketch and calculate all the setting out Parameters and
Chainages at start and end point of a simple horizontal curve of a
railway track with the help of following data.
Degree of simple curve = 5ᵒ curve
Angle of intersection= 100ᵒ
Chainage of point of intersection (PI)= 1610 meters.

12. Problem No: 3
In a simple circular curve, an angle of deflection is 28°24’, the station
of the PI is 6+340 meters, and terrain conditions require the minimum
radius permitted by the specifications is 286 meters. Calculate the PC
and PT stationing and the external and middle ordinate distances for
this curve.