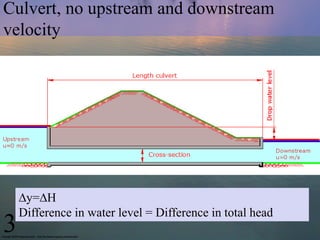
This document discusses fluid dynamics concepts related to flow in pipes and closed conduits including turbulent flow, local head losses, and partially full pipes. It then provides equations and explanations for calculating head losses and discharge in culverts under various conditions: with and without upstream/downstream velocities, for submerged culverts, and examples of calculating discharge given water level changes and culvert dimensions. Formulas are given for inlet, friction, and outlet losses as well as calculating total head loss, discharge coefficients, and drawing head and water level lines.

1. CU06997 Fluid Dynamics
Flow in pipes and closed conduits
4.5 Turbulent flow (page 100-111)
4.6 Local head losses (page 112-116)
4.7 Partially full pipes (page 116-121)
1

2. Culvert, no upstream and downstream
velocity
1

3. Culvert, with upstream and downstream
velocity
1

4. Culvert, no upstream and downstream
velocity 2 2
u1 u2
y1  z1   y 2  z2   H12
2g 2g
P1 P2
2
u
2 ΔΗ culvert  ξ culvert  culvert
[m]
2g

5. Friction loss, Darcy Weisbach
L
f   
4R
2

6. Inlet and outlet loss [intree en uitree verlies]
o  1
2
1 
 i    1
 
 
µ=contraction coëfficiënt (bv 0,6) [1]
2

7. Outlet los
u  0,3 u  0,5
2

8. Loss at a (open) valve [klep]
  Between 0,1 and 0,2
Loss at a non-return valve
[terugslag klep]
  approximately 1
2

9. Head (energy) loss strategy
2
u
ΔΗ  ξ  [m]
2g
2 2 2
u u u
ΔΗ total  ξ1   ξ 2   ξ... 
1 2
[m] ....
2g 2g 2g
If velocity does not change
2
u
ΔΗ total  (ξ1  ξ 2  ξ..... )  [m]
2 2g

10. Head (energy) loss culvert
o  1
2
1  L
 i    1
  f   
  4R
2
u
ΔΗ culvert  (ξ i  ξ f  ξ o )  culvert
[m]
2 2g

11. Submerged Culvert 1 [Volledig gevuld]
u2 tot  (ξ i  ξ f  ξ o  ....)
ΔΗ tot  ξ tot  c
2g
∆𝐻 𝑡𝑜𝑡 = Total Head Loss Culvert [m] 1 
2
𝜉 𝑡𝑜𝑡 = Sum of Loss coefficients [1]  i    1
 
𝑢𝑐 = Mean Fluid Velocity Culvert [m/s]  
𝜉𝑖 = Loss coefficient due to contraction [1]
l
𝜉𝑤 = Loss coefficient due to friction [1] f   
4R
𝜉𝑜 = Loss coefficient due to outlet [1]
𝜇 = Contraction coefficient [1]
𝑔 = earths gravity [m/s2] o  1
𝜆 = Friction coefficient [1]
R = Hydraulic Radius [m]
𝑙 = Length between the Head Loss [m] 2

12. Submerged Culvert 2
2
u
ΔΗ tot  ξ tot  c
2g 𝑄= 𝑢∙ 𝐴
1
m
 tot
q  m  Ac  2 g  H tot
2b

13. Submerged Culvert 2
q  m  Ac  2 g  H tot
1
m
 tot
q = Flow rate Culvert [m3/s]
𝑚 = Discharge coefficient [m]
𝐴 = Wetted Area Culvert [m2]
∆𝐻 𝑡𝑜𝑡 = Total Head Loss Culvert [m]
𝜉 𝑡𝑜𝑡 = Sum of Loss coefficients [1]
𝑔 = earths gravity [m/s2]
2b

14. Culvert, no upstream and downstream
velocity
∆y=∆H
Difference in water level = Difference in total head
3

15. Culvert, with upstream and downstream
velocity
∆y≠∆H
Difference in water level ≠ Difference in total head
3

16. Culvert, with upstream and downstream
velocity
2 2
u u
y1  z1  1
 y 2  z2  2
 H12
2g 2g
P1 P2
2
u
ΔΗculvert  ξ culvert  culvert
[m]
3 2g

17. Exercise 1 culvert
•Difference in waterlevel 1 m
•Dimensions culvert 2 x 2 m
•μ=0,6 and λ = 0,022
•Calculate Q and draw the H and y line

18. Discharge culvert

19. Exercise 2 culvert
•Difference in waterlevel 1 m
•Dimensions culvert 2 x 2 m
•μ=0,6 and λ = 0,022
•u upstream = 0,5 m/s, u downstream = 0,2 m/s
•Calculate Q and draw the H and y line