Uploaded byKai Koenig
Cryptography for developers
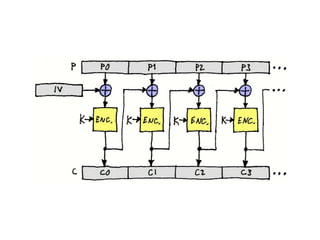
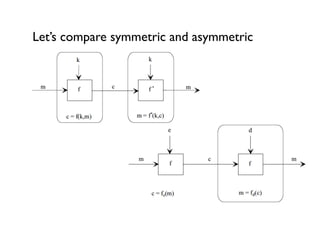
Cryptography for Developers provides an overview of cryptography concepts for developers. It defines cryptography as the encryption of plaintext into ciphertext and back again. It discusses symmetric and asymmetric cryptography, including examples like the Caesar cipher. It covers hashing of passwords for storage and discusses popular algorithms like MD5 and SHA-2. The document also summarizes public key cryptography techniques like RSA and references materials for further learning.
More Related Content
Similar to Cryptography for developers
Cryptography for developers
- 1. Cryptography for Developers Kai Koenig @AgentK
- 2. Agenda What is Cryptography? Definitions Symmetricand Asymmetric cryptography Hashing Some examples References
- 3. You might knowme from... Being active in the CF/web dev community in AU and NZ Having a very strong opinion on SOAP-based web services Having been at many webDUs in the last few years
- 4. What you mightnot know... I’m also a fully trained mathematician THERE IS A NEED FOR DEVELOPER EDUCATION ON CRYPTOGRAPHY
- 5. What is Cryptography? (and what is it good for)
- 6. Essentially Encryption of plaintextto ciphertext Decryption of ciphertext to plaintext
- 7. Essentially Encryption of plaintextto ciphertext Decryption of ciphertext to plaintext “Secrets”
- 12. Confidentiality (“Don’tworry, no one can hear us here”)
- 13. Authentication (“Who are you?”)
- 14. Integrity (“I really workfor the FBI, trust me!”)
- 15. Anonymity (“Surely no onecan trace this movie download via Torrent”)
- 16. Definition of acrypto system (I) Crypto system S = <M,C,K,E,D> M - set of plaintexts (messages) C - set of ciphertexts (encrypted messages) K - set keys E - set of encryption transforms Ek: M -> C D - set of decryption transforms Dk: C ->M
- 17. Definition of acrypto system (II) Every m∊M can be decrypted again after being encrypted (∀m∊M: Dk(Ek(m))=m) Different m∊M can not be encrypted to the same c∊C (∀k∊K,c∊C ∃! m∊M: Ek(m)=c)
- 18. Desired properties ofa crypto system Both E, D must be efficient and easy to use. Both E, D should be assumed known. It should be infeasible to deduce (without knowing k): m from c Dk from c (even if m is known) Ek from m (even if c is known) c, unless Ek and m are known
- 19. Practical application Ifyour crypto system doesn’t fulfill the desired properties, it’s most likely not secure. Common attack vectors: Ciphertext-only Known plaintext Chosen plaintext Chosen ciphertext
- 20.
- 21. DISCO Don’t Invent Super-Cryptoof your Own
- 22. Common setup Sender -Alice Receiver - Bob Adversary - “Evil person who wants to steal the message”
- 23. Private-key (symmetric) Cryptography Caesar cipher plaintext ABCDEFGHIJKLMNOPQRSTUVWXYZ ciphertext EFGHIJKLMNOPQRSTUVWXYZABCD WEBDU → AIFHY
- 24. Implementation of Caesarcipher Very easy to implement via modulo operation: For an integer m and a positive integer n, m mod n is the smallest non-negative integer r so that m=nq+r for some integer q. Caesar cipher is essentially a transformation from position n to position (n+s) mod 26.
- 25. Problems Easy tocrack with dictionary attacks (frequency of characters) Rotation cipher is too simple, make algorithm more complex? Mix alphabet? Or even more complex: Good?
- 27. Problems Symmetric cryptography(any scheme that uses a codebook or private key) suffers from a few drawbacks: Adversary learns what the code is → decoding becomes trivial If the coding scheme is used often enough over time & adversary has enough time and computing power they could break the code
- 29. Plaintext: renaissance Ciphertext: seadjsfdocr Decodethe following ciphertext: hobgxenwiee
- 30. Polyalphabetical ciphers -try it yourself Plaintext: renaissance Ciphertext: seadjsfdocr Decode the following ciphertext: hobgxenwiee
- 31. What’s considered goodand secure? Block ciphers: a block of data is encrypted at a time, using the same key on each block. Block ciphers have various modes: ECB, CBC, CFB, OFB etc... Stream ciphers: operate on a single bit at a time and provide a feedback mechanism to change the key
- 33. What’s considered goodand secure? DES (Data Encryption Standard) - considered to be insecure, mainly due to 56-bit keysize TripleDES (key bundle of 3 56-bit keys) - practically secure-ish with known theoretical attack vectors & slow!!!! AES (128-,192-,256-bit keys) - considered mostly secure, there are some related-key attack vectors (All block ciphers)
- 34. What’s considered goodand secure? Blowfish (variable key length) - there are some limited (# of rounds) attack vectors, but there’s currently no known cryptanalytic weakness Blowfish is also patent- and royalty-free. Others: Serpent, Twofish, RC6, MARS etc
- 35. Public-key (asymmetric) Cryptography Protocol: Both Alice and Bob have a public and private key (key pair) Each participant’s public key is made public Alice encrypts a message to Bob with Bob’s public key. Bob decrypts the message with his private key: m = Sb(Pb(m))
- 36.
- 37. Let’s compare symmetricand asymmetric
- 38. The hard partof public-key cryptography Bob’s dilemma: Sb and Pb have to be easily computable for him. Also: Sb has to be extremely hard to compute for everyone else but him (even if Pb is open and well known). Creating proper public-key cryptography needs a lot of know-how in discrete mathematics.
- 39. A simple (unsecure)public-key example Messages: integers between 1 and 999 Bob’s public key is Pb(M)=rev(1000-M) Bob’s private key is Sb(C)=1000-rev(C) Alice: M=167 therefore C=rev(1000-167)=rev(833)=338 Bob: Receives C=338 therefore M=1000- rev(338)=1000-833=167
- 40. So... WHAT EXACTLYis the challenge?
- 41. Example was flawedbecause if you know Pb, you can easily figure out Sb. The challenge is to design a function Pb so that even if you know Pb and C=Pb(M) it is exceptionally difficult to figure out what M is.
- 42. A better (andmore famous PK crypto system) RSA: Rivest-Shamir-Adleman Built on the idea of “mod n” calculations in arithmetic body Zn Let’s do that!
- 44.
- 45. We don’t haveenough time to introduce: Zn and arithmetic in Zn Inverses, Greatest Common Divisors Euclid’s Division Theorem Fermat’s Little Theorem (this is the core of RSA)
- 46. How does RSAwork though? Bob’s chooses an RSA key: (1) Choose 2 large prime numbers p and q (2) n = p·q (3) Choose e ≠ 1 so that e is relatively prime to (p − 1)·(q − 1) (4) Compute d = e−1 mod (p − 1)·(q − 1) (5) Publish e and n (6) Keep d secret and keep the factorisation n = p·q secret Alice sends to Bob: (1) Alice reads the public directory for Bob’s keys e and n (2) Compute y = xe mod n (3) Send y to Bob Bob does the following: (4) Receive y from Alice (5) Compute z = yd mod n, using secret key d (6) Read z
- 48. The trick is: There’sno scheme or algorithm to calculate the e-th root mod n (and break the code). Someone who doesn’t know the prime factorisation of n = p·q can not break the code analytically. Modular exponentiation is a one-way function. Note: BRUTE FORCE is still possible!
- 49. What’s considered goodand secure? RSA (min suggested key length today is 2048- bit, rather 3072-bit) - still the most common public key crypto system and with long keys very secure Others: Diffie-Hellman, DSA, various PKCS Worth mentioning: Elliptic Curve Cryptography - field of current research
- 50. Hashing Speaking ofone-way functions...how do you store passwords? A hash function is a one-way function that can’t be reversed. You always want to store hashed passwords in your DB.
- 51. Problems with MD5hashing Even though hashing is one-way, there are MD5 hash libraries/websites Google the hash http://www.lib.muohio.edu/multifacet/record/az-4602da187c6e221d00d02826db1bfd6a MD5 is not collision resistant and considered insecure now, use SHA-2 instead!
- 53. Salting The samehash input creates the same hash output: test12→60474c9c10d7142b7508ce7a50acf414 But if you salt every password, the hash value is much harder to reverse-engineer: <userID>test12<RandomSalt>→...
- 54. References An Overviewof Cryptography http://garykessler.net/library/crypto.html CS651 (Principles of Cryptography) Lecture Notes http://www.cs.virginia.edu/~shelat/651/www/index.html CS70 (Discrete Mathematics for Computer Scientists) Lecture Notes http://www.cs.berkeley.edu/~daw/teaching/cs70-s05/ Various Cryptography and Number Theory Articles http://di-mgt.com.au/crypto.html RSA in Javascript http://www.ohdave.com/rsa/ Recommended text books with further (deeper) information: Discrete Mathematics for Computer Scientists http://www.amazon.com/Discrete-Mathematics-Computer-Scientists-Cliff/dp/0132122715/ref=pd_sim_b_1 Introduction to Modern Cryptography: Principles and Protocols http://www.amazon.com/Introduction-Cryptography-Chapman-Network-Security/dp/1584885513/
- 55. Photo credits http://www.flickr.com/photos/stevensnodgrass/4459943069 http://www.flickr.com/photos/mattkieffer/6212412212/ http://www.flickr.com/photos/-marlith-/6118342742/ http://www.flickr.com/photos/wikidave/6878554296 http://www.flickr.com/photos/thomasleuthard/5853471062 http://www.flickr.com/photos/contemplativechristian/2538196687 http://www.flickr.com/photos/klg19/5979330604 http://www.flickr.com/photos/sloshay/5382691989/ http://www.flickr.com/photos/11939863@N08/3794105536 http://www.flickr.com/photos/franganillo/3734200307 http://en.wikipedia.org/wiki/File:Enigma_rotors_with_alphabet_rings.jpg http://www.cs.rit.edu/~ark/lectures/https02/https.shtml
Editor's Notes
- #2 \n
- #3 \n
- #4 \n
- #5 \n
- #6 \n
- #7 \n
- #8 \n
- #9 \n
- #10 \n
- #11 \n
- #12 \n
- #13 \n
- #14 \n
- #15 \n
- #16 \n
- #17 \n
- #18 Ciphertext only: Attacker knows limited number of ciphertexts and wants to get the plaintexts and keys\nKP: attacker knows limited number of ciphers & their plaintexts and wants to get the key\nCP: Attacker knows encryption function (not key) and can encrypt his own plaintexts. Wants to be able to decrypt and get key\nCC: Attacker knows decryption function (not key) and can decrypt spied ciphers. Wants to get key \n
- #19 \n
- #20 \n
- #21 \n
- #22 Can be shifted by as many characters as one likes\n
- #23 \n
- #24 Pure shift cipher: Crack by brute force - just <length of alphabet keys>\nSubstitution/mix cipher: Number of keys <length of alphabet>! - for 26 it&#x2019;s > 4*10^26 -> dictionary attack\n
- #25 \n
- #26 \n
- #27 r->s 1\ne->e 0\nn->a 13\na->d 3\ni->j1\ns->s 0\ns->f 13\n\nt->s\nh->h\nc->q\nv->s\n\n
- #28 r->s 1\ne->e 0\nn->a 13\na->d 3\ni->j1\ns->s 0\ns->f 13\n\nt->s\nh->h\nc->q\nv->s\n\n
- #29 \n
- #30 \n
- #31 The first key-recovery attacks on full AES were due to Andrey Bogdanov, Dmitry Khovratovich, and Christian Rechberger, and were published in 2011.[22] The attack is based on bicliques and is faster than brute force by a factor of about four. It requires 2126.1 operations to recover an AES-128 key. For AES-192 and AES-256, 2189.7 and 2254.4 operations are needed, respectively.\n
- #32 \n
- #33 Pb public key\n\nSb secret key\n
- #34 \n
- #35 \n
- #36 Problem is that we need to find a function that&#x2019;s really hard to apply but extremely hard to reverse.\n
- #37 \n
- #38 \n
- #39 \n
- #40 \n
- #41 \n
- #42 \n
- #43 One might ask: If Bob publishes e and n and Alice encrypts a message x by y = xe mod n\nWHY THE HELL can&#x2019;t an ADVERSARY who learns xe mod n not just compute the e-th root mod n and break the code?\np = 3, q = 11. e can be: 7, 11, 13, 17, 19 (not 5)\nn=33, e=7 public key d=3 => e*d=1(mod 20) -> 7*d=1(mod20)\n\n\n\n\n
- #44 \n
- #45 impertant - distinction between brute force cracking and analytic crackign\n
- #46 PKCS: Public Key Cryptography standards\n
- #47 Very common password-storage issue\n\n
- #48 What would a password cracker do if they get access to your hash&#x2019;ed database of user accounts/passwords?\n\nLookup tables -> Rainbow Tables\n\nA collision attack exists that can find collisions within seconds on a computer with a 2.6 GHz Pentium 4 processor\n\nMD5 digests have been widely used in the software world to provide some assurance that a transferred file has arrived intact. For example, file servers often provide a pre-computed MD5 (known as Md5sum) checksum for the files, so that a user can compare the checksum of the downloaded file to it. Unix-based operating systems include MD5 sum utilities in their distribution packages, whereas Windows users use third-party applications. Android ROMs also utilize this type of checksum.\n
- #49 \n
- #50 You need to make sure if you create random salts that they are crytographically safe (system.random) or whatever is usually not.\n
- #51 \n
- #52 \n