Downloaded 14 times
![Defining secrecy (take 1)
♦ Even an adversary running for an unbounded
amount of time learns nothing about the message
from the ciphertext
♦ Perfect secrecy
♦ Formally, for all distributions over the message
space, all m, and all c:
Pr[M=m | C=c] = Pr[M=m]](https://image.slidesharecdn.com/lecture2-160712051129/75/Computer-and-Network-Security-29-2048.jpg)
Uploaded byMuhammad Yousuf Abdul Qadir
Computer and Network Security
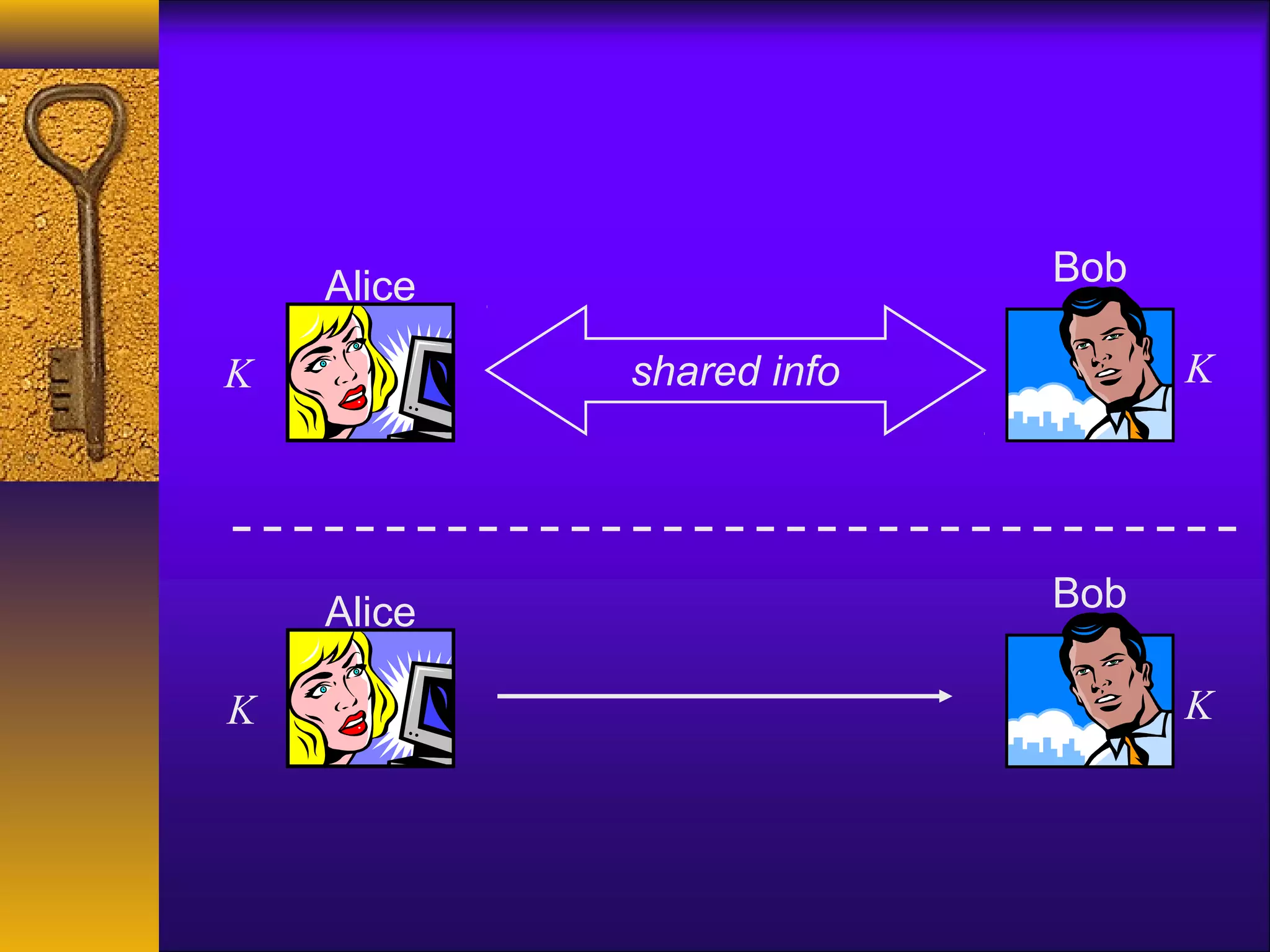
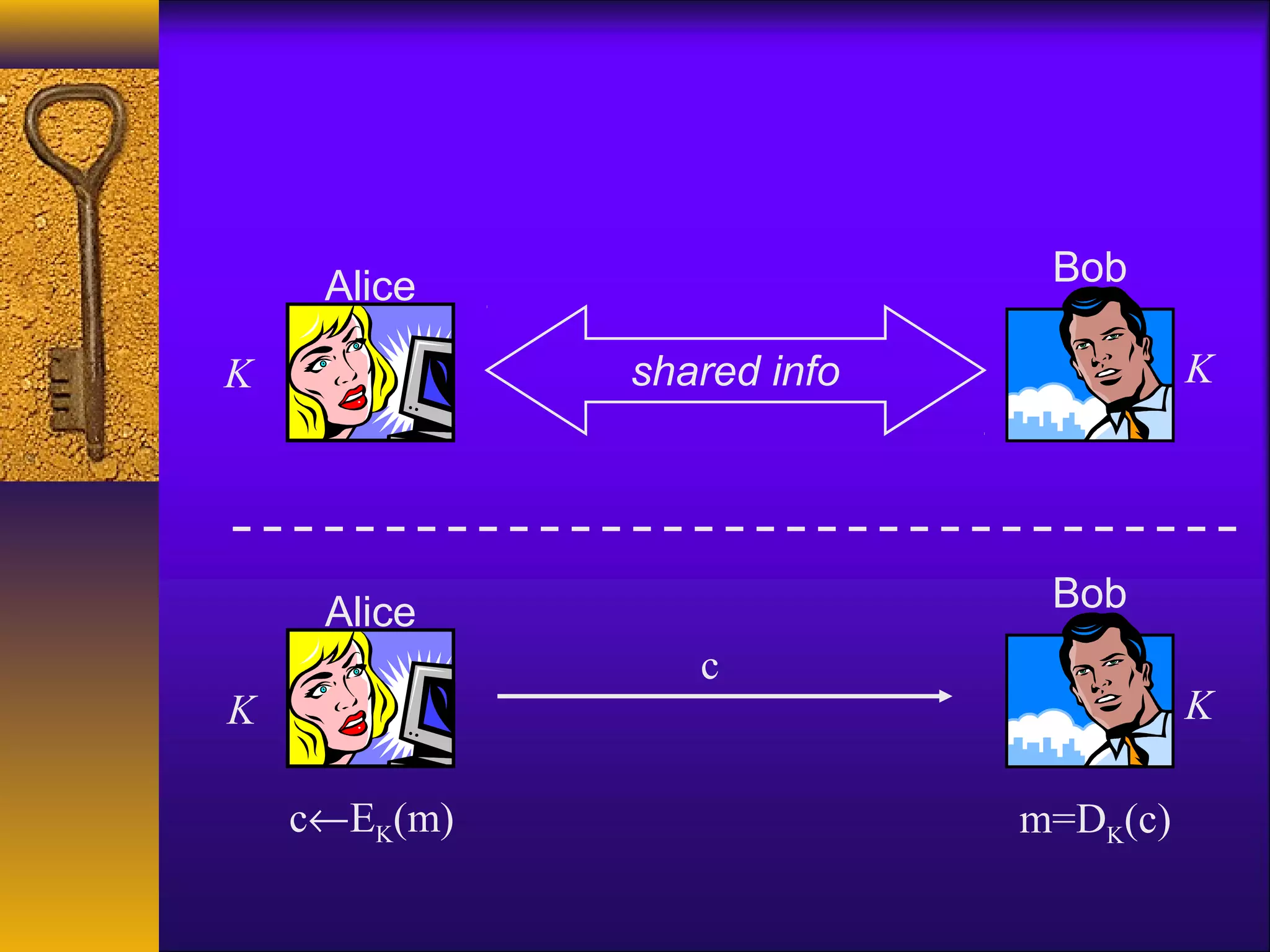
This document provides an overview of a lecture on computer and network security. It discusses an upcoming JCE tutorial and homework assignment. It also lists assigned readings and asks for comments. The rest of the document summarizes a high-level survey of cryptography, covering goals like confidentiality and integrity. It discusses private-key settings where parties share a secret key, and provides examples of simple encryption schemes like shift ciphers and their limitations. It emphasizes using standardized cryptographic algorithms.
More Related Content
Similar to Computer and Network Security
Computer and Network Security
- 1. Computer and NetworkSecurity Lecture 6
- 2. JCE tutorial ♦ Inclass next Wednesday ♦ HW1 will use it
- 3. Assigned readings fromlecture 1 ♦ “Inside the Twisted Mind of the Security Professional” ♦ “We are All Security Customers” ♦ “Information Security and Externalities” ♦ Comments?
- 4. A high-level surveyof cryptography
- 5. Caveats ♦ Everything Ipresent will be (relatively) informal – I may simplify, but I will not say anything that is an outright lie… ♦ Cryptography offers formal definitions and rigorous proofs of security (neither of which we will cover here) – For more details, take CMSC 456 in the Fall (or read my book)! ♦ If you think you already know cryptography from somewhere else (CMSC456, CISSP, your job, the news), you are probably mistaken
- 6. Goals of cryptography ♦Crypto deals primarily with three goals: – Confidentiality – Integrity (of data) – Authentication (of resources, people, systems) ♦ Other goals also considered – E.g., non-repudiation – E-cash (e.g., double spending) – General secure multi-party computation – Anonymity – …
- 7. Private- vs. public-keysettings ♦ For the basic goals, there are two settings: – Private-key / shared-key / symmetric-key / secret-key – Public-key ♦ The private-key setting is the “classical” one (thousands of years old) ♦ The public-key setting dates to the 1970s
- 8. Private-key cryptography ♦ Thecommunicating parties share some information that is random and secret – This shared information is called a key – Key is not known to an attacker – This key must be shared (somehow) in advance of their communication
- 9. To emphasize ♦ Aliceand Bob share a key K – Must be shared securely – Must be completely random – Must be kept completely secret from attacker ♦ We don’t discuss (for now) how they do this – You can imagine they meet on a dark street corner and Alice hands a USB device (with a key on it) to Bob
- 10. Private-key cryptography ♦ Forconfidentiality: – Private-key (symmetric-key) encryption ♦ For data integrity: – Message authentication codes
- 11. Canonical applications ♦ Two(or more) distinct parties communicating over an insecure network – E.g., secure communication ♦ A single party who is communicating “with itself” over time – E.g., secure storage
- 12. Alice Bob shared infoKK Alice K Bob K
- 13.
- 14. Security? ♦ We willspecify the exact threat model being addressed ♦ We will also specify the security guarantees that are ensured, within this threat model – Here: informally; CMSC 456: formally ♦ Crucial to understand these issues before crypto can be successfully deployed! – Make sure the stated threat model matches your application – Make sure the security guarantees are what you need
- 15. Security through obscurity? ♦Always assume that the full details of crypto protocols and algorithms are public – Known as Kerckhoffs’ principle – The only secret information is a key ♦ “Security through obscurity” is a bad idea… – True in general; even more true in the case of cryptography – Home-brewed solutions are BAD! – Standardized, widely-accepted solutions are GOOD!
- 16. Security through obscurity? ♦Why not? ♦ Easier to maintain secrecy of a key than an algorithm – Reverse engineering – Social engineering – Insider attacks ♦ Easier to change the key than the algorithm ♦ In general setting, much easier to share an algorithm than for everyone to use their own
- 17.
- 18. Functional definition ♦ Encryptionalgorithm: – Takes a key and a message (plaintext), and outputs a ciphertext – c ← EK(m) possibly randomized! ♦ Decryption algorithm: – Takes a key and a ciphertext, and outputs a message (or perhaps an error) – m = DK(c) ♦ Correctness: for all K, we have DK(EK(m)) = m ♦ We have not yet said anything about security…
- 19. Alice Bob shared infoKK Alice K Bob K c c←EK(m) m=DK(c)
- 20. A classic example:shift cipher ♦ Assume the English uppercase alphabet (no lowercase, punctuation, etc.) – View letters as numbers in {0, …, 25} ♦ The key is a random letter of the alphabet ♦ Encryption done by addition modulo 26 ♦ Is this secure? – Exhaustive key search – Automated determination of the key
- 21. Another example: substitutioncipher ♦ The key is a random permutation of the alphabet – Note: key space is huge! ♦ Encryption done in the natural way ♦ Is this secure? – Frequency analysis ♦ A large key space is necessary, but not sufficient, for security
- 22. Another example: Vigenerecipher ♦ More complicated version of shift cipher ♦ Believed to be secure for over 100 years ♦ Is it secure?
- 23. Attacking the Vigenerecipher ♦ Let pi (for i=0, …, 25) denote the frequency of letter i in English-language text – Known that Σ pi 2 ≈ 0.065 ♦ For each candidate period t, compute frequencies {qi} of letters in the sequence c0, ct, c2t, … ♦ For the correct value of t, we expect Σ qi 2 ≈ 0.065 – For incorrect values of t, we expect Σ qi 2 ≈ 1/26 ♦ Once we have the period, can use frequency analysis as in the case of the shift cipher
- 24. Moral of thestory? ♦ Don’t use “simple” schemes ♦ Don’t use schemes that you design yourself – Use schemes that other people have already designed and analyzed…
- 25. A fundamental problem ♦A fundamental problem with “classical” cryptography is that no definition of security was ever specified – It was not even clear what it meant for a scheme to be “secure” ♦ As a consequence, proving security was not even an option – So how can you know when something is secure? – (Or is at least based on well-studied, widely-believed assumptions)
- 26. Defining security? ♦ Whatis a good definition? ♦ Why is a good definition important?
- 27. Security goals? ♦ Adversaryunable to recover the key – Necessary, but meaningless on its own… ♦ Adversary unable to recover entire plaintext – Good, but is it enough? ♦ Adversary unable to determine any information at all about the plaintext – Formalize? – Sounds great! – Can we achieve it?
- 28. Note ♦ Even givenour definition, we need to consider the threat model – Multiple messages or a single message? – Passive/active adversary? – Chosen-plaintext attacks? ♦ The threat model matters! – The classical ciphers we have seen are immediately broken by a known-plaintext attack
- 29. Defining secrecy (take1) ♦ Even an adversary running for an unbounded amount of time learns nothing about the message from the ciphertext ♦ Perfect secrecy ♦ Formally, for all distributions over the message space, all m, and all c: Pr[M=m | C=c] = Pr[M=m]
- 30. Next time: theone-time pad; its limitations; overcoming these limitations