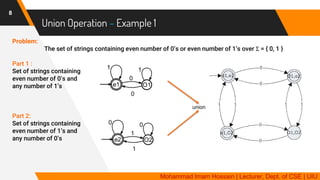
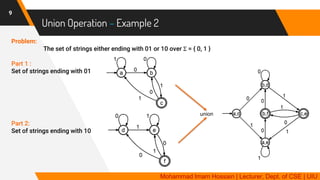
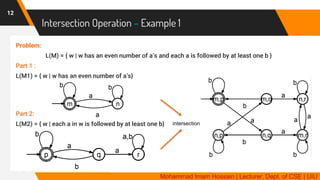
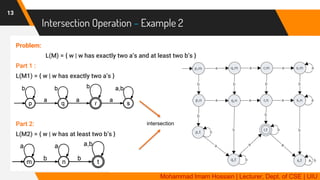
The document discusses closure properties of deterministic finite automata (DFAs), focusing on regular languages and operations including union, intersection, complement, subtraction, and reverse. It provides formal definitions and examples for each operation, illustrating how new languages can be constructed from existing ones recognized by DFAs. Additionally, it emphasizes that languages recognized by DFAs are closed under these operations, meaning that performing these operations yields new languages that can also be recognized by DFAs.