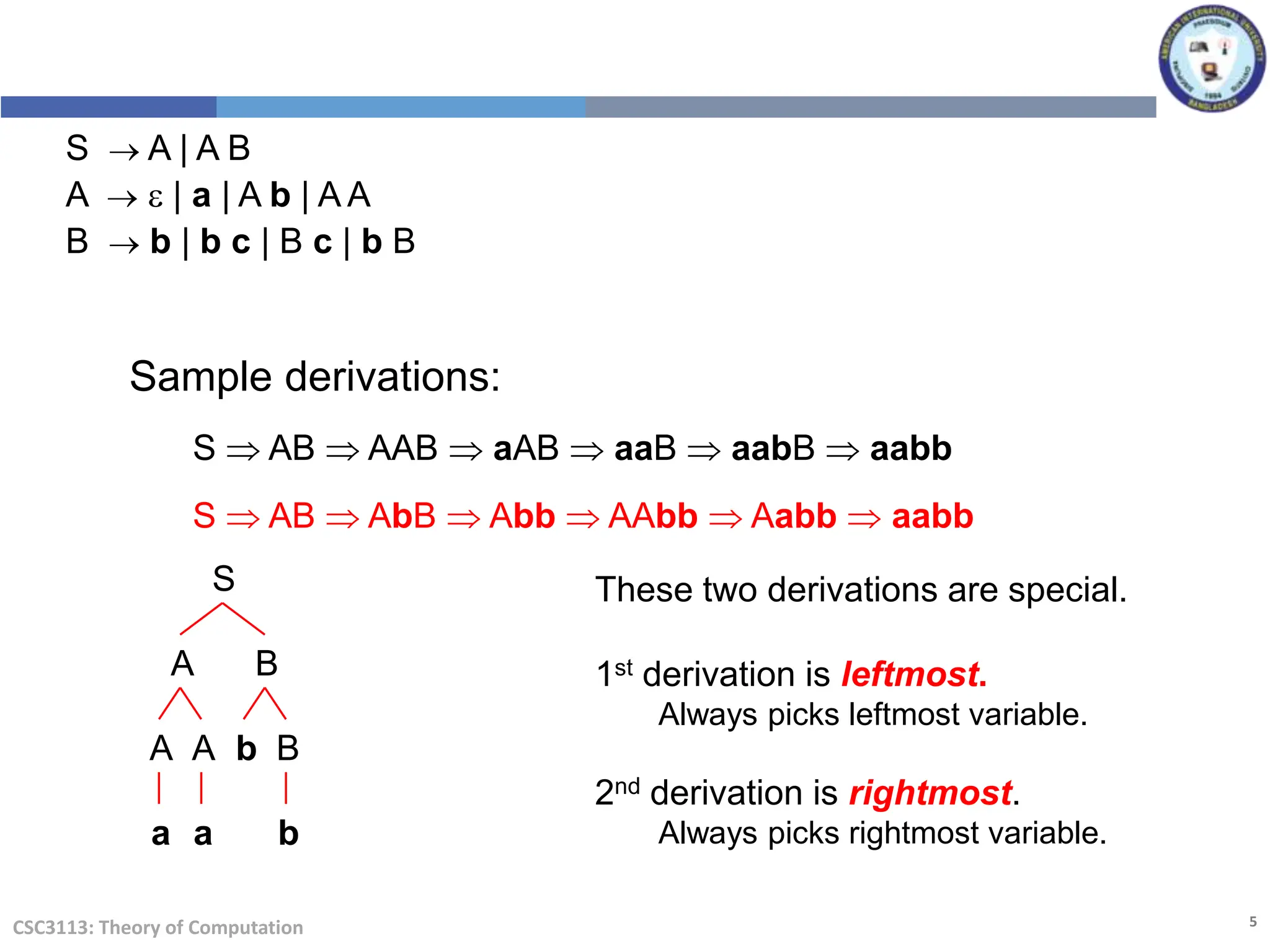
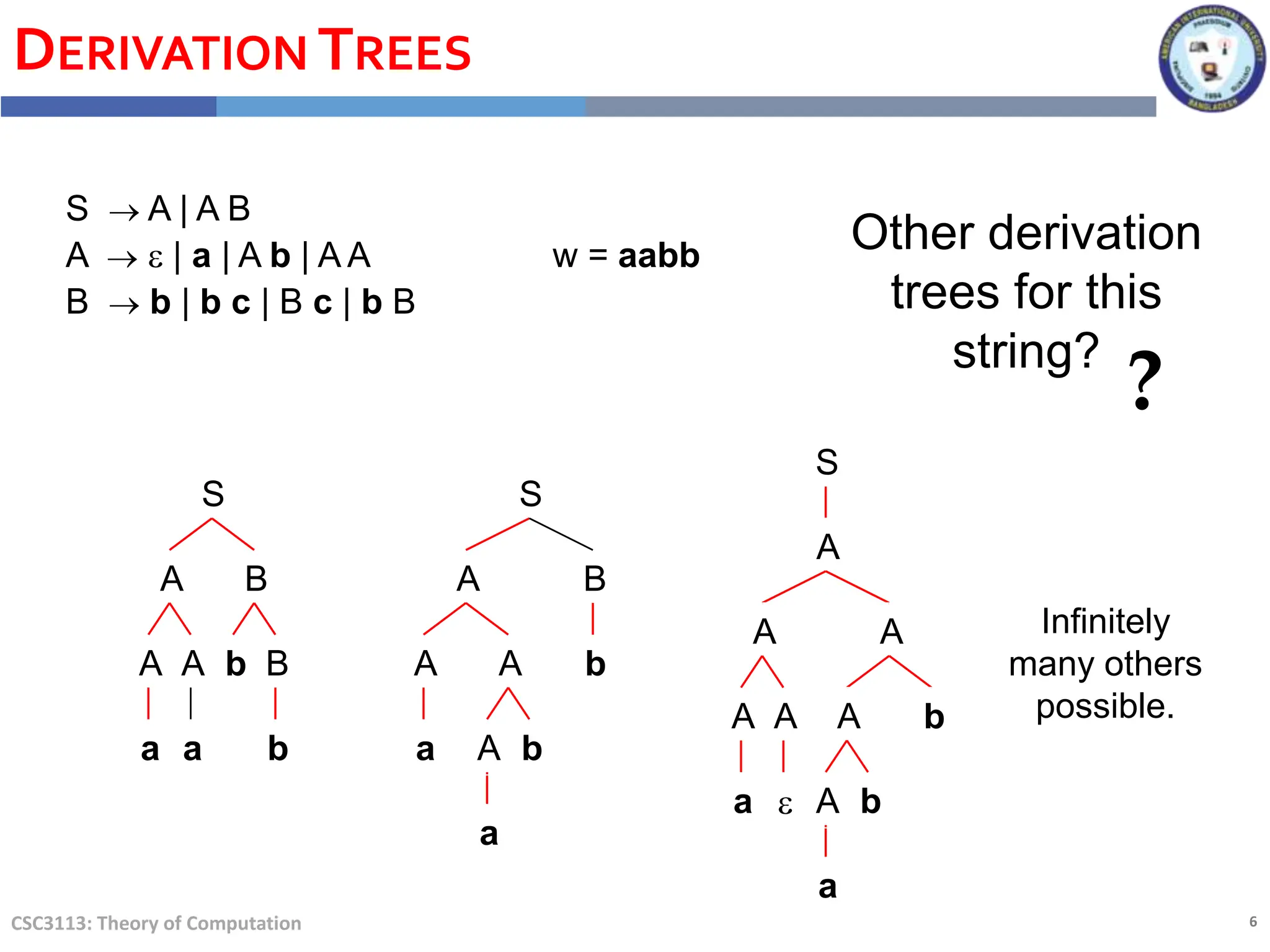
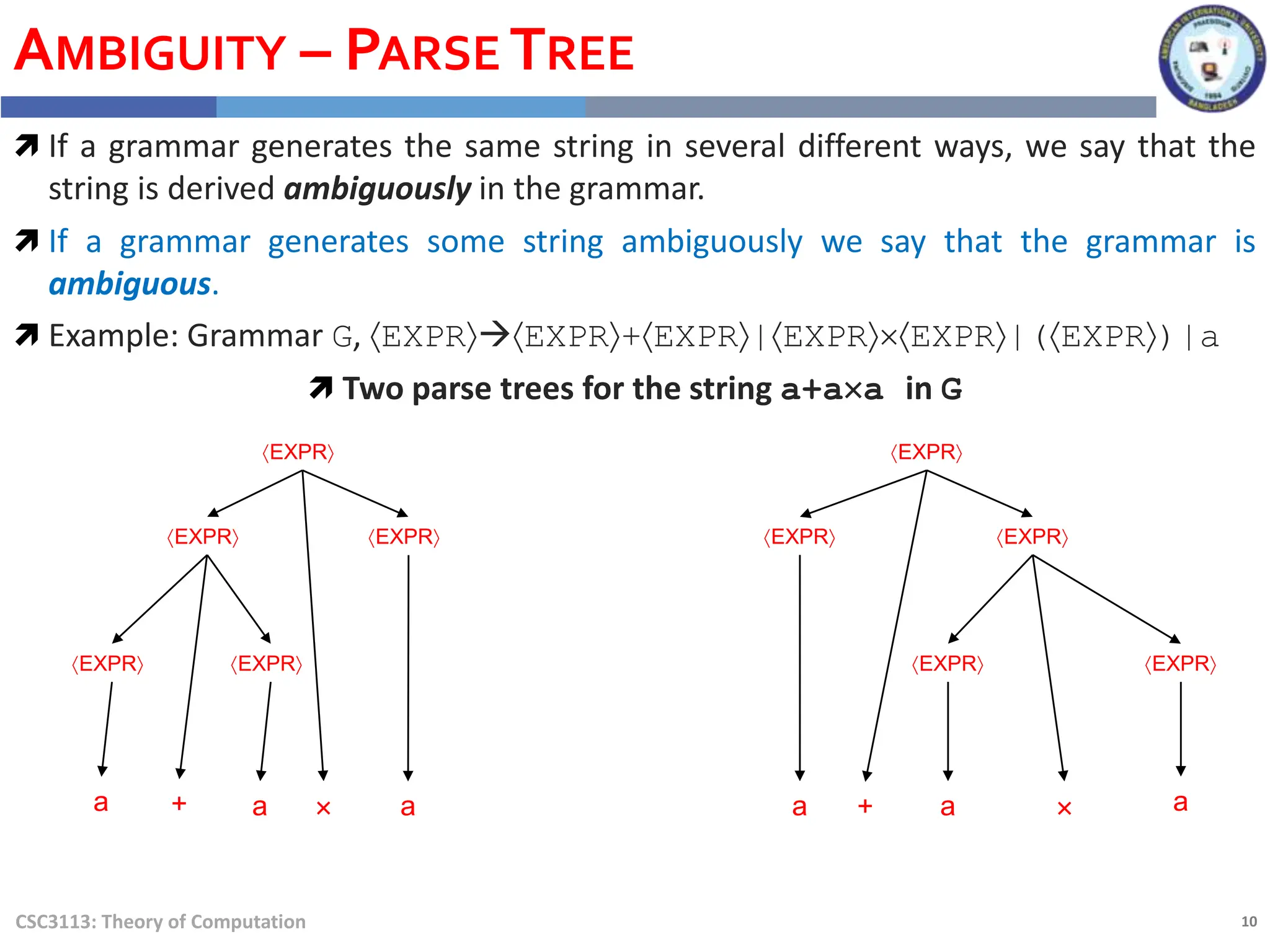
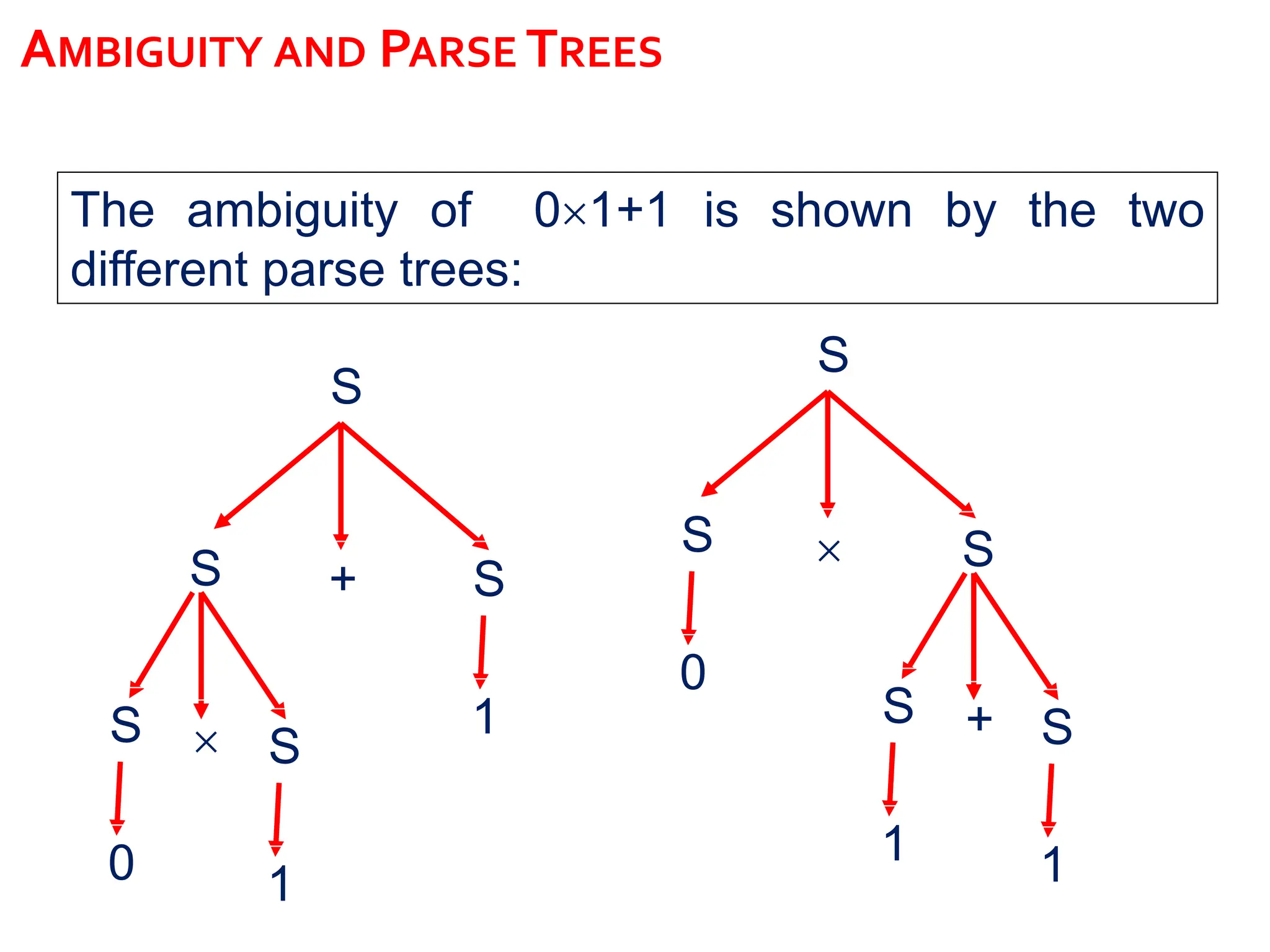
The document provides information about a lecture on context-free languages and Chomsky normal form. It includes the lecture outline, learning objectives, and learning outcomes. It discusses concepts like ambiguity, derivation trees, and converting grammars to Chomsky normal form through a series of steps like adding a new start symbol, removing epsilon rules, and eliminating unit rules. An example is provided to demonstrate the conversion process.

1. 1
Instructor:
Lecture: # Week: # Semester:
AMERICAN INTERNATIONAL UNIVERSITY-BANGLADESH
CONTEXT-FREE LANGUAGES (CFL)
CSC3113: THEORY OF COMPUTATION
10 5 Spring 2023-2024
Dr. Afroza Nahar
Department of Computer Science, Faculty of Science & Technology.
afroza@aiub.edu

2. 2
LECTURE OUTLINE
LECTURE OUTLINE
CSC3113: Theory of Computation
Ambiguity
Chomsky Normal Form (CNF)

3. 3
LEARNING OBJECTIVE
LEARNING OBJECTIVE
CSC3113: Theory of Computation
Concept and Construct of Context Free Grammar (CFG)
Concept of ambiguity and its removal from grammar.
Chomsky Normal From (CNF)

4. 4
LEARNING OUTCOME
LEARNING OUTCOME
CSC3113: Theory of Computation
ALL OUTCOME ARE REPRESENTED WITH EXAMPLES
Understand and practice the construct of CFG
Learn ambiguity in grammar and ways to identify and remove it.
Apply Chomsky Normal From (CNF) on grammar to make it
computable.

5. 5
CSC3113: Theory of Computation
Sample derivations:
S  AB  AAB  aAB  aaB  aabB  aabb
S  AB  AbB  Abb  AAbb  Aabb  aabb
S  A | A B
A  e | a | A b | A A
B  b | b c | B c | b B
S
A B
A
A B
b
a a b
These two derivations are special.
1st derivation is leftmost.
Always picks leftmost variable.
2nd derivation is rightmost.
Always picks rightmost variable.

6. 6
CSC3113: Theory of Computation
DERIVATION TREES
Infinitely
many others
possible.
S
A B
A
A b
a
a
b
A
S
A
A A
A
A b
A
a e
a
b
A
S
A B
A
A B
b
a a b
S  A | A B
A  e | a | A b | A A
B  b | b c | B c | b B
w = aabb
Other derivation
trees for this
string?
?

7. 7
CSC3113: Theory of Computation
DERIVATION TREES
 Observation: Every derivation tree corresponds to one or more derivations.
leftmost: rightmost: mixed:
S => AB S => AB S => AB
=> aAAB => Ab => Ab
=> aaAB => aAAb => aAAb
=> aaaB =>aAab => aaAb
=> aaab => aaab => aaab
 Definition: A derivation is leftmost (rightmost) if at each step in the derivation a
production is applied to the leftmost (rightmost) non-terminal in the sentential
form.
 The first derivation above is leftmost, second is rightmost, the third is neither.
Rules:
S –> AB
A –> aAA
A –> aA
A –> a
B –> bB
B –> b

8.  Example: Consider the string aaab and the preceding grammar.
S –> AB S => AB S
A –> aAA => aAAB
A –> aA => aaAB A B
A –> a => aaaB
B –> bB => aaab a A A b
B –> b
a a
S => AB S
=> aAB
=> aaAB A B
=> aaaB
=> aaab a A b
a A
a
 The string has two left-most derivations, and therefore has two distinct parse trees.

9. 9
CSC3113: Theory of Computation
EXAMPLE
Draw parse tree and leftmost derivation for the expression
ab#baab using following CFG:
S  CB
C  aCa | bCb | #B
B  AB | 
A  a | b

10. 10
CSC3113: Theory of Computation
AMBIGUITY – PARSE TREE
 If a grammar generates the same string in several different ways, we say that the
string is derived ambiguously in the grammar.
 If a grammar generates some string ambiguously we say that the grammar is
ambiguous.
 Example: Grammar G, EXPREXPR+EXPR|EXPREXPR|(EXPR)|a
 Two parse trees for the string a+aa in G
EXPR
EXPR
EXPR
EXPR
EXPR
a a
a
+ 
EXPR
EXPR
EXPR
EXPR
EXPR
a
a
a 
+

11. AMBIGUITY AND PARSE TREES
The ambiguity of 01+1 is shown by the two
different parse trees:
S
+
S
 S
1
S
0
S
1
S
 S
+ S
1
S
1
S
0

12. 12
CSC3113: Theory of Computation
AMBIGUITY - DERIVATION
When we say that a grammar generates a string ambiguously, we
mean that the string has two different parse trees, not two different
derivations.
A derivation of string w in a grammar G is a leftmost derivation if at
every step the leftmost remaining variable is the one replaced.
Then we can say, a string w is derived ambiguously in CFG G if it has
two or more different leftmost derivations.
Grammar G is ambiguous if it generates some string ambiguously.
Some CFLs can only be generated by ambiguous grammars. Such
languages are called inherently ambiguous.
Example: {0i1j2k | i=j or j=k}

13. 13
CSC3113: Theory of Computation
AMBIGUITY - DERIVATION
When we say that a grammar generates a string ambiguously, we
mean that the string has two different parse trees, not two different
derivations.
A derivation of string w in a grammar G is a leftmost derivation if at
every step the leftmost remaining variable is the one replaced.
Then we can say, a string w is derived ambiguously in CFG G if it has
two or more different leftmost derivations.
Grammar G is ambiguous if it generates some string ambiguously.
Some CFLs can only be generated by ambiguous grammars. Such
languages are called inherently ambiguous.
Example: {0i1j2k | i=j or j=k}

14. 14
CSC3113: Theory of Computation
Using Parse Tree prove that the following grammar is ambiguous for
the string 00110011.
S → 0A | 1B
A → 0AA | 1S | 1
B → 1BB | 0S | 0

15. 15
CSC3113: Theory of Computation
CHOMSKY NORMAL FORM
It is often convenient to have CFGs in simplified form. One
such form is Chomsky normal form.
A context free grammar is in Chomsky normal form if every
rule is of the form
A  BC
A  a
where a is any terminal and A, B, and C are any variables –
except that B and C may not be the start variable.
In addition S  e is permitted, where S is the start
variable.

16. 16
CSC3113: Theory of Computation
CONVERT ANY GRAMMAR GTO CHOMSKY NORMAL FORM
Add a new start symbol S0 and the new rule S0S,
where S was the original start symbol.
Eliminate all e rules of the form A  e, where A is not
the start symbol.
Add rule Ruv for every rule of the form RuAv,
where u and v are strings of variables and terminals.
Add such rules for every occurrence of A. for example,
add RuvAw, RuAvw, Ruvw for the rule of the
form RuAvAw.
Add Re for the rule of the form RA, unless we have
previously removed the rule Re.

17. 17
CSC3113: Theory of Computation
CONVERT ANY GRAMMAR GTO CHOMSKY NORMAL FORM
Eliminate all unit rules of the form A  B.
Add rule A  u for the rule of the form B  u, unless this was
a unit rule previously removed.
Here u is a string of variables and terminals.
Convert remaining rules into proper form,
RPQ and Ru.
We replace each rule of the form A  u1u2…uk with the rules
Au1A1, A1u2A2, A2u3A3, … , Ak-2uk-1uk.
Here k  3 and each ui is a variable or terminal symbol,
and Ai’s are new variables.
If k  2, replace any terminal ui in the preceding rule(s) with the
new variable Ui and the rule Uiui.
The above procedure converts a Grammar to a Chomsky
normal form. Next, we will go through an example.

18. 18
CSC3113: Theory of Computation
EXAMPLE: CONVERTING TO CNF
Original Grammar
S  ASA | aB
A  B | S
B  b | e
CNF: Rules Format
1. A variable substitute by
two variables
V1  V2V3
2. A variable substitute by
a single terminal
V1  t
3. Exception: the start
variable may have an
epsilon rule
S0  e
Conversion Steps:
1. Add a new start variable (substitute by old start variable).
2. Remove all epsilon rules, V1  e.
i. Look for V1 on right side of the arrow of all the rules.
ii. Replace these V1 by e in all possible way, whatever string
comes as a result, add them to the same rule using OR “|”.
3. Remove all unit rules, V1  V2.
i. Look for the rule R for V2.
ii. Replace the V2 of the unit rule by right side of the arrow of R.
4. Convert all rules to CNF rule format, V1  V2V3, V1  t.
i. Introduce new rules with new variables to convert the
existing non-CNF rules to CNF rules.
ii. Try to have these new rules in the CNF format.
CNF Conversion:
Step 1:
Adding new
start variable S0.
Step 2:
S0  S
S  ASA | aB
A  B | S
B  b | e
S0  S
S  ASA | aB | a
A  B | S | e
B  b | e
S0  S
S  ASA | aB | a
A  B | S | e
B  b
S0  S
S  ASA | aB
A  B | S
B  b | e
Remove B  e
Remove A  e
S0  S
S  ASA | aB | a
A  B | S | e
B  b
S0  S
S  ASA | aB | a | SA
A  B | S | e
B  b
S0  S
S  ASA | aB | a | SA | AS
A  B | S | e
B  b
S0  S
S  ASA | aB | a | SA | AS | S
A  B | S | e
B  b
S0  S
S  ASA | aB | a | SA | AS | S
A  B | S
B  b
S0  S
S  ASA | aB
A  B | S
B  b | e

19. 19
CSC3113: Theory of Computation
EXAMPLE: CONVERTING TO CNF
Original Grammar
S  ASA | aB
A  B | S
B  b | e
CNF: Rules Format
1. A variable substitute by
two variables
V1  V2V3
2. A variable substitute by
a single terminal
V1  t
3. Exception: the start
variable may have an
epsilon rule
S0  e
Conversion Steps:
1. Add a new start variable (substitute by old start variable).
2. Remove all epsilon rules, V1  e.
i. Look for V1 on right side of the arrow of all the rules.
ii. Replace these V1 by e in all possible way, whatever string
comes as a result, add them to the same rule using OR “|”.
3. Remove all unit rules, V1  V2.
i. Look for the rule R for V2.
ii. Replace the V2 of the unit rule by right side of the arrow of R.
4. Convert all rules to CNF rule format, V1  V2V3, V1  t.
i. Introduce new rules with new variables to convert the
existing non-CNF rules to CNF rules.
ii. Try to have these new rules in the CNF format.
CNF Conversion:
Step 3:
Remove S  S
Remove S0  S
Remove A  B
Remove A  S
S0  S
S  ASA | aB | a | SA | AS | S
A  B | S
B  b
S0  S
S  ASA | aB | a | SA | AS
A  B | S
B  b
S0  S
S  ASA | aB | a | SA | AS
A  B | S
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  B | S
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  B | S
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  b | S
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  b | S
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  b | ASA | aB | a | SA | AS
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  b | ASA | aB | a | SA | AS
B  b
S0  S
S  ASA | aB | a | SA | AS | S
A  B | S
B  b
S0  S
S  ASA | aB | a | SA | AS
A  B | S
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  B | S
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  b | S
B  b

20. 20
CSC3113: Theory of Computation
EXAMPLE: CONVERTING TO CNF
Original Grammar
S  ASA | aB
A  B | S
B  b | e
CNF: Rules Format
1. A variable substitute by
two variables
V1  V2V3
2. A variable substitute by
a single terminal
V1  t
3. Exception: the start
variable may have an
epsilon rule
S0  e
Conversion Steps:
1. Add a new start variable (substitute by old start variable).
2. Remove all epsilon rules of the form, V1  e.
i. Look for V1 on right side of the arrow of all the rules.
ii. Replace these V1 by e in all possible way, whatever string
comes as a result, add them to the same rule using OR “|”.
3. Remove all unit rules of the form, V1  V2.
i. Look for the rule R for V2.
ii. Replace the V2 of the unit rule by right side of the arrow of R.
4. Convert all rules to CNF rule format, V1  V2V3, V1  t.
i. Introduce new rules with new variables to convert the
existing non-CNF rules to CNF rules.
ii. Try to have these new rules in the CNF format.
CNF Conversion:
Step 4:
Add rule C  SA
Add rule D  a
Find non-CNF rules
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  b | ASA | aB | a | SA | AS
B  b
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  b | ASA | aB | a | SA | AS
B  b
C  SA
S0  AC | aB | a | SA | AS
S  AC | aB | a | SA | AS
A  b | AC | aB | a | SA | AS
B  b
C  SA
S0  AC | aB | a | SA | AS
S  AC | aB | a | SA | AS
A  b | AC | aB | a | SA | AS
B  b
C  SA
S0  AC | aB | a | SA | AS
S  AC | aB | a | SA | AS
A  b | AC | aB | a | SA | AS
B  b
C  SA
D  a
S0  AC | DB | a | SA | AS
S  AC | DB | a | SA | AS
A  b | AC | DB | a | SA | AS
B  b
C  SA
D  a
S0  AC | DB | a | SA | AS
S  AC | DB | a | SA | AS
A  b | AC | DB | a | SA | AS
B  b
C  SA
D  a
S0  ASA | aB | a | SA | AS
S  ASA | aB | a | SA | AS
A  b | ASA | aB | a | SA | AS
B  b

21. 21
CSC3113: Theory of Computation
EXAMPLE-2
Original CFG
S  bS | aT | 
T  aT | bR | 
R  bS | 
Add new Start Variable P
P  S
S  bS | aT | 
T  aT | bR | 
R  bS | 
Remove R  
P  S
S  bS | aT | 
T  aT | bR |  | b
R  bS
Remove T  
P  S
S  bS | aT |  | a
T  aT | bR | b | a
R  bS
Remove S  
P  S | 
S  bS | aT | a | b
T  aT | bR | b | a
R  bS | b
Remove P  S
P  bS | aT | a | b | 
S  bS | aT | a | b
T  aT | bR | b | a
R  bS | b
Find rules not in CNF
format
P  bS | aT | a | b | 
S  bS | aT | a | b
T  aT | bR | b | a
R  bS | b
Add new Rules to convert the
rules not in CNF format
P  BS | AT | a | b | 
S  BS | AT | a | b
T  AT | BR | b | a
R  BS | b
A  a
B  b
Finally, in CNF format
P  BS | AT | a | b | 
S  BS | AT | a | b
T  AT | BR | a | b
R  BS | b
A  a
B  b

22. 22
CSC3113: Theory of Computation
EXAMPLE-3
Convert CFG to CNF
Original CFG
S  aXbX
X  aY | bY | 
Y  X | c

23. 23
REFERENCES
CSC3113: Theory of Computation
CONTEXT FREE LANGUAGE & GRAMMAR
Introduction to Theory of Computation, Sipser, (3rd ed),
CFL-2; All Exercises.
Elements of the Theory of Computation, Papadimitriou (2nd ed),
CFL-2.