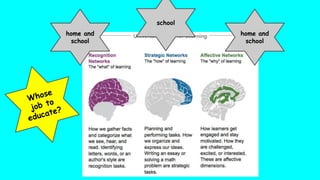
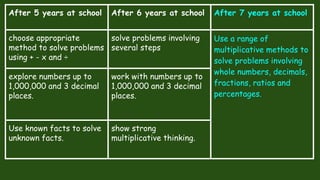
The document discusses the changing nature of mathematics education from the past to the present. It notes that students now need to be resilient, resourceful, creative, and innovative to solve the complex problems of the future. It contrasts how math was taught in the past, with an emphasis on individual work, memorization, and fear of mistakes, to how it is now taught, focusing on collaboration, celebrating mistakes as learning opportunities, and relating math to real world examples.