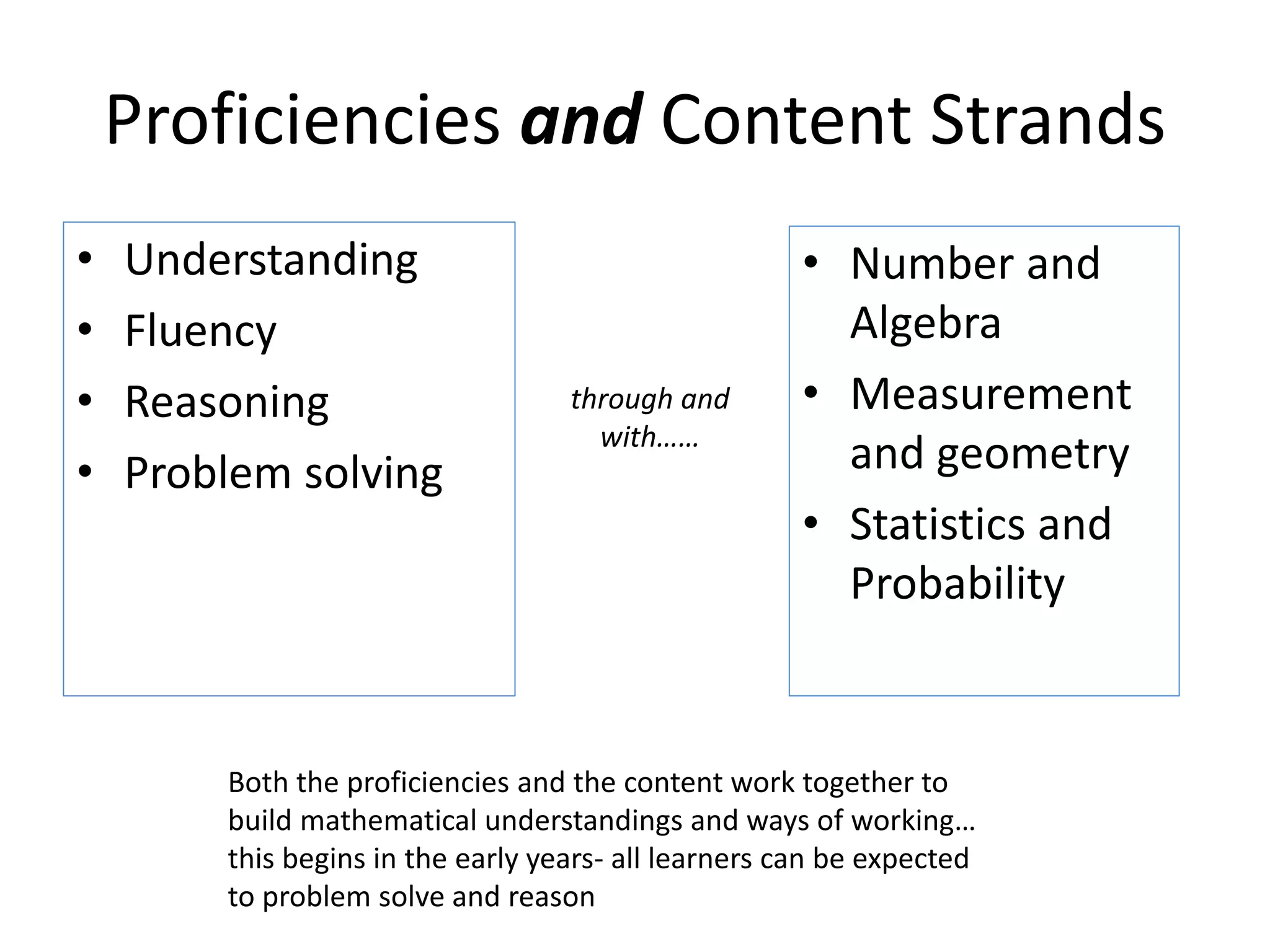
The document emphasizes the critical role of talk in promoting mathematical understanding in young learners, highlighting that effective communication enhances learning and problem-solving skills. It outlines strategies for educators to facilitate math discussions and develop students' mathematical vocabulary through collaborative learning. Additionally, it discusses the need for assessment through conversation to gauge children's understanding and reasoning in mathematics.

1. The Importance of Talk for
Mathematical Learning in the Early
Years
Denise Neal
November, 2014
Image sourced from:
http://docs.education.gov.au/system/files/doc/other/belonging_being_and_becoming_the_early_years_learning_framework_for_australia.pdf

2. Everyday Learning about Maths and
Numeracy
http://www.aamt.edu.au/Webshop/Newest-resources/Maths-and-Numeracy
http://www.earlychildhoodaustralia.org.au/shop/product/everyday-learning-about-maths-and-numeracy/

3. Key Message from the book
If we talk about mathematics and numeracy and show
positive attitudes to using their ideas to solve everyday
problems, children will want to learn more about it and
understand that learning isn’t always easy, but when we
solve problems and get past the confusion, we have the
satisfaction of learning something new.
When children tackle new challenges with appropriate
levels of support, they develop as curious, persistent,
highly engaged and successful learners. ….
Talk supports and extends this learning

4. Introduction
Overview
• The importance of talk
• Links to curriculum frameworks
• Promoting talk in the learning environment
(strategies and prompts)
• Talk as way to assess student learning
• References/resources
• Conclusion
• Questions

5. Source: Tracey Muir webinar- Connect with Maths, August 26th, 2014

6. Talk is Important!
• Research clearly tells us that oral language is
crucial for learning and that oral language is the
key to reading success. This involves not only
speaking but also the capacity to listen (PALL)
• Vocabulary is another foundation for reading and
learning. In the case of mathematics, there is a
wealth of vocabulary specific to the learning area
that helps build understanding and enables
learners to explain, justify and extend their
thinking.

7. Talk Matters
Klibanoff and colleagues discovered that teacher-facilitated
“math talk” in the early years significantly increased children’s
growth in understanding of mathematical concepts (2006, p.
59).
Knowledgeable educators recognize that although young
children may have a beginning understanding of mathematical
concepts they often lack the language to communicate their
ideas. By modelling and fostering math talk throughout the
day and across various subject areas, educators can provide
the math language that allows students to articulate their
ideas. It is also important to encourage talk among students as
they explain, question and discuss their strategies while
co-operatively solving problems.
http://www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/cbs_maximize_math_learning.pdf

8. Examples…
http://www.earlychildhoodaustralia.org.au/nqsplp/wp-content/uploads/2012/05/EYLFPLP_E-Newsletter_
No22.pdf
http://www.dreamstime.com/royalty-free-stock-photo-rolling-out-dough-pizza-child-making-fresh-beginning-image35196585

9. Curriculum
Both the Early Years Framework for Australia
and the Australian Curriculum value and
promote the importance of communication.

10. The EYLF
..educators are also responsive to children’s
ideas and play, which form an important basis
for curriculum decision-making. In response to
children’s evolving ideas and interests,
educators assess, anticipate and extend
children’s learning via open ended questioning,
providing feedback, challenging their thinking
and guiding their learning. They make use of
spontaneous ‘teachable moments’ to scaffold
children’s learning.

11. Australian Curriculum
http://www.australiancurriculum.edu.au/mathematics/Curriculum/F-
10?layout=1

12. Proficiencies and Content Strands
• Understanding
• Fluency
• Reasoning
• Problem solving
• Number and
Algebra
• Measurement
and geometry
• Statistics and
Probability
through and
with……
Both the proficiencies and the content work together to
build mathematical understandings and ways of working…
this begins in the early years- all learners can be expected
to problem solve and reason

13. Building Dispositions
…enduring habits of mind and actions, and
tendencies to respond in characteristic ways to
situations, for example, maintaining an
optimistic outlook, being willing to persevere,
approaching new experiences with confidence.
(Carr, 2001)

14. Reasoning
Reasoning mathematically is a habit of mind, and like all habits, it must be
developed through consistent use in many contexts.
From children's earliest experiences with mathematics, it is important to help
them understand that assertions should always have reasons. Questions such
as "Why do you think it is true?" and "Does anyone think the answer is
different, and why do you think so?" help students see that statements need to
be supported or refuted by evidence. Young children may wish to appeal to
others as sources for their reasons ("My sister told me so") or even to vote to
determine the best explanation, but students need to learn and agree on what
is acceptable as an adequate argument in the mathematics classroom. These
are the first steps toward realizing that mathematical reasoning is based on
specific assumptions and rules.
http://www.fayar.net/east/teacher.web/math/standards/document/chapter3/reas.htm

15. Mathematizing
The educator can play an integral role by making
meaningful connections between the mathematical
strands, the real world and other disciplines, and most
importantly, “between the intuitive informal mathematics
that students have learned through their own
experiences and the mathematics they are learning in
school” (For example, as a child naturally creates and
extends a pattern while making a necklace, the educator
can effectively pose questions that provoke the student
not only to describe the pattern, but also to make
predictions and generalizations).
http://www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/cbs_maximize_math_learning.pdf

16. The importance of discussion
Research has shown, however, that “manipulatives
themselves do not magically carry mathematical
understanding. Rather, they provide concrete ways
for students to give meaning to new knowledge”
Students need the opportunity to reflect upon their
actions with manipulatives, and through discussion,
articulate the meaning they generate, so that the
link between their representations and the key
mathematical ideas is apparent
(Clements & Sarama, 2009, p. 274).

17. Pause and talk…
• Questions?
• Comments?
• Your experiences?

18. Talking AND Listening
We have a lot of talk and attention to speaking and listening
and while many classrooms have gone a long way to
improving children’s speaking in mathematics lessons, I think
we still have a way to go in promoting deep listening (Askew,
2012)
Classrooms can support student learning by ensuring that
solutions proposed by students are built on.
Collective mathematical meaning is built when teachers
carefully listen to students and select solutions to be shared
which will build and develop collective understanding.

19. Supporting maths talk
Suzanne Chapin proposes five effective talk moves which
help to create meaningful mathematics discussions.
Revoicing is one move that is particularly useful when a
student’s explanation is confusing or hard for others to
understand. The teacher repeats all or some of what the
child said and then asks for clarification, which in turn
provokes the child to clarify and offer further explanation.
This also gives the educator an opportunity to embed
mathematics vocabulary so the child can further explain
his/her thinking (2009, p. 14).
http://www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/cbs_maximize_math_learning.pdf

20. A recommended read
Askew, M (2012) Transforming Primary Mathematics, Milton Park, UK:
Routledge.

21. A recommended read

22. Supporting Maths Talk- Talk Moves
http://www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/cbs_maximize_math_learning.pdf

23. Building talk
• Making sense of problems by explaining them to
someone else, putting them into your own words
and comparing your answers with others all helps
meaning to emerge.
• Talking mathematics means that mathematical
vocabulary becomes part of the classroom
discourse- much more than a list of words!
Askew, M (2012) Transforming Primary Mathematics, Milton Park, UK: Routledge

24. Our actions and interactions are key
Responsive learning
relationships are
strengthened as educators
and children learn together
and share decisions, respect
and trust. Responsiveness
enables educators to
respectfully enter children’s
play and ongoing projects,
stimulate their thinking and
enrich their learning.
Image sourced from:
http://www.earlychildhoodaustralia.org.au/nqsplp/wp-content/
uploads/2012/05/EYLFPLP_E-Newsletter_No22.pdf

25. Planning for talk
• Maths talk time- turn to your maths talk
partner and chat about this (as problems are
posed, during the lesson and at the end)
• Sharing or reflection time- built into the
planning of a lesson (not always at the end of
the lesson)
• Plan for explicit teaching and use of subject
specific vocabulary in each sequence

26. What do we do to promote good
maths talk?
1. Try to use tasks that engage the pupils in thinking for themselves and allow you to
work alongside them on occasions.
2. Find time to listen and communicate with pupils as they work on these tasks.
3. Try to avoid controlling the communication to get to a mathematical end that you
have predetermined but encourage mathematical thinking instead. "Go with the flow.“
4. Wait at least 5 seconds for a response before speaking further.
5. Help pupils to speak and listen to each other in a constructive way.
6. Do not make assumptions.
7. Watch body language and voice intonation in order to minimise a power imbalance.
http://nrich.maths.org/6662

27. Asking Open Questions
http://www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/cbs_askingeffectivequestions.pdf

28. Building a Learning Culture
Learning cultures either promote or constrain
talk…

29. Tasks
Tasks either promote or constrain talk…carefully
select tasks for a mathematical purpose.
http://nrich.maths.org/content/id/8863/Incey%20Wincey.pdf

30. Use Props and Prompts for Talk
http://www.dreamstime.com/stock-photography-toy-microphone-close-up-image18830572

31. Props

32. Props

33. Props

34. Prompts

35. Prompts

36. Books can prompt and extend
mathematical talk

37. Vocabulary is Important
We support children’s mathematical vocabulary
development by:
• Using and modelling correct mathematical
language
• Planning for the language required in units of
work/lessons
• Expecting children to use correct
mathematical language

38. Vocabulary

39. ICTs can prompt and extend talk

40. Capturing Talk Informs our Work
http://postmediacalgaryherald.files.wordpress.com/2012/03/ipad.jpg
Talk becomes evidence of learning or misconceptions in children’s learning.
Capturing childrens’ talk enables us as educators to gather evidence to share
with parents and others. Technology enables us to easily capture talk- smart
phones, ipads and other devices enable us to record audio and/or video files in
ways that were not possible in the past.

41. Talk is important for assessment
We once thought that it was what children could
put on paper that mattered. We made
assessment decisions based on this. We now
know that we need to value and promote talk as
a way of both communicating and assessing
mathematical understanding.

42. Talking to assess
We learn so much about what children know, understand
and are able to do through interacting with them and
listening to their explanations. Many assessment tools
such as
Count Me in Too http://www.curriculumsupport.education.nsw.gov.au/countmein/assesment.html
The Early Years Numeracy Interview
https://www.eduweb.vic.gov.au/edulibrary/public/teachlearn/student/mathscontinuum/onlineinterviewbklet.pdf
Assessment for Common Misunderstandings
http://www.education.vic.gov.au/school/teachers/teachingresources/discipline/maths/assessment/pages/misunderstandings.aspx
Use talk and one-on-one interviews to assess childrens’
mathematical thinking. Such opportunities provide a
window into childrens’ thinking as they explain their
answers and the processes they have used.

43. Assessing through talk
Formal interviews are not necessary though, as
informal discussions, overheard conversations
and effective questions from adults can also
provide valuable information about childrens’
thinking, reasoning and understanding of
mathematical ideas.
Image: http://www.childhoodnannies.com/teachers-presents/

44. Our Aim: Mindful mathematics
learning
In mindful mathematics lessons the shift is to:
- Someone explaining
- Everyone following the explanation
- It’s not that the teacher never explains, but
that everyone in the community gets to be the
teacher and learner, whether they are adult or
child.

45. Conclusion
Good maths classrooms are talking classrooms!
Effective talk requires thoughtful planning and careful
listening
Students should be expected to reason and explain from the
early years and can be assessed on their capacity to reason
and justify using mathematical language.
The mathematical proficiencies help us to plan for tasks , to
make assessment judgements and to build mathematical
behaviour and dispositions.

46. Conclusion
One of the most valuable ways
an educator can support young
children’s developing numeracy
is to provide the language to
talk about maths and
mathematical ideas. That
means that educators need to
understand mathematical
concepts and to recognise the
potential of situations for rich
numeracy learning .
http://www.earlychildhoodaustralia.org.au/nqsplp/wp-content/
uploads/2012/05/EYLFPLP_E-Newsletter_No22.pdfeveryday
Keep on talking!
Image sourced from:
http://www.earlychildhoodaustralia.org.au/nqsplp/wp-content/
uploads/2012/05/EYLFPLP_E-Newsletter_No22.pdf

47. Useful References
Australian Government Department of Education, Employment and Workplace Relations (2007)Early Childhood Literacy and
Numeracy- building good practice, http://www.vcaa.vic.edu.au/documents/earlyyears/buildinggoodpractice.pdf (accessed August
26, 2014)
Early Childhood Australia (2011) Being Numerate: Early Years Learning Framework Professional Learning, Newsletter 22
http://www.earlychildhoodaustralia.org.au/nqsplp/wp-content/uploads/2012/05/EYLFPLP_E-Newsletter_No22.pdf (Accessed
August 26, 2014)
Ontario Ministry of Education, Student Achievement Division, Capacity Building Series, Special edition 22, Maximizing Student
Mathematical Learning in the Early Years (2011)
http://www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/cbs_maximize_math_learning.pdf (accessed August 26, 2014)
Ontario Ministry of Education, Student Achievement Division, Capacity Building Series, Special edition 21, Asking Effective
Questions (July, 2011)
http://www.edu.gov.on.ca/eng/literacynumeracy/inspire/research/cbs_askingeffectivequestions.pdf
Building Mathematical Competencies in Early Childhood https://www.youtube.com/watch?v=iVFP-4iw_r4
https://www.youtube.com/watch?v=BMoF-hiH3J8
https://www.youtube.com/watch?v=rsKNrnlfXt4&list=PLVVQEyDnsoWVRYxJSIO3RoET9R0P1gtcx&index=3
https://www.youtube.com/watch?v=xssBJpOBecs&list=PLVVQEyDnsoWVRYxJSIO3RoET9R0P1gtcx&index=4
https://www.youtube.com/watch?v=WVfwBQe_IJE&list=PLVVQEyDnsoWVRYxJSIO3RoET9R0P1gtcx&index=5
https://www.youtube.com/watch?v=1IjesoJJTp0
Five Practices for Orchestrating Productive Mathematics Discussions (Smith & Stein)
http://www.aamt.edu.au/Webshop/Newest-resources/Five-Practices
http://nrich.maths.org/early-years Nrich early years site