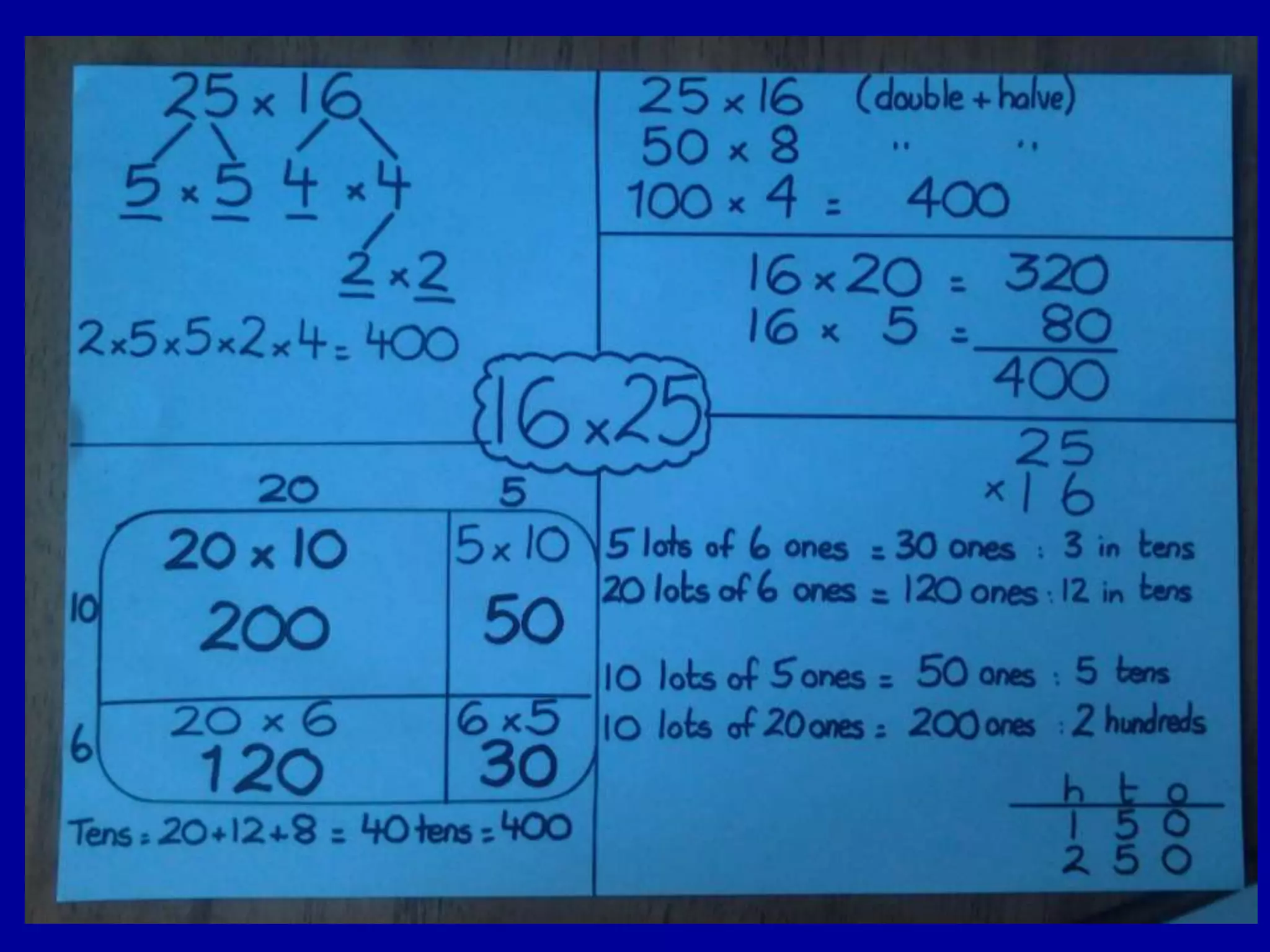
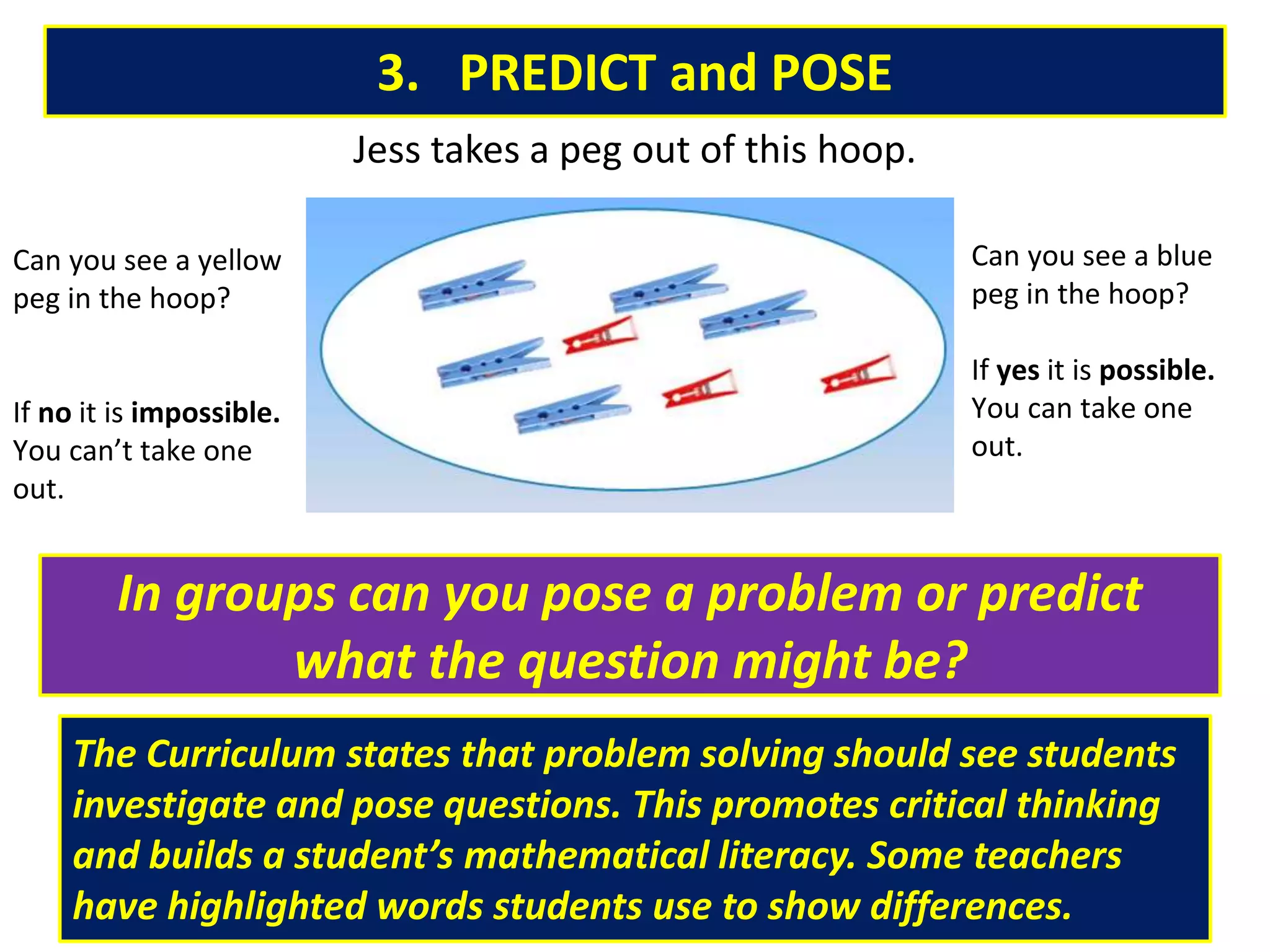
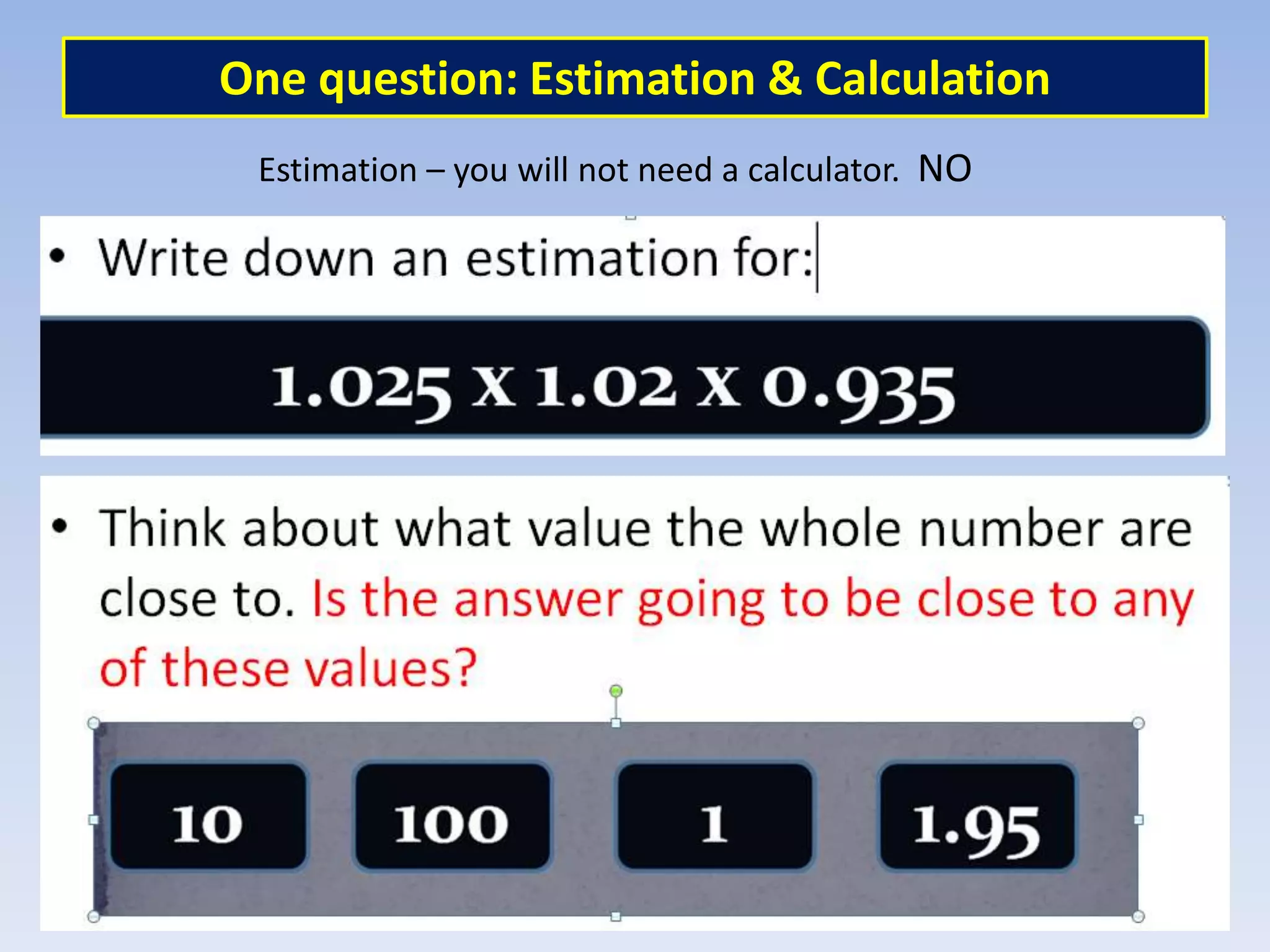
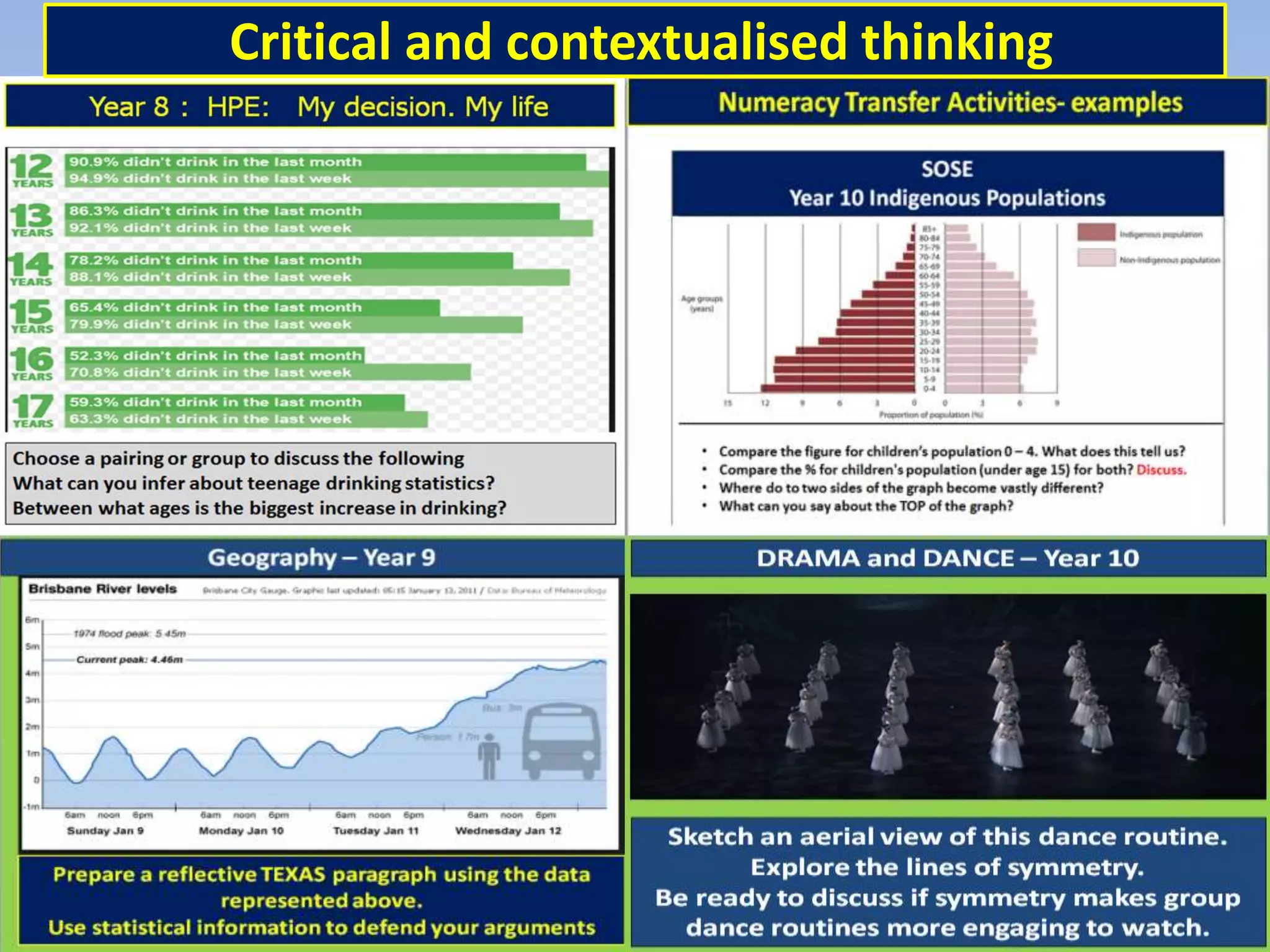
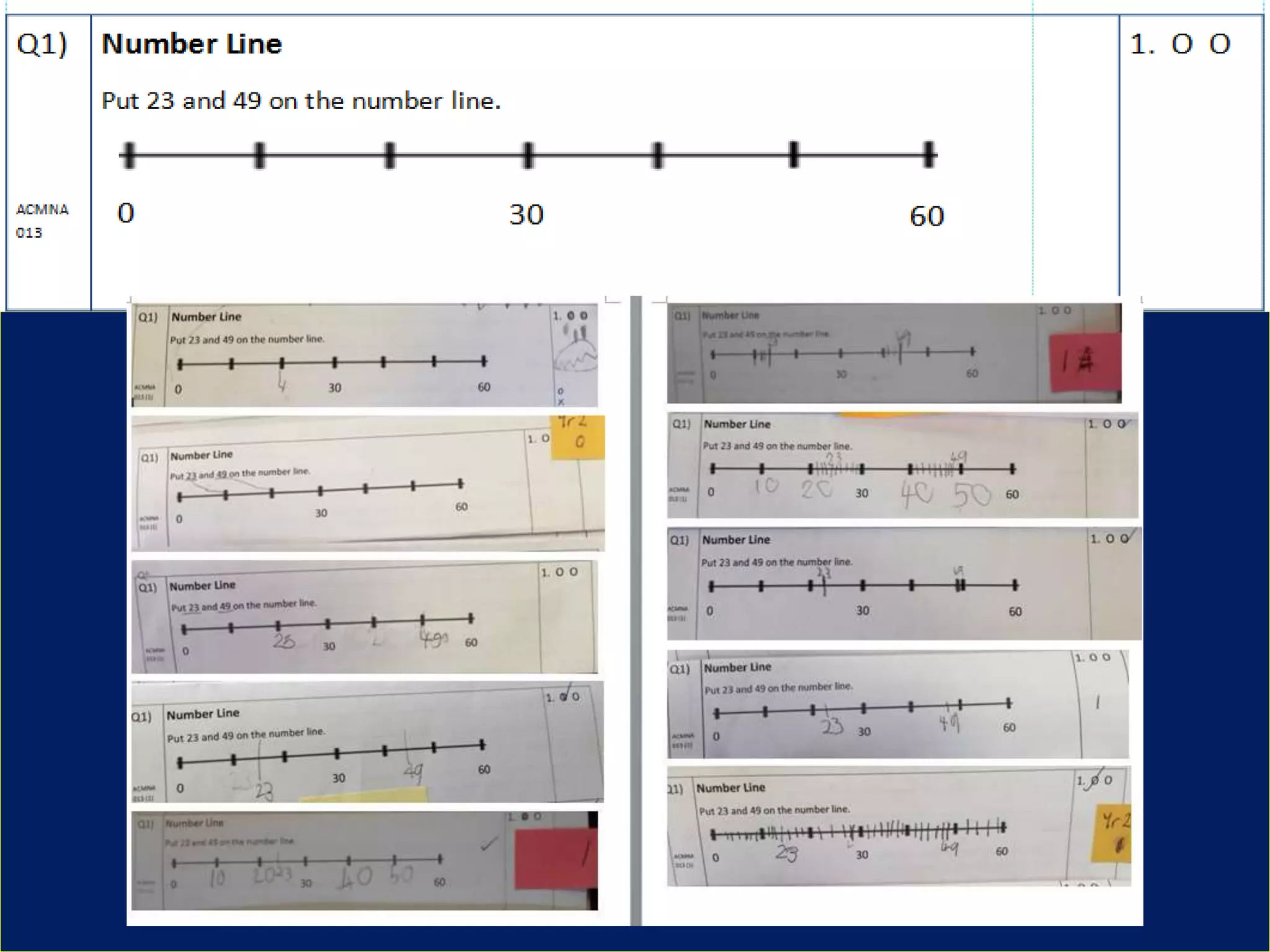
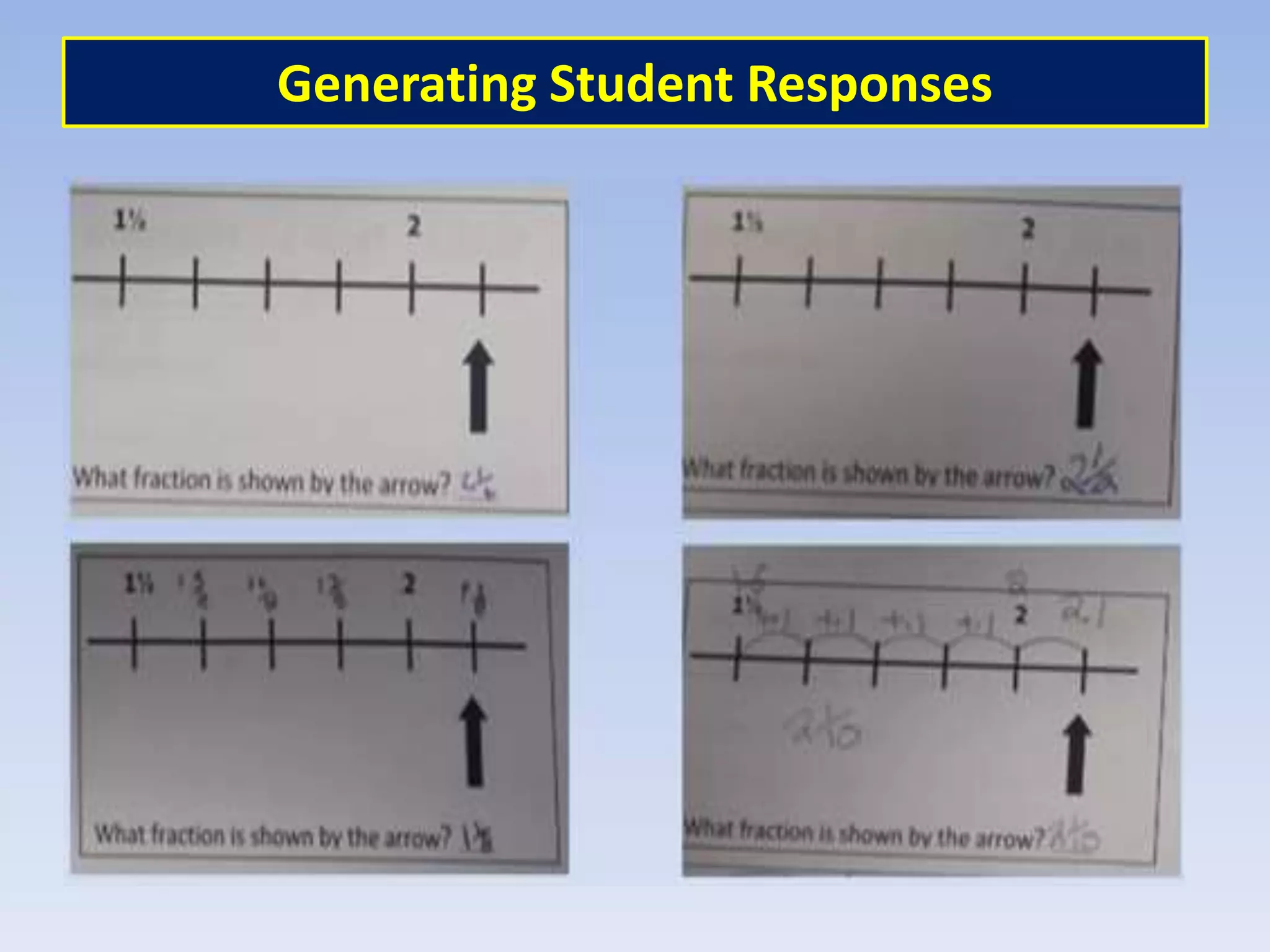
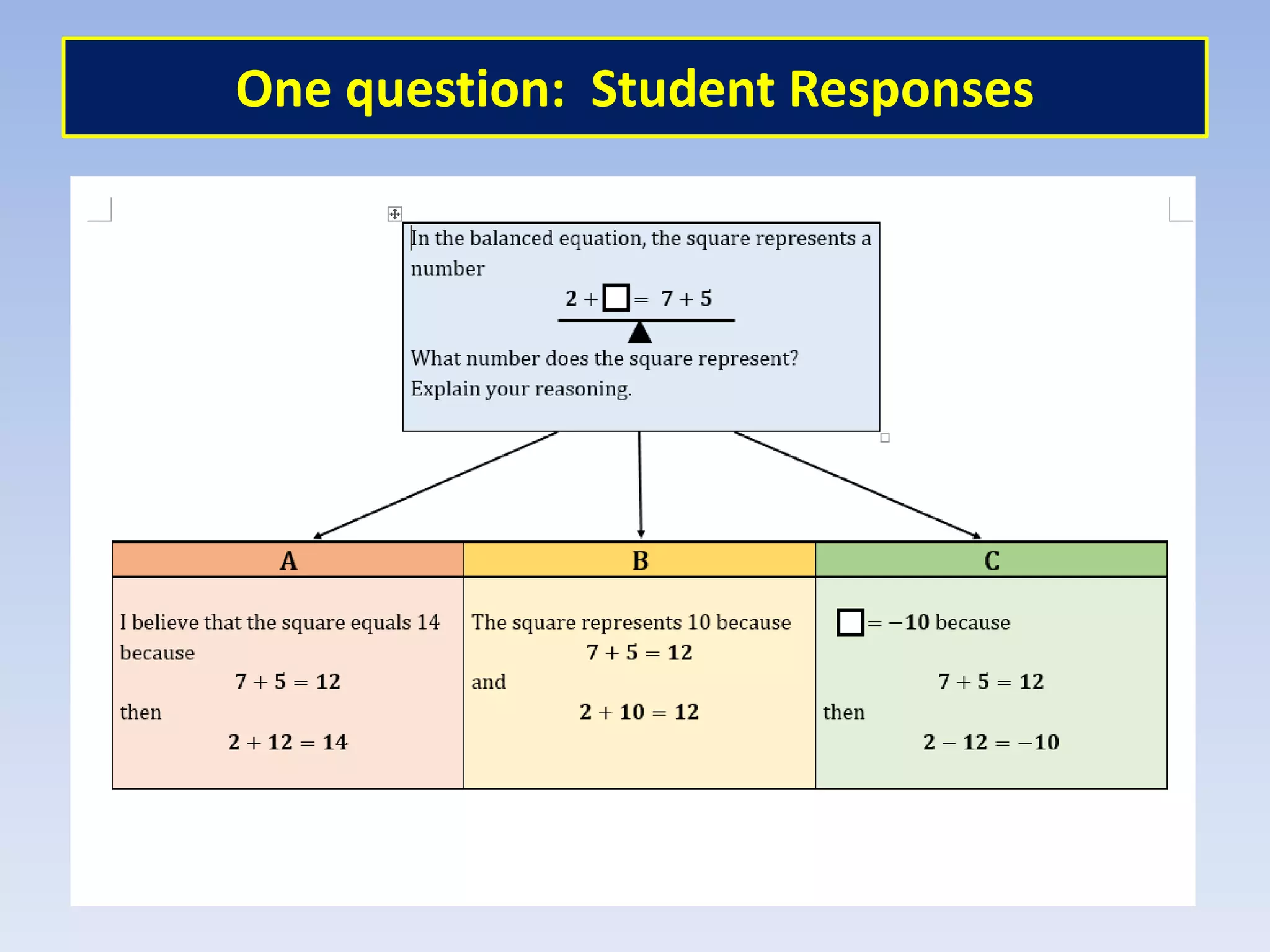
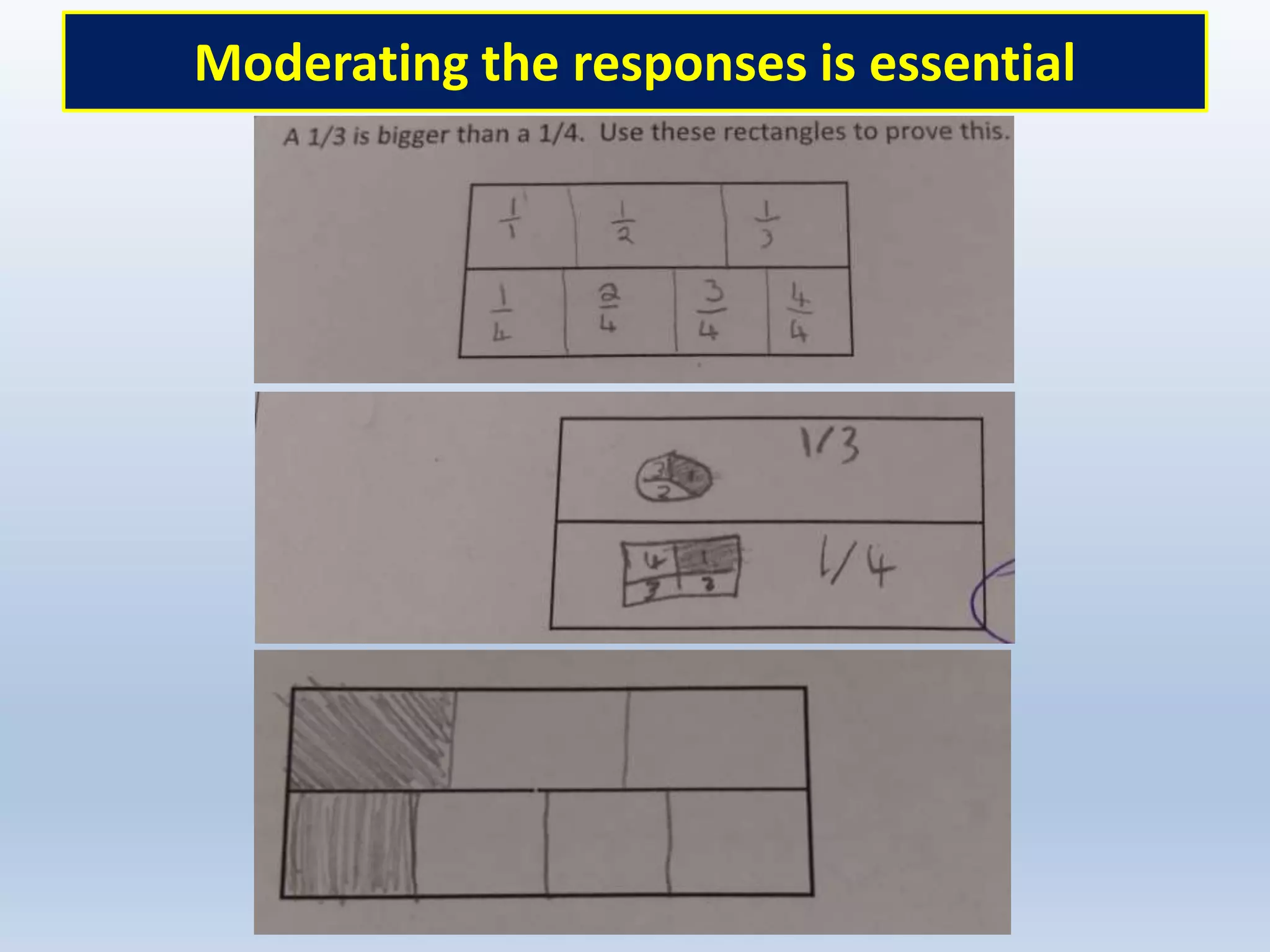
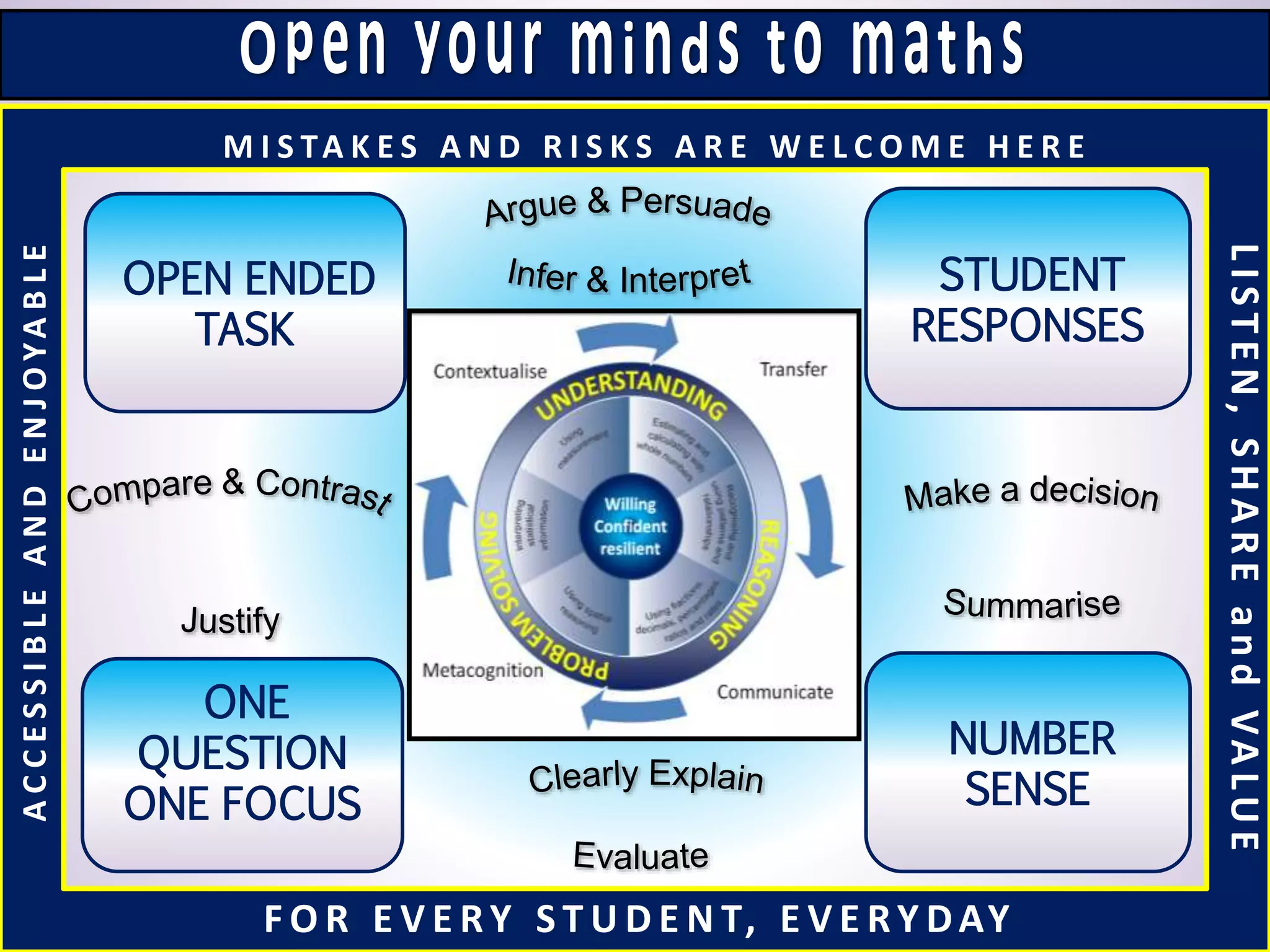
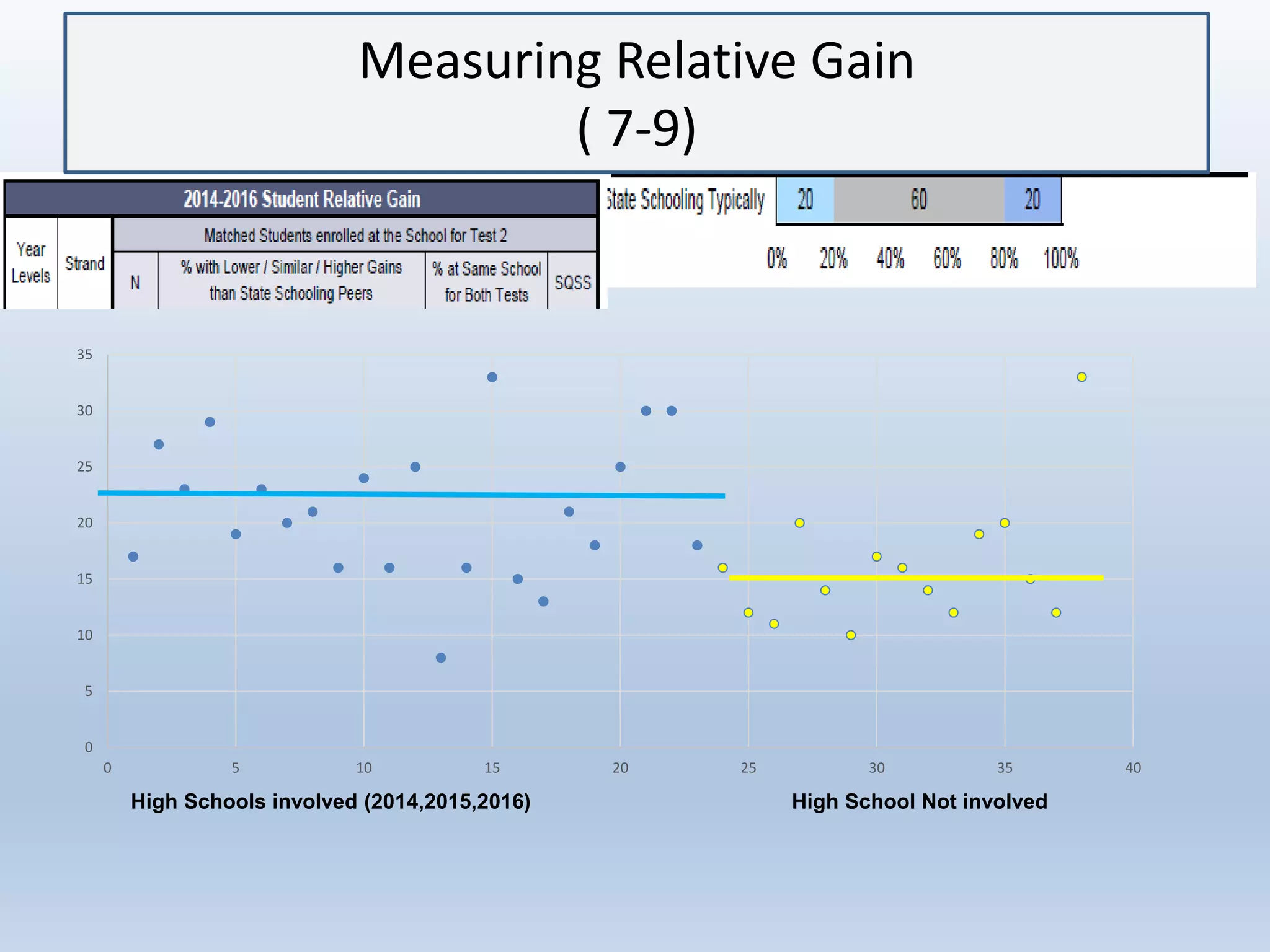
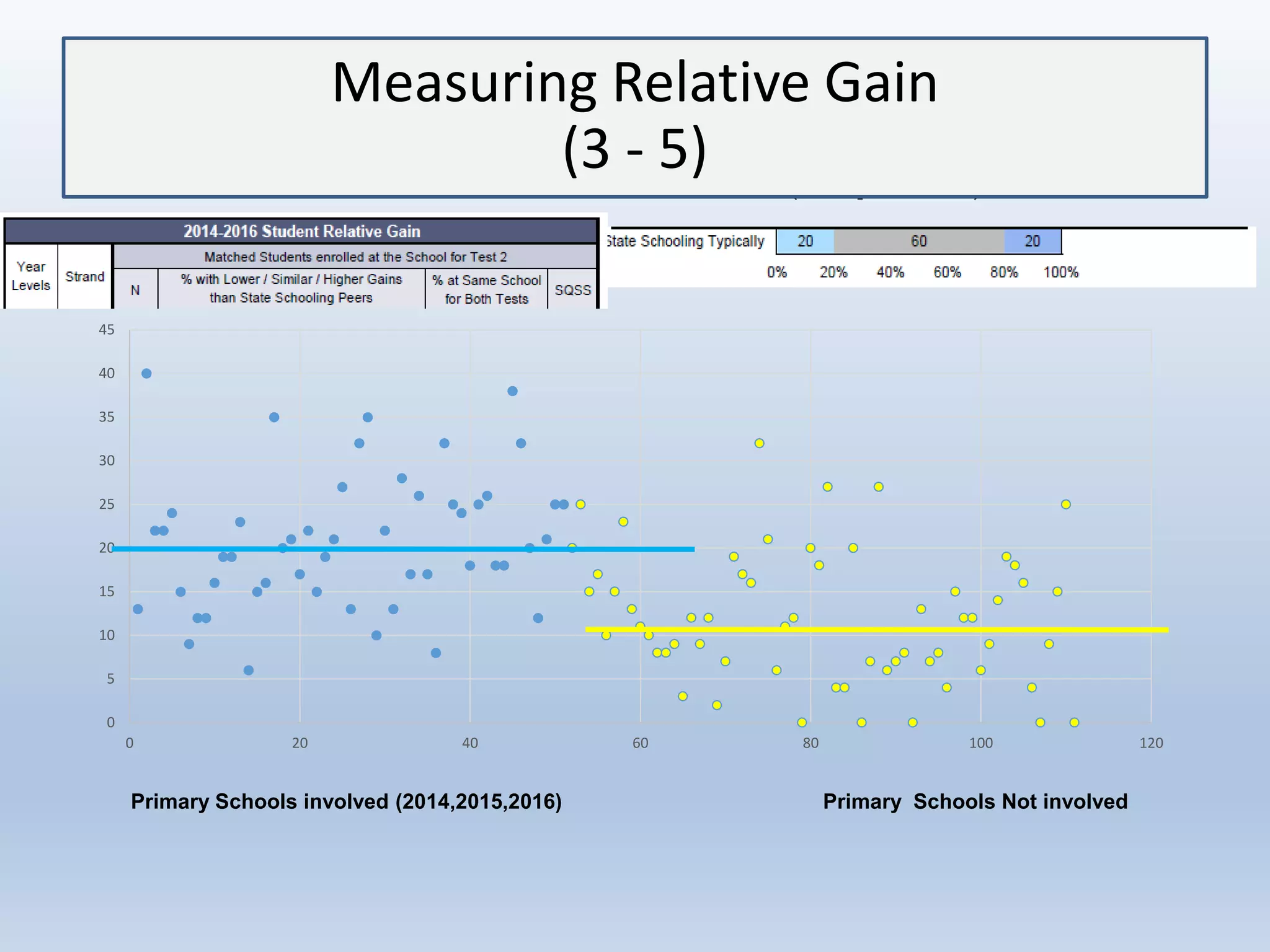
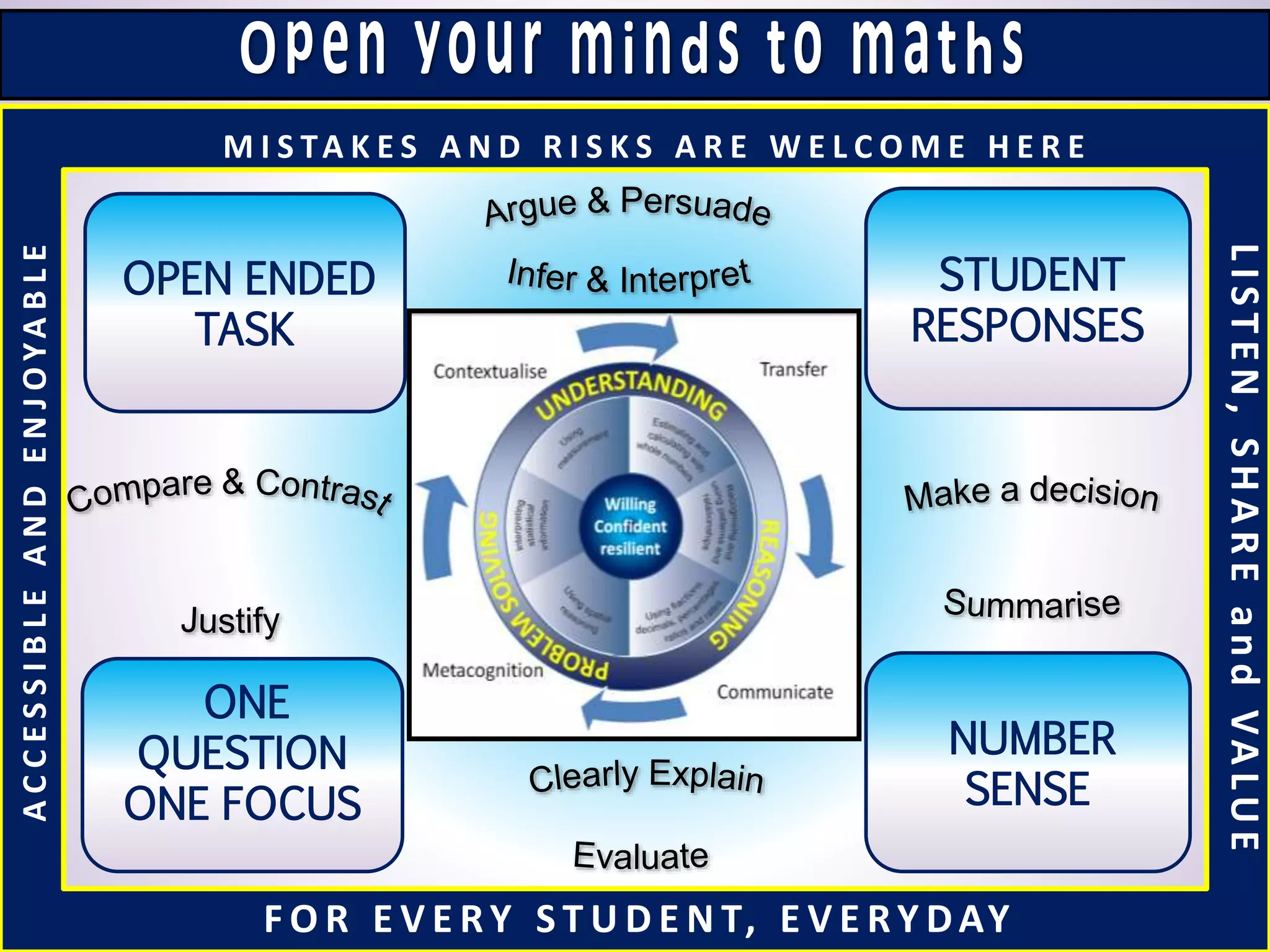
This document discusses the implications of beliefs and knowledge on the understanding of fractions and numeracy education among students and teachers. It highlights the importance of number sense activities and critical thinking in enhancing students' mathematical abilities, emphasizing open-ended questions and peer discussions for deepening knowledge. Additionally, it reflects on the effectiveness of diagnostic assessments and the significance of collaboration among educators to improve math learning experiences.

2. Session 3: Right Knowledge

3. The implications of beliefs and knowledge on
resources
Shade in a fraction of a shape
which already has been broken
into equal parts.
Identify fraction of a group using
lines, circles
Naming parts of a fraction
Count on or back in 1s, 10s from
multiples of 10,100
Identify value of each digit
Make biggest number
Expanding numbers
Writes in digits and words
Right or Wrong
Add up ticks to
make judgement
65% did not
recognise or value
understanding in
the standards
Throughout 2015 and 2016, 175 teachers illustrated their
belief and understanding of the Achievement Standard

4. A ‘C’ level is beyond just recall of rehearsed
procedures
Identifies fraction of shape
Identifies fraction of collection
Name, understand a fraction
Locates on a number line
Represent as part of whole
Explains the use of fractions in
everyday life
Recognise & read numbers from
digits up to 10 000
Models 4 digit numbers
Adds, takes 1s, 3s, 10s from 4-
digit numbers
Create and explain patterns of
their own
Right or Wrong
Add up ticks to
make judgement
Varied responses.
Consistency via
moderation and
annotations.
Right ≠ full marks
The ACARA work samples can help teachers understand
the requirements for a satisfactory level.

5. OPEN ENDED
TASK
ONE
QUESTION
ONE FOCUS
F O R E V E RY S T U D E N T, E V E RY DAY
ACCESSIBLEANDENJOYABLE
M I S TA K E S A N D R I S K S A R E W E L C O M E H E R E
LISTEN,SHAREandVALUE
STUDENT
RESPONSES
NUMBER
SENSE

6. Activities: Number Sense

7. NUMBER FACTS STORY
( drawing or oral )
A chef made 10 cakes and I
ate 2 of them. There are 8
cakes left
RELATED FACTS EXTENDED FACTS
If I know 8 + 2 = 10
then I also know:-
80 + 20 = 100
100 – 20 = 80
Remember to emphasise unknown PARTS
100 – [ ] = 80 [ ] – 8 = 2 8 + [ ] = 10
8 + 2 = 10
2 + 8 = 10
10 - 8 = 2
10 – 2 = 8
OPEN ENDED Yr1-6

9. Whose story is it?
7 = 3 + 3 + 1
7 = 3 + [ ] + 1
What is the missing number?
How can we prove it?
Commutative and
Associative
Properties
Match the beads
with the symbolsModel a story on
the beads as it is
read out

10. A Adds in order 7,5,3,5 and then 6 all on fingers
B Colours in grid squares in their grid book and counts all
C Says 7 and 3 make 10, 5 and 5 make 10 and 6 more is 26
D Says 5+5 = 10 , then 6 + 3 = 9 so 19 and counts on the 7
E Takes 2 from 7 and adds it the 3 to make 4 x 5 = 20 + 6
F Says 7 + 5 = 12 and 6 + 5 = 11. writes them down . Adds 3
26 = 7 + 5 + 3 + 5 + 6
Numeracy requires Number Sense Yr 1 and 2

11. Students in conceptually orientated classes for
mathematics out perform those in a procedurally
orientated class in tests, attitudes and disposition
towards maths
Cain 2002 Masden & Lainer 92 Fuson et al 2000
Numeracy requires Number Sense Yr 5 and 6

13. Activities: Cognitive Activation
Tasks

14. Deepening Knowledge Yr4
• Place your numbers on a number line and be ready to
defend your positioning using benchmarks
• With the five digits you rolled, make the third largest number
you can and be ready to defend your decision

15. More examples Yr4

16. Rob Proffitt-White NCR: August 2016

17. One question: Routines for reasoning

18. 1. DISCUSS and DEFEND
With your elbow partner decide on an answer
and be ready to clearly explain your choice
Can they prove their decision by representing the amounts with
0-99 board, bundling sticks, beads, place value houses etc

19. 2. DESTROY the DISTRACTOR
In pairs can you find a wrong answer and prove
it is wrong to the class
A B C D
1, 3, 5, 7 8, 10, 12, 14 2, 4, 5, 7 20, 40, 60,80

20. 3. PREDICT and POSE
In groups can you pose a problem or predict
what the question might be?
The Curriculum states that problem solving should see students
investigate and pose questions. This promotes critical thinking
and builds a student’s mathematical literacy. Some teachers
have highlighted words students use to show differences.
Jess takes a peg out of this hoop.
Can you see a blue
peg in the hoop?
If yes it is possible.
You can take one
out.
Can you see a yellow
peg in the hoop?
If no it is impossible.
You can’t take one
out.

21. One question: Reason and Communicate
In pairs choose an answer you think is
unreasonable. If our can clearly communicate
your reasoning it will be destroyed

22. Estimation – you will not need a calculator. NO
One question: Estimation & Calculation

23. Critical and contextualised thinking

24. Activities: Student Feedback

26. Generating Student Responses

27. One question: Student Responses

28. Rob Proffitt-White NCR: March 2015
Moderating the responses is essential

29. OPEN ENDED
TASK
ONE
QUESTION
ONE FOCUS
F O R E V E RY S T U D E N T, E V E RY DAY
ACCESSIBLEANDENJOYABLE
M I S TA K E S A N D R I S K S A R E W E L C O M E H E R E
LISTEN,SHAREandVALUE
STUDENT
RESPONSES
NUMBER
SENSE

30. Influential Support for Initiative
I was most impressed by the
diagnostic assessments that have
been developed, in particular the
focus on the proficiencies is
exemplary .
I was also impressed with the
attention to detail in the moderating
process, the associated diagnosis
and the feedback given to students.
Your team's set of resources is the
most practical and comprehensive set
of supports for the implementation of
the Australian Curriculum: Mathematics
that I have ever seen.
2015 2016
It is an outstanding example of “grass roots” collaboration and initiative to improve
the experience of learning mathematics. It is a model that can be used by clusters
generally.

31. Sustaining the sense of Urgency
The Region The Schools The Key Team
Clear lines of sight
Influential Experts
Long term goals
Long term
commitment
Funding Coaches,
TRS
Networking
Support & Mentor
Valued contributions
Confident &
Passionate
Visibility. Commitment. Ownership

32. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35 40
High Schools involved (2014,2015,2016) High School Not involved
Measuring Relative Gain
( 7-9)

33. 0
5
10
15
20
25
30
35
40
45
0 20 40 60 80 100 120
Year 3 - 5 Relative Gain ( Top 20%)
Primary Schools involved (2014,2015,2016) Primary Schools Not involved
Measuring Relative Gain
(3 - 5)

34. Targets: Surface or Deep?
Student or School?
Our Initiative is about making the ‘Right Choice’ (Guy Claxton)
To get good results, AND
produce young people who are
passive, dependent and anxious
about failure
To get good results, AND
produce young people who are
inquisitive, imaginative and
independent
"It takes three to five years for change in practice to clearly
show up in a change in learning," he said. "Sometimes it can
take up to seven years to turn a school around.“
Peter Goss: Grattan Institute, August 2016