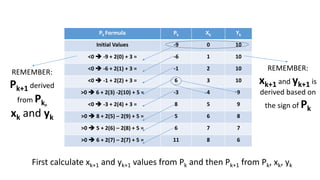
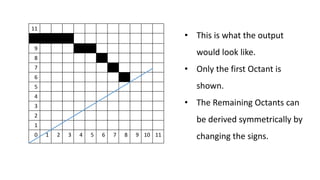
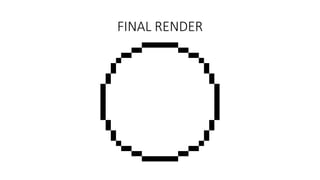
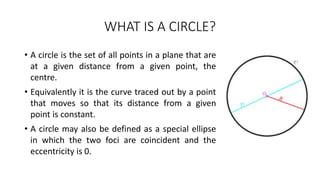
This document explains Bresenham's midpoint circle drawing algorithm. It defines a circle as all points equidistant from a center point. The algorithm uses integer arithmetic to iteratively determine the next pixel on the circle circumference. It starts at an initial point and calculates a decision parameter P to determine if the next point is above or below along the y-axis. It tabulates an example of drawing a circle of radius 10 centered at the origin to demonstrate how P is used to progress around the circle octant by octant.

1. BRESSENHAM’S MIDPOINT
CIRCLE DRAWING ALGORITHM
(EXPLAINED)

2. WHAT IS A CIRCLE?
• A circle is the set of all points in a plane that are
at a given distance from a given point, the
centre.
• Equivalently it is the curve traced out by a point
that moves so that its distance from a given
point is constant.
• A circle may also be defined as a special ellipse
in which the two foci are coincident and the
eccentricity is 0.

4. GENERATING CIRCLES
Circle equation : f(x,y) = x2 + y2 – r2
Any point on the circumference of the circle will satisfy the above
equation.
Hence :
>0  Point is outside the boundary of the circle
f(x,y) =0  Point is on the boundary of the circle
<=  Point is inside the boundary of the circle

5. FIRST OCTANT
• For a pixel at (xk, yk) the next pixel (xk +1, yk) or at (xk+1,
yk–1) is closer to the circle.
• The pixel point Pk for a corresponding point on the circle
is given as:
Pk = f(xk + 1, yk – ½) = (xk + 1)2 + yk - ½)2 – r2
• The next pixel point Pk+1 is given as:
Pk+1 = f(xk+1 + 1, yk+1 - ½) = [(xk + 1) + 1]2 + (yk+1 - ½ )2 – r2
(xk +1, yk)
(xk+1, yk–1)

6. Expanding Pk and Pk+1 and subtracting them, the eq. obtained is:
Pk+1 = Pk + 2(xk+1) + (y2
k+1 – y2
k) – (yk+1 – yk) + 1
(where the next Y – coordinate (yk+1) is either yk or yk-1 depending on
the sign of Pk.)
Since xk+1 denotes the next point along the X – axis (going rightwards)
xk+1 = xk + 1  2(xk+1) = 2xk + 2
Since yk+1 denotes the next point along the Y – axis (going downwards)
yk+1 = yk - 1  2(yk+1) = 2yk - 2

7. We’ve have to begin somewhere. So let the
starting position be (x0,y0) = (0, r)
Substituting these values in the circle
equation, P0 = f(1, r – ½) = 𝟓
𝟒 - r
Since r is a integer, neglecting the small
value of ¼, we have P0 = 1 - r
(0, r)
(0, 0)

8. BRESSENHAM’S ALGORITHM
1. Input radius r and centre of the circle (xc, yc), and obtain the first
point on the circumference of a circle centred on the origin as
(x0, y0) = (0, r)
2. Calculate the initial value of the decision parameter as
P0 = 1 – r
where r is the radius of the circle

9. 3. At each xk position, starting at k= 0, perform the following test:
If (Pk < 0), then the NEXT POINT along the circle centred on (0, 0) is
(xk+1, yk) and Pk+1 = Pk + 2xk+1 +1
 Pk+1 = Pk + 2xk + 3
Otherwise, the NEXT POINT along the circle is
(xk+1, yk–1) and Pk+1 = Pk + 2xk+1 + 1 – 2yk+1
 Pk+1 = Pk + 2xk – 2yk + 5
2xk+1 = 2xk + 2
2yk+1 = 2yk – 2

10. 4. Determine the Symmetry Points on the other 7 Octants
5. Move each calculated pixel position (x,y) onto the circular path
centered at (xc,yc) and plot the coordinate values as
x = x + xc and y = y + yc
6. Repeat steps 3 to 5 until x >= y

11. FOR EXAMPLE
Consider a circle that has to be drawn with its center at (0, 0) and a
radius of 10:
Initial point on the circumference of the circle is (0, r) = (0 ,10)
Initial pixel P0 = 1 – r = 1 – 10 = -9
Therefore, x = 0, y = 10, 2x = 0, 2y = 20, P0 = -9
Applying Bressenham’s Algorithm, we tabulate the data into a table

12. Pk Formula Pk Xk Yk
Initial Values -9 0 10
<0  -9 + 2(0) + 3 = -6 1 10
<0  -6 + 2(1) + 3 = -1 2 10
<0  -1 + 2(2) + 3 = 6 3 10
>0  6 + 2(3) -2(10) + 5 = -3 4 9
<0  -3 + 2(4) + 3 = 8 5 9
>0  8 + 2(5) – 2(9) + 5 = 5 6 8
>0  5 + 2(6) – 2(8) + 5 = 6 7 7
>0  6 + 2(7) – 2(7) + 5 = 11 8 6
REMEMBER:
xk+1 and yk+1 is
derived based on
the sign of Pk
REMEMBER:
Pk+1 derived
from Pk,
xk and yk
First calculate xk+1 and yk+1 values from Pk and then Pk+1 from Pk, xk, yk

13. 11
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 10 11
• This is what the output
would look like.
• Only the first Octant is
shown.
• The Remaining Octants can
be derived symmetrically by
changing the signs.

14. FINAL RENDER

15. Prepared by
Mrinmoy Dalal
13311A0506
S.N.I.S.T.