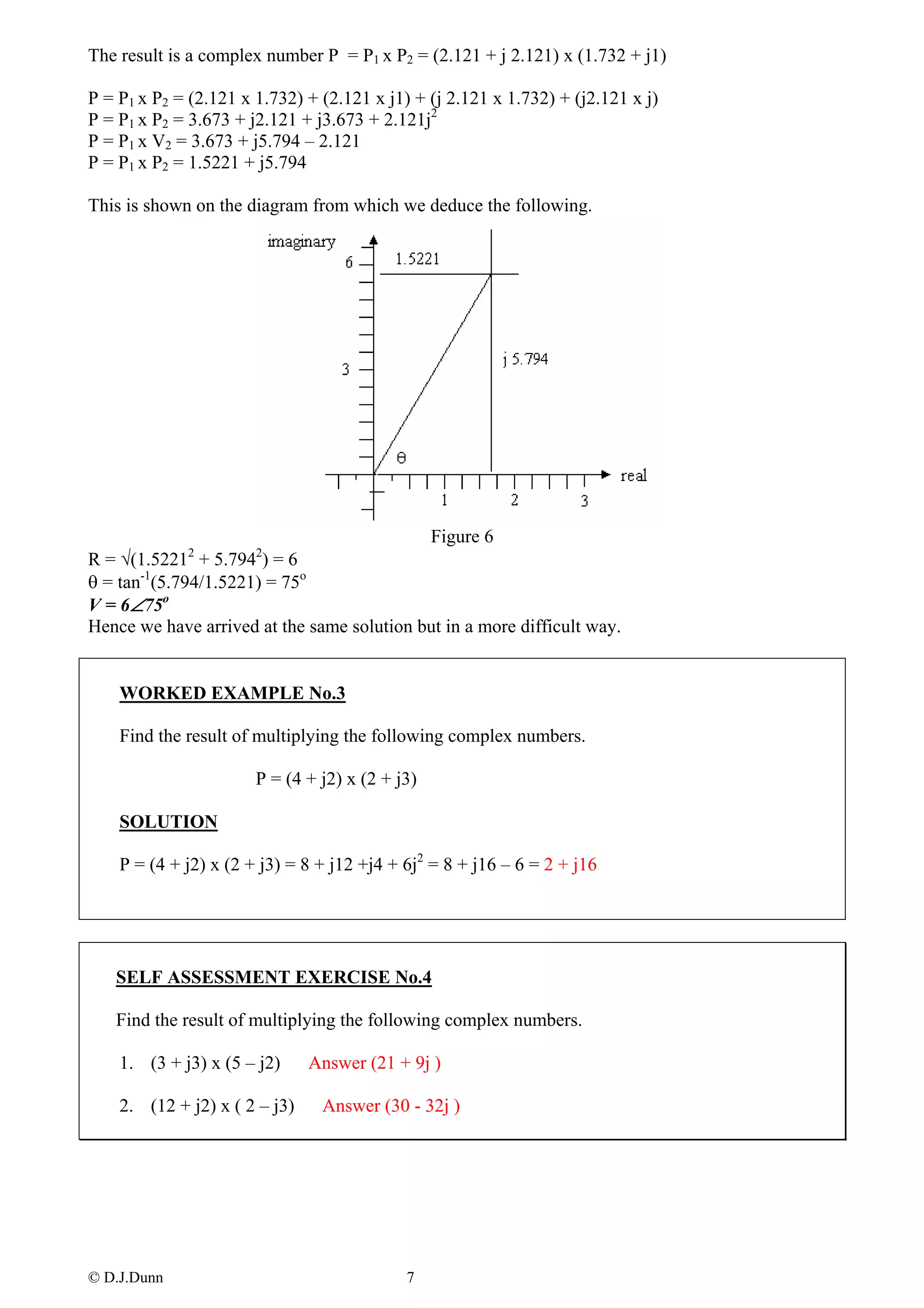
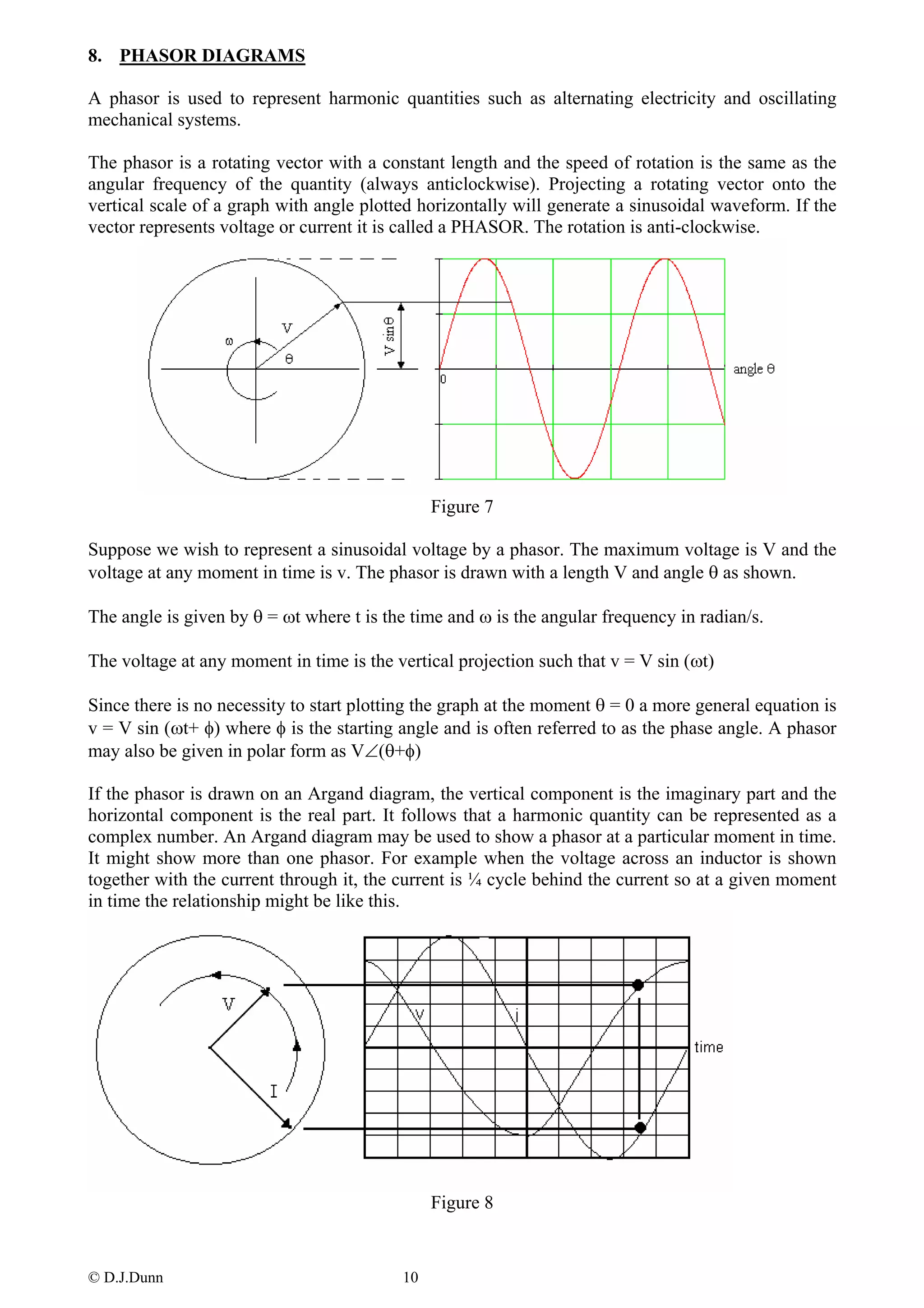
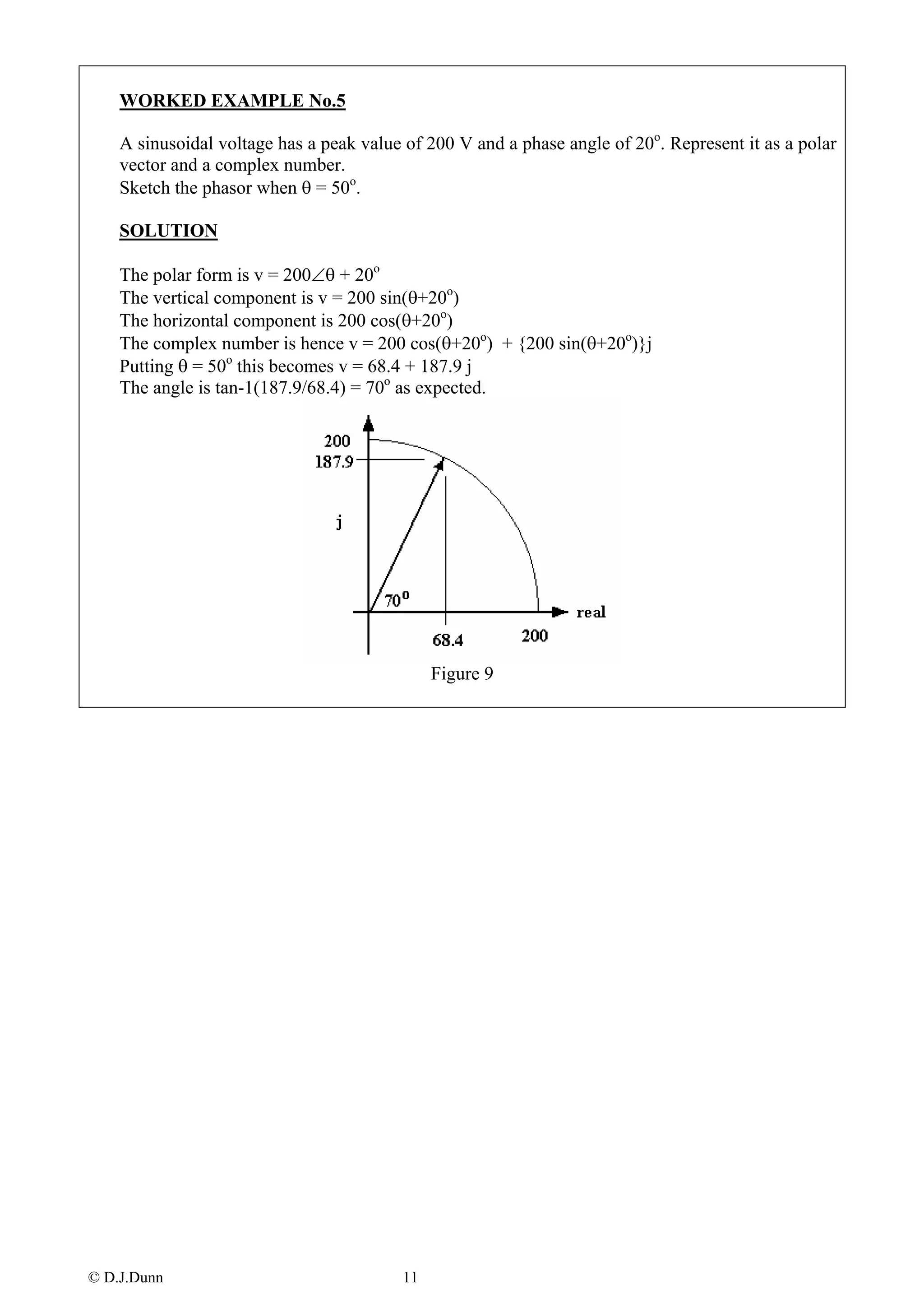
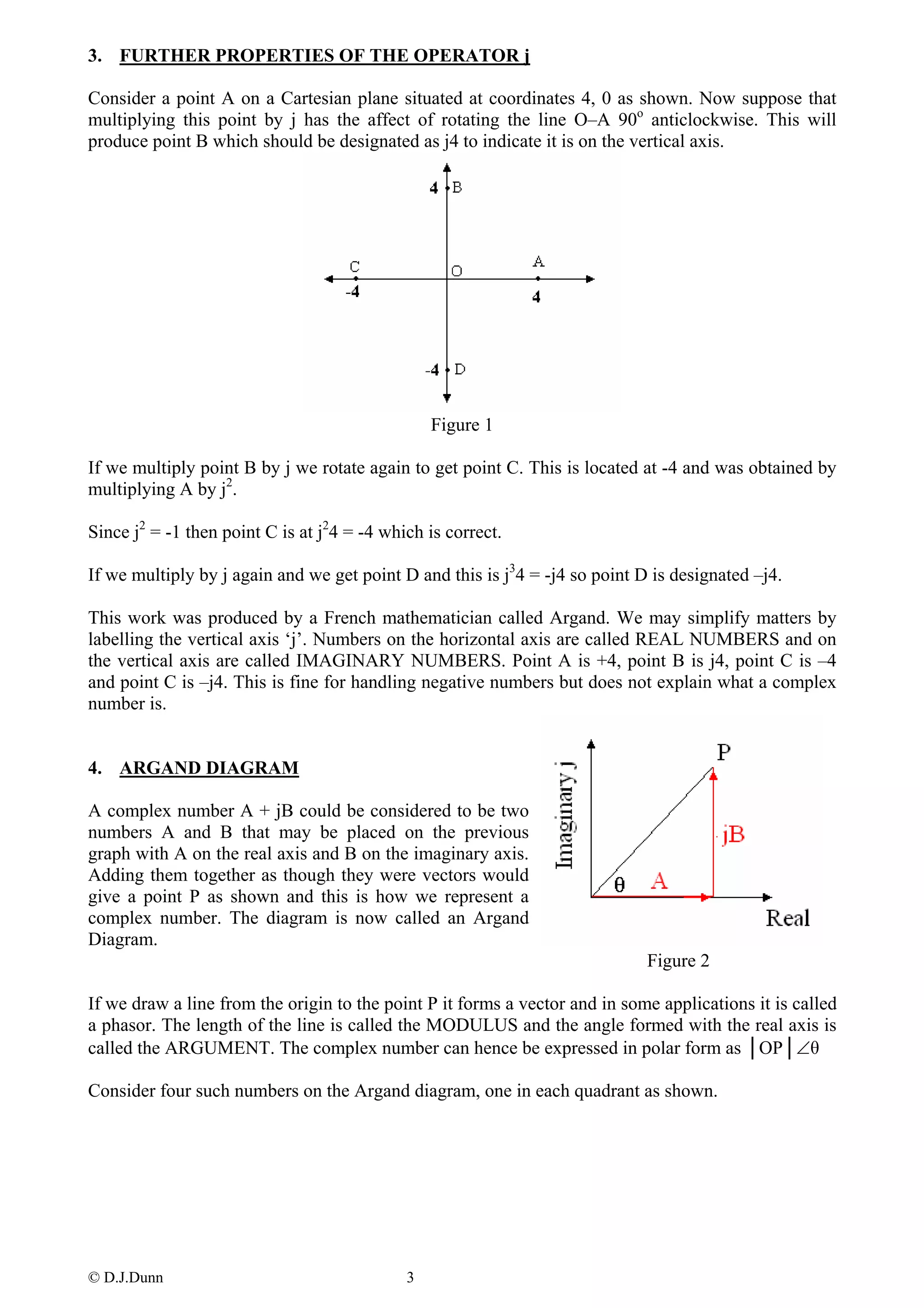
This document provides an overview of complex numbers for engineering students. It begins by explaining how complex numbers are used to represent the square root of negative numbers. It then defines complex numbers as having real and imaginary parts represented by the form a + bj. The rest of the document covers: - Representing complex numbers on an Argand diagram - Multiplying and dividing complex numbers using polar coordinates - Conjugate numbers and their use in multiplication and division - Phasor diagrams for representing alternating voltages and currents - Representing impedance as a complex number The overall aim is to explain key concepts involving complex numbers that are important for mechanical and electrical engineering applications.

1. MATHEMATICS FOR ENGINEERING
TUTORIAL 6 – COMPLEX NUMBERS
This tutorial is essential pre-requisite material for anyone studying
mechanical and electrical engineering. It follows on from tutorial 5 on
vectors. This tutorial uses the principle of learning by example. The
approach is practical rather than purely mathematical.
On completion of this tutorial you should be able to do the following.
• Explain and use complex numbers.
• Explain and use the Argand diagram.
• Explain and use vectors with polar co-ordinates.
• Multiply and divide complex numbers.
• Explain and use the conjugate number.
• Explain and use phasors and phasor diagrams.
• Explain the meaning of phase angle.
• Explain and use complex impedance.
It is presumed that students have already studied vectors, basic algebra and
trigonometry.
© D.J.Dunn 1

2. 1. ROOTS OF NEGATIVE NUMBERS
Ordinary numbers can be added, subtracted and multiplied and are good enough for every day use.
In engineering, we come across problems that can not be solved with ordinary numbers and one of
these problems is how to handle the square root of a negative number. You should already know
that 1 x 1 = 1 and that -1 x -1 = 1 so it follows that √1 is either 1 or -1. However there is no answer
to the question ‘what is the root of -1?’ There is no number that can be multiplied by its self to give
-1. To get around this problem in the first instance, we simply designate √-1 by the letter j and it
follows that j2 = -1 and j = √-1
Consider the equation x2 = -9. Using conventional numbers, there is no solution but using this new
idea, the solution becomes j3 since (j3)2 = j2 x 32 = -1 x 9 = -9.
2. COMPLEX NUMBER
Consider the number given as P = A + − B 2
If we use the j operator this becomes P = A + − 1 x B
Putting j = √-1we get P = A + jB and this is the form of a complex number.
WORKED EXAMPLE No.1
Find the solution of P = 4 + − 9 and express the answer as a complex number.
SOLUTION
P = 4 + − 9 = 4 + j3
SELF ASSESSMENT EXERCISE No.1
1. Write down the solution to the following.
x2 = -4 x=
2
x = -25 x=
x2 = -10 x=
(Answer j2, j5 and j√10)
2. Express the following as complex numbers.
P = 3 + − 16
P = 2 − − 81
P = −5 − − 12
Answers (3 + j4), (2 – j 9) and (-5 –j √12)
© D.J.Dunn 2

3. 3. FURTHER PROPERTIES OF THE OPERATOR j
Consider a point A on a Cartesian plane situated at coordinates 4, 0 as shown. Now suppose that
multiplying this point by j has the affect of rotating the line O–A 90o anticlockwise. This will
produce point B which should be designated as j4 to indicate it is on the vertical axis.
Figure 1
If we multiply point B by j we rotate again to get point C. This is located at -4 and was obtained by
multiplying A by j2.
Since j2 = -1 then point C is at j24 = -4 which is correct.
If we multiply by j again and we get point D and this is j34 = -j4 so point D is designated –j4.
This work was produced by a French mathematician called Argand. We may simplify matters by
labelling the vertical axis ‘j’. Numbers on the horizontal axis are called REAL NUMBERS and on
the vertical axis are called IMAGINARY NUMBERS. Point A is +4, point B is j4, point C is –4
and point C is –j4. This is fine for handling negative numbers but does not explain what a complex
number is.
4. ARGAND DIAGRAM
A complex number A + jB could be considered to be two
numbers A and B that may be placed on the previous
graph with A on the real axis and B on the imaginary axis.
Adding them together as though they were vectors would
give a point P as shown and this is how we represent a
complex number. The diagram is now called an Argand
Diagram.
Figure 2
If we draw a line from the origin to the point P it forms a vector and in some applications it is called
a phasor. The length of the line is called the MODULUS and the angle formed with the real axis is
called the ARGUMENT. The complex number can hence be expressed in polar form as │OP│∠θ
Consider four such numbers on the Argand diagram, one in each quadrant as shown.
© D.J.Dunn 3

4. Consider the vector labelled No.1. The horizontal component is 5 and the vertical component is 8 so
the vector may be written as P = 5 + j8.
The angle of the vector is tan-1 (8/5) = tan-1 (1.6) = 58o
Figure 3
SELF ASSESSMENT EXERCISE No. 2
1. Write down the other three vectors in the form A + jB and calculate their angles.
2 _______________________________________________
3 _______________________________________________
4 _______________________________________________
© D.J.Dunn 4

5. 5. MULTIPLYING COMPLEX NUMBERS
USING POLAR CO-ORDINATES
A complex number may be expressed in polar co-ordinates as follows. Let the Modulus be R and
the argument θ. Consider the two shown. We have R1 ∠θ1 and R2 ∠θ2
Figure 4
We should not confuse the multiplication of vectors (see dot and cross products in the vector
tutorials) with the multiplication of complex numbers.
The real and imaginary co-ordinates are
A1 = R1 cosθ1 B1 = R1 sinθ1
A2 = R2 cosθ2 B2 = R2 sinθ2
The complex number for each vector is:
P1 = R 1cosθ1 + jR 1sinθ1 = R 1{cosθ1 + jsinθ1}
P2 = R 2 cosθ 2 + jR 2 sinθ 2 = R 2 {cosθ 2 + jsinθ 2 }
Multiplying them together and treating j as √-1 we get the following.
P1 x P2 = R 1{cos θ1 + jsin θ1} x R 2 {cos θ 2 + jsin θ 2 }
P1 x P2 = R 1R 2 [cos θ1cos θ 2 + cos θ1 jsin θ 2 + jsin θ1cos θ 2 + jsin θ1 jsin θ 2 ]
[
P1 x P2 = R 1R 2 cos θ1cos θ 2 + j(cos θ1sin θ 2 + sin θ1cos θ 2 ) + j2 sin θ1sin θ 2 ]
P1 x P2 = R 1R 2 [cos θ1cos θ 2 − sin θ1sin θ 2 + j(cos θ1sin θ 2 + sin θ1cos θ 2 )]
P1 x P2 = R 1R 2 [cos(θ1 + θ 2 ) + jsin(θ 2 + θ 2 )]
This is a vector with a length R1R2 and angle θ1+θ2. The rule for multiplying is :
The Modulus is the product of the other Modulii and the argument is the sum of the angles. This
rule applies for any number of vectors multiplied together.
© D.J.Dunn 5

6. WORKED EXAMPLE No. 2
Find the result of (3 ∠45o) x (2 ∠30o)
SOLUTION
Modulus = 3 x 3 = 6
Argument is 45 + 30 = 75o
The result is hence 6∠75 o
SELF ASSESSMENT EXERCISE No.3
Find the vector that result for each below.
1. 5 ∠50o x 3 ∠70o
2. 7 ∠80o x 2 ∠30o
USING COMPLEX FORM
Consider the following problem. Multiply 3 ∠45o x 2 ∠30o. The result is 6∠75 o.
Figure 5
To do this as complex numbers is more difficult as we shall now see. In the form A + j B wehave
the following.
P1 has coordinates A1 = 3 cos 45 = 2.121 and B1 = 3 sin 45 = 2.121
P2 has coordinates A2 = 2 cos 30 = 1.732 and B2 = 2 sin 30 = 1.0
P1 = 2.121 + j 2.121 and P2 = 1.732 + j1
© D.J.Dunn 6

7. The result is a complex number P = P1 x P2 = (2.121 + j 2.121) x (1.732 + j1)
P = P1 x P2 = (2.121 x 1.732) + (2.121 x j1) + (j 2.121 x 1.732) + (j2.121 x j)
P = P1 x P2 = 3.673 + j2.121 + j3.673 + 2.121j2
P = P1 x V2 = 3.673 + j5.794 – 2.121
P = P1 x P2 = 1.5221 + j5.794
This is shown on the diagram from which we deduce the following.
Figure 6
R = √(1.52212 + 5.7942) = 6
θ = tan-1(5.794/1.5221) = 75o
V = 6∠75o
Hence we have arrived at the same solution but in a more difficult way.
WORKED EXAMPLE No.3
Find the result of multiplying the following complex numbers.
P = (4 + j2) x (2 + j3)
SOLUTION
P = (4 + j2) x (2 + j3) = 8 + j12 +j4 + 6j2 = 8 + j16 – 6 = 2 + j16
SELF ASSESSMENT EXERCISE No.4
Find the result of multiplying the following complex numbers.
1. (3 + j3) x (5 – j2) Answer (21 + 9j )
2. (12 + j2) x ( 2 – j3) Answer (30 - 32j )
© D.J.Dunn 7

8. 6. CONJUGATE NUMBERS
The conjugate of a complex number has the opposite sign for the j part.
The conjugate of A + jB is A – jB.
If a complex number is multiplied by its conjugate the result is a real number.
WORKED EXAMPLE No.4
Find the result of multiplying (2 + j3) by its conjugate.
SOLUTION
The conjugate is (2 - j3)
(2 + j3) x (2- j3) = 4 - 6j +6j -9j2 = 4 –(-9) = 13
SELF ASSESSMENT EXERCISE No.5
Find the result of multiplying the following by their conjugate.
1. (5 – j2) (Answer 29)
2. (-4 – j4) (Answer 32)
3. (7 + j6) (Answer 85)
© D.J.Dunn 8

9. 7. DIVISION OF COMPLEX NUMBERS
Suppose V = 8 + j8 and I = 4 - j8 and we wish to find V/I. (This is Ohms Law for complex
impedance). This is done by multiplying the top and bottom by the conjugate of the bottom number
as follows.
WORKED EXAMPLE No. 5
If A = 8 + j8 and B = 4 – j8 find the result of dividing A by B.
SOLUTION
V 8 + j8
=
I 4 − j8
V 8 + j8 4 + j8
= x
I 4 − j8 4 + j8
V 32 + j64 + j32 + j2 64
=
I 16 + j32 - j32 - j2 64
V 32 + j96 - 64 - 32 + j96 ⎛ 32 ⎞ ⎛ 96 ⎞
= = = - ⎜ ⎟ + j⎜ ⎟
I 16 + 64 90 ⎝ 90 ⎠ ⎝ 90 ⎠
SELF ASSESSMENT EXERCISE No.6
Find the following results.
V 1 + j2
1. = (Answer 0.7 – 0.1j)
I 1 + j3
V 5 − j2
2. = (Answer 0.1 + 1.2j)
I 2 − j4
x 1 − j9
3. = (Answer -1.3 - 0.6j)
y 2 + j6
© D.J.Dunn 9

10. 8. PHASOR DIAGRAMS
A phasor is used to represent harmonic quantities such as alternating electricity and oscillating
mechanical systems.
The phasor is a rotating vector with a constant length and the speed of rotation is the same as the
angular frequency of the quantity (always anticlockwise). Projecting a rotating vector onto the
vertical scale of a graph with angle plotted horizontally will generate a sinusoidal waveform. If the
vector represents voltage or current it is called a PHASOR. The rotation is anti-clockwise.
Figure 7
Suppose we wish to represent a sinusoidal voltage by a phasor. The maximum voltage is V and the
voltage at any moment in time is v. The phasor is drawn with a length V and angle θ as shown.
The angle is given by θ = ωt where t is the time and ω is the angular frequency in radian/s.
The voltage at any moment in time is the vertical projection such that v = V sin (ωt)
Since there is no necessity to start plotting the graph at the moment θ = 0 a more general equation is
v = V sin (ωt+ φ) where φ is the starting angle and is often referred to as the phase angle. A phasor
may also be given in polar form as V∠(θ+φ)
If the phasor is drawn on an Argand diagram, the vertical component is the imaginary part and the
horizontal component is the real part. It follows that a harmonic quantity can be represented as a
complex number. An Argand diagram may be used to show a phasor at a particular moment in time.
It might show more than one phasor. For example when the voltage across an inductor is shown
together with the current through it, the current is ¼ cycle behind the current so at a given moment
in time the relationship might be like this.
Figure 8
© D.J.Dunn 10

11. WORKED EXAMPLE No.5
A sinusoidal voltage has a peak value of 200 V and a phase angle of 20o. Represent it as a polar
vector and a complex number.
Sketch the phasor when θ = 50o.
SOLUTION
The polar form is v = 200∠θ + 20o
The vertical component is v = 200 sin(θ+20o)
The horizontal component is 200 cos(θ+20o)
The complex number is hence v = 200 cos(θ+20o) + {200 sin(θ+20o)}j
Putting θ = 50o this becomes v = 68.4 + 187.9 j
The angle is tan-1(187.9/68.4) = 70o as expected.
Figure 9
© D.J.Dunn 11

12. 9. REPRESENTING IMPEDANCE AS A COMPLEX NUMBER
When an electric circuit with alternating current contains resistance, inductance and capacitance, the
current and voltage will not vary in time together but one will lead the other. The above diagram
shows one example of this. The impedance of an electric circuit is defined as Z = V/I and in order to
divide V by I we must represent the phasor as a complex number. Suppose V = 8 + j8 and I = 4 -j8.
V 8 + j8
=
I 4 - j8
Multiply the top and bottom 4 + j8. This is called the conjugate number and it turns the bottom
The
line into a real number. This does not change the equality.
V 8 + j8 4 + j8 32 + j64 + j32 + j2 64 32 + j96 - 64 - 32 + j96 32 96
= x = = = =- + j
I 4 - j8 4 + j8 16 + j32 − j32 - j 64
2 16 + 64 80 80 80
The Impedance is Z = –(32/80) + j (96/80)
On an Argand diagram the voltage and current are like this.
Figure 10
Impedance is also a phasor and looks like this.
Figure 11
The real part is called the Resistance part (R) and the imaginary part is called the reactive part X.
⎛X⎞
It follows that. Z = X 2 + R 2 and φ = tan −1 ⎜ ⎟ and φ is called the phase angle.
⎝R⎠
It follows that complex impedance may be written in the form Z = R + jX and impedances may be
added or subtracted.
© D.J.Dunn 12

13. SELF ASSESSMENT EXERCISE No.7
1. An electric circuit has a complex impedance of Z = 300 + j40.
What is the resistance of the circuit and what is the reactance? (300 Ω and 40Ω)
What is the phase angle? (7.6o)
2. Two electric circuits are connected in series. The complex impedance of the first is Z = 50 +j3
and the second is Z = -20 + j2.
What is the combined impedance? (Add them). (30 +5j)
What is the resistance and reactance of the combined circuit? (30Ω and 5Ω)
What is the phase angle? (9.5o)
3. The current in an electric circuit is represented by I = 5 + j2 and the voltage is V = 100 +
j5.
Determine the impedance as a complex number. (17.6 + 6j)
Determine the resistance and reactance of the circuit. (17.6Ω and 6Ω)
Determine the phase angle. (18.8o)
© D.J.Dunn 13