The document discusses completing the square, which is a process for rewriting quadratic expressions in the form (x - h)2 + k. It provides examples of using completing the square to solve quadratic equations by making the left side a perfect square. The key steps are: 1) write the equation in the form ax2 + bx + c, 2) take half the coefficient of x and square it, 3) add this quantity to both sides, 4) group the left side as a squared binomial, 5) take the square root of both sides. Completing the square allows quadratic equations to be solved using the square root property and written in vertex form.

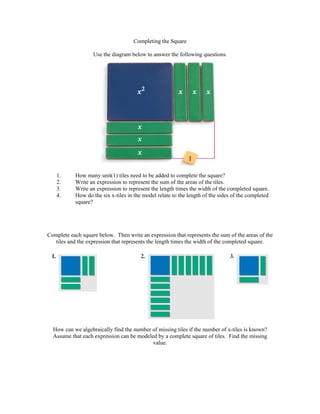
1. Completing the Square
Use the diagram below to answer the following questions.
1. How many unit(1) tiles need to be added to complete the square?
2. Write an expression to represent the sum of the areas of the tiles.
3. Write an expression to represent the length times the width of the completed square.
4. How do the six x-tiles in the model relate to the length of the sides of the completed
square?
Complete each square below. Then write an expression that represents the sum of the areas of the
tiles and the expression that represents the length times the width of the completed square.
How can we algebraically find the number of missing tiles if the number of x-tiles is known?
Assume that each expression can be modeled by a complete square of tiles. Find the missing
value.

2. How can we use the process of completing the square to solve quadratic functions?
The idea behind completing the square is to rewrite the equation in a form
that allows us to apply the square root property.
Solve by using square roots.
How could we solve the following equations by using the square roots property?
We can rewrite the left-hand side as a perfect square!
√(x+5)2 = ±√36
(x+5) = ±6
x + 5 = 6 or x + 5 = -6
x = 1 or -11
Solve using the square root property.
(x+2)(x+4) = 0
The following equation is NOT a perfect square! However, we can convert it into a perfect
square by completing the square.
If we refer back to the introduction problems where we had to figure out what number was
needed to complete the square, we found that we were to we can use this process to make perfect
squares in the form:

3. (a ± b)² = a² ± 2ab + b²
The first term and the last term are perfect squares and their signs are
positive. The middle term is twice the product of the square roots of these two
numbers. The sign of the middle term is plus if a sum has been squared; it is
minus if a difference has been squared.
To complete the square,
Step 1: Write the left side in the form x2 + bx.
Step 2: Take ½ of b, the coefficient of x.
Step 3: Square the result of Step 1.
b 
2
Step 4: Add the result of Step 2,   to each side of the equation.
 2
Step 5: Write the left side as a binomial squared.
Step 6: Use the Square Root Property to solve.
Let’s use the steps above to solve the previous example by completing the square.
Step 1: Write the left side in the form x2 + bx.
x2 + 6x = -8
Step 2: Take ½ of b, the coefficient of x.
½ (6) = 3
Step 3: Square the result of Step 1.
(3)2 = 9

4. b 
2
Step 4: Add the result of Step 2,   to each side of the equation.
2
x2 + 6x + 9 = -8 + 9
Step 5: Write the left side as a binomial squared.
(X + 3)2 = 1
Step 6: Use the Square Root Property to solve.
√(x+3)2 = ±√1
(x+3) = ±1
x + 3 = 1 or x + 3 = -1
x = -2 or -4
Example: x2 + 10x – 2 = 0
Step 1: x2 + 10x = 2
Write the left side in the form x2 + bx.
Step 2: ½ (10) = 5
Take ½ of b, the coefficient of x.
Step 3: (5)2 = 25
Square the result of Step 1.
Step 4: x2 + 10x + 25 = 2 + 25
b 
2
Add the result of Step 2,   to each side
2
of the equation.
Step 5: (x + 5)2 = 27
Write the left side as a binomial squared.
Step 6: √(x + 5)2 = ±√27
Use the Square Root Property to solve. x + 5 = ±3√3
x = -2 ±3√3

5. What happens if a ≠ 1?
You can only complete the square if the leading coefficient/quadratic term is 1. If the coefficient
is not 1, divide each term by the coefficient.
2x + 3x − 2 = 0
2
2
Now that the leading coefficient is 1, follow the steps from above.
3
x2 + x −1 = 0
2
Step 1: 3
Write the left side in the form x2 + bx. x2 + x = 1
2
Step 2: 13 3
Take ½ of b, the coefficient of x.  =
2 2 4
Step 3: 2
3 9
Square the result of Step 1.   =
 4  16
Step 4: 3 9 9
x2 + x + = 1 +
b 
2
2 16 16
Add the result of Step 2,   to each side
2
of the equation.
Step 5: 2
 3  25
Write the left side as a binomial squared. x+  =
 4  16
Step 6: 2
Use the Square Root Property to solve.  3 25
x+  = ±
 4 16
3 5
x+ = ±
4 4
3 5 −3 5
x= − + x= −
4 4 4 4
1
x = , −2
2

6. We can use completing the square to help use write our quadratic functions in vertex form, a(x –
h)2 + k.
Write the following function vertex form.
Use 0 = ax2 + bx + c as your reference equation, where y = 0.
Step 1: x2 + 6x = -2
Write the left side in the form x2 + bx.
Step 2: ½ (6) = 3
Take ½ of b, the coefficient of x.
Step 3: (3)2 = 9
Square the result of Step 1.
Step 4: x2 + 6x + 9 = -2 + 9
b 
2
Add the result of Step 2,   to each side
 2
of the equation.
Step 5: (x + 3)2 = 7
Write the left side as a binomial squared.
Step 6: (x + 3)2 – 7 = 0
Rewrite the equation so that it is in the form 0
= ax2 + bx + c
Step 7: Write your equation back in terms of (x + 3)2 – 7 = y
y.
Vertex is (-3, -7)