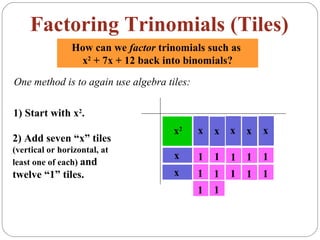
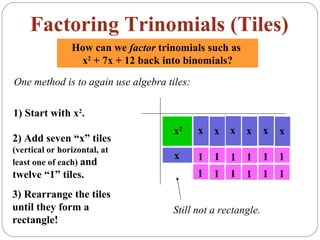
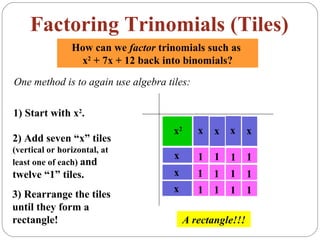
The document provides examples of factoring trinomials using algebra tiles and the factoring method. It begins by showing how to multiply binomials using FOIL and algebra tiles. It then demonstrates factoring trinomials like x^2 + 7x + 12 by arranging algebra tiles into a rectangle to reveal the factors (x + 4)(x + 3). Another method is shown that involves finding pairs of numbers whose product is the constant term and that add up to the coefficient of x. Examples are worked through to factor trinomials with and without leading coefficients.

1. Factoring

2. Factoring

3. Multiplying Binomials (FOIL)
Multiply. (x+3)(x+2)
Distribute. x•x+x•2+3•x+3•2
F O I L
= x2+ 2x + 3x + 6
= x2+ 5x + 6

4. Multiplying Binomials (Tiles)
Multiply. (x+3)(x+2)
Using Algebra Tiles, we have:
x + 3
x x2 x x x
+ = x2 + 5x + 6
x 1 1 1
2 x 1 1 1

5. Factoring Trinomials (Tiles)
How can we factor trinomials such as
x2 + 7x + 12 back into binomials?
One method is to again use algebra tiles:
1) Start with x2.
x2 x x x x x
2) Add seven “x” tiles
(vertical or horizontal, at
x 1 1 1 1 1
least one of each) and
twelve “1” tiles. x 1 1 1 1 1
1 1

6. Factoring Trinomials (Tiles)
How can we factor trinomials such as
x2 + 7x + 12 back into binomials?
One method is to again use algebra tiles:
1) Start with x2.
x2 x x x x x
2) Add seven “x” tiles
(vertical or horizontal, at
x 1 1 1 1 1
least one of each) and
twelve “1” tiles. x 1 1 1 1 1
3) Rearrange the tiles 1 1
until they form a
We need to change the “x” tiles so
rectangle!
the “1” tiles will fill in a rectangle.

7. Factoring Trinomials (Tiles)
How can we factor trinomials such as
x2 + 7x + 12 back into binomials?
One method is to again use algebra tiles:
1) Start with x2.
x2 x x x x x x
2) Add seven “x” tiles
(vertical or horizontal, at
x 1 1 1 1 1 1
least one of each) and
twelve “1” tiles. 1 1 1 1 1 1
3) Rearrange the tiles
until they form a Still not a rectangle.
rectangle!

8. Factoring Trinomials (Tiles)
How can we factor trinomials such as
x2 + 7x + 12 back into binomials?
One method is to again use algebra tiles:
1) Start with x2.
x2 x x x x
2) Add seven “x” tiles
(vertical or horizontal, at
x 1 1 1 1
least one of each) and
twelve “1” tiles. x 1 1 1 1
x 1 1 1 1
3) Rearrange the tiles
until they form a
rectangle! A rectangle!!!

9. Factoring Trinomials (Tiles)
How can we factor trinomials such as
x2 + 7x + 12 back into binomials?
One method is to again use algebra tiles:
4) Top factor: x + 4
The # of x2 tiles = x’s x x2 x x x x
The # of “x” and “1”
columns = constant. + x 1 1 1 1
3 x 1 1 1 1
5) Side factor:
The # of x2 tiles = x’s x 1 1 1 1
The # of “x” and “1”
rows = constant.
x2 + 7x + 12 = ( x + 4)( x + 3)

10. Factoring Trinomials (Method 2)
Again, we will factor trinomials such as
x2 + 7x + 12 back into binomials.
This method does not use tiles, instead we look
for the pattern of products and sums!
If the x2 term has no coefficient (other than 1)...
x2 + 7x + 12
Step 1: List all pairs of 12 = 1 • 12
numbers that multiply to
=2•6
equal the constant, 12.
=3•4

11. Factoring Trinomials (Method 2)
x2 + 7x + 12
Step 2: Choose the pair that 12 = 1 • 12
adds up to the middle
=2•6
coefficient.
=3•4
Step 3: Fill those numbers
into the blanks in the ( x + 3 )( x + 4 )
binomials:
x2 + 7x + 12 = ( x + 3)( x + 4)

12. Factoring Trinomials (Method 2)
Factor. x2 + 2x - 24
This time, the constant is negative!
Step 1: List all pairs of -24 = 1 • -24, -1 • 24
numbers that multiply to equal
the constant, -24. (To get -24, = 2 • -12, -2 • 12
one number must be positive and = 3 • -8, -3 • 8
one negative.)
= 4 • -6, - 4 • 6
Step 2: Which pair adds up to 2?
Step 3: Write the binomial x2 + 2x - 24 = ( x - 4)( x + 6)
factors.

13. Factoring Trinomials (Method 2*)
Factor. 3x2 + 14x + 8
This time, the x2 term DOES have a coefficient (other than 1)!
Step 1: Multiply 3 • 8 = 24 24 = 1 • 24
(the leading coefficient & constant).
= 2 • 12
Step 2: List all pairs of =3•8
numbers that multiply to equal
that product, 24. =4•6
Step 3: Which pair adds up to 14?

14. Factoring Trinomials (Method 2*)
Factor. 3x2 + 14x + 8
Step 4: Write temporary ( x + 2 )( x + 12 )
factors with the two numbers. 3 3
Step 5: Put the original 4
leading coefficient (3) under ( x + 2 )( x + 12 )
both numbers. 3 3
Step 6: Reduce the fractions, if ( x + 2 )( x + 4 )
possible. 3
Step 7: Move denominators in ( 3x + 2 )( x + 4 )
front of x.

15. Factoring Trinomials (Method 2*)
Factor. 3x2 + 14x + 8
You should always check the factors by distributing, especially
since this process has more than a couple of steps.
( 3x + 2 )( x + 4 ) = 3x • x + 3x • 4 + 2 • x + 2 • 4
= 3x2 + 14 x + 8 √
3x2 + 14x + 8 = (3x + 2)(x + 4)

16. Factoring Trinomials (Method 2*)
Factor 3x2 + 11x + 4
This time, the x2 term DOES have a coefficient (other than 1)!
Step 1: Multiply 3 • 4 = 12 12 = 1 • 12
(the leading coefficient & constant).
=2•6
Step 2: List all pairs of
numbers that multiply to equal =3•4
that product, 12.
Step 3: Which pair adds up to 11?
None of the pairs add up to 11, this trinomial
can’t be factored; it is PRIME.

17. Factor These Trinomials!
Factor each trinomial, if possible. The first four do NOT have
leading coefficients, the last two DO have leading coefficients.
Watch out for signs!!
1) t2 – 4t – 21
2) x2 + 12x + 32
3) x2 –10x + 24
4) x2 + 3x – 18
5) 2x2 + x – 21
6) 3x2 + 11x + 10

18. Solution #1: t2 – 4t – 21
1) Factors of -21: 1 • -21, -1 • 21
3 • -7, -3 • 7
2) Which pair adds to (- 4)?
3) Write the factors.
t2 – 4t – 21 = (t + 3)(t - 7)

19. Solution #2: x2 + 12x + 32
1) Factors of 32: 1 • 32
2 • 16
4•8
2) Which pair adds to 12 ?
3) Write the factors.
x2 + 12x + 32 = (x + 4)(x + 8)

20. Solution #3: x2 - 10x + 24
1) Factors of 32: 1 • 24 -1 • -24
2 • 12 -2 • -12
3•8 -3 • -8
4•6 -4 • -6
2) Which pair adds to -10 ? None of them adds to (-10). For
the numbers to multiply to +24
and add to -10, they must both be
negative!
3) Write the factors.
x2 - 10x + 24 = (x - 4)(x - 6)

21. Solution #4: x2 + 3x - 18
1) Factors of -18: 1 • -18, -1 • 18
2 • -9, -2 • 9
3 • -6, -3 • 6
2) Which pair adds to 3 ?
3) Write the factors.
x2 + 3x - 18 = (x - 3)(x + 18)

22. Solution #5: 2x2 + x - 21
1) Multiply 2 • (-21) = - 42; 1 • -42, -1 • 42
list factors of - 42. 2 • -21, -2 • 21
3 • -14, -3 • 14
2) Which pair adds to 1 ? 6 • -7, -6 • 7
3) Write the temporary factors. ( x - 6)( x + 7)
2 2
4) Put “2” underneath. 3
( x - 6)( x + 7)
5) Reduce (if possible).
2 2
6) Move denominator(s)in ( x - 3)( 2x + 7)
front of “x”.
2x2 + x - 21 = (x - 3)(2x + 7)

23. Solution #6: 3x2 + 11x + 10
1) Multiply 3 • 10 = 30; 1 • 30
list factors of 30. 2 • 15
3 • 10
2) Which pair adds to 11 ? 5•6
3) Write the temporary factors. ( x + 5)( x + 6)
3 3
4) Put “3” underneath. 2
( x + 5)( x + 6)
5) Reduce (if possible).
3 3
6) Move denominator(s)in ( 3x + 5)( x + 2)
front of “x”.
3x2 + 11x + 10 = (3x + 5)(x + 2)