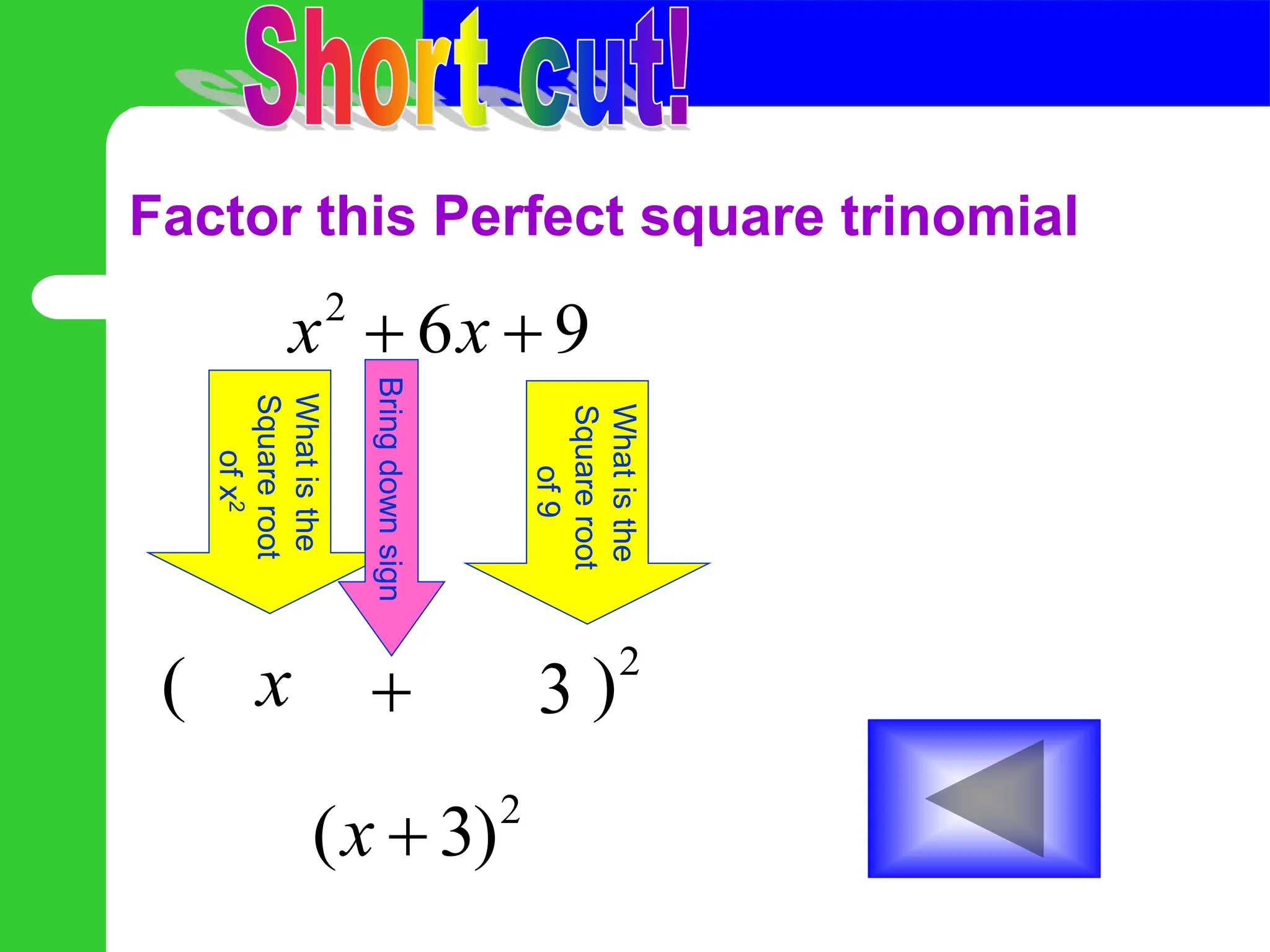
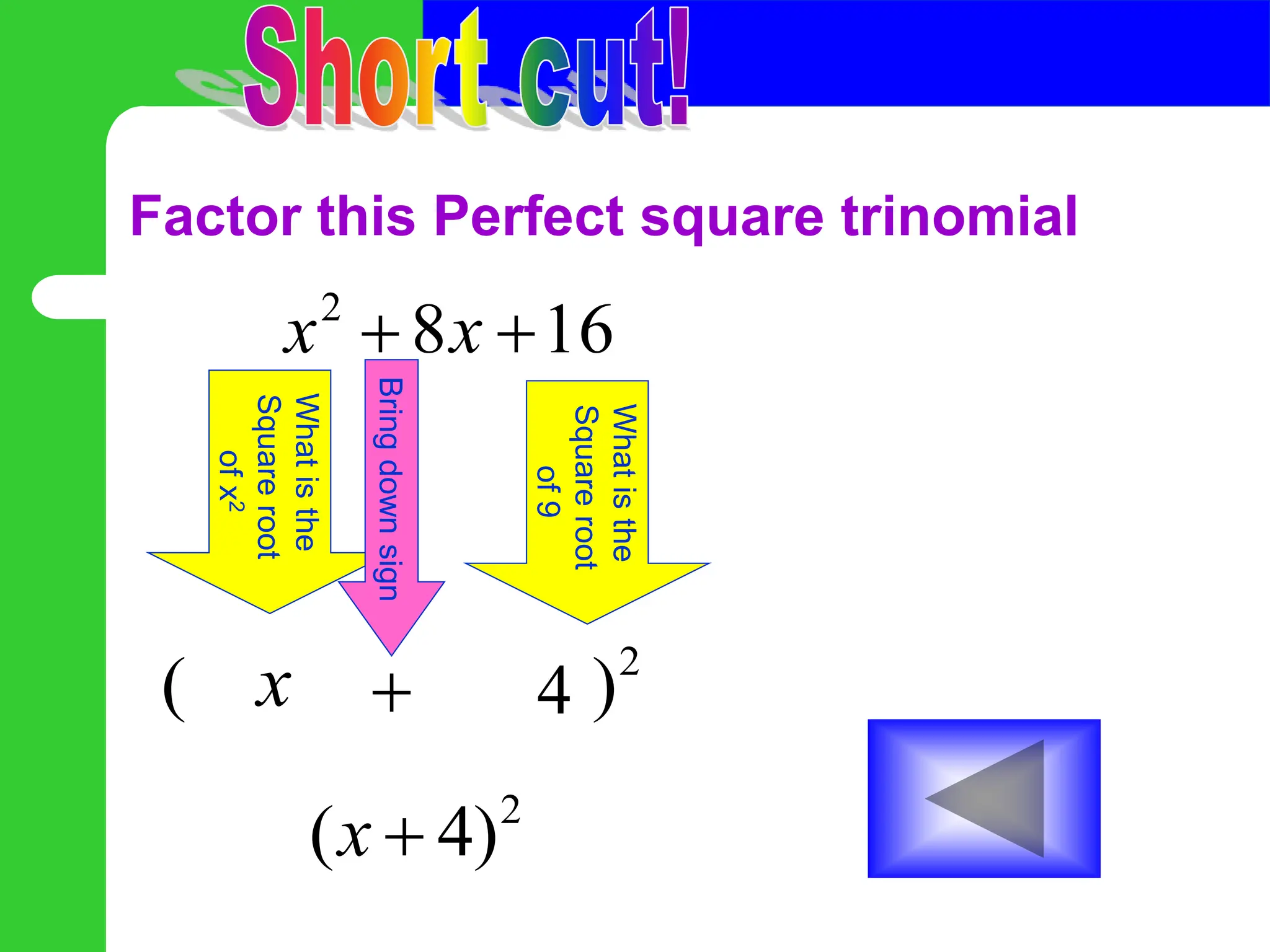
The document discusses the process of solving quadratic equations by completing the square. It begins by explaining that you must make the variable term a perfect square trinomial by adding a number to both sides of the equation. You calculate this number by taking half the coefficient of the linear term and squaring it. The steps are then demonstrated through examples: 1) move constants, 2) add a number to both sides to make the left side a perfect square, 3) factor the perfect square trinomial, 4) take the square root of both sides, and 5) solve for x.

1. Completing the Square
Solving Quadratics
By
Completing the Square
Part 2
Must be a
perfect
Square

2. 2
( 5) 64
x  
5 8
x   
When you take the
square root, You
MUST consider the
Positive and
Negative answers.
5 8
x    5 8
x   
5
 5

13
x  
5
 5

3
x  
Perfect
Square
On
One side
Take
Square Root
of
BOTH SIDES
2
( 5) 64
x  

3. Perfect
Square
On
One side
Take
Square Root
of
BOTH SIDES
But what happens if you DON’T
have a perfect square on one
side…….
You make it a Perfect Square
Use the relations on next slide…

4. 2
( 6)
x   (
2 )
 
To expand a perfect square binomial:
2
12 36
x x
  
6x 2
6
We can use these relations to find the missing term….To
make it a perfect square trinomial that can be factored into a
perfect square binomial.
2
_ _
12 _
x x
 
12 2
 6
 62
6 36

36
2
x

5.  Take ½ middle term
 Then square it
The resulting trinomial is called a perfect square
trinomial,
which can be factored into a perfect square
binomial.
2
_ _
18 _ _
x x
 
18 2
 9

2
(9) 81

81 2
( 9)
x 


6. 1. 2
12 0
x x
 
1. Make one side a
perfect square
2. Add a blank to
both sides
3. Divide “b” by 2
4. Square that
answer.
5. Add it to both
sides
6. Factor 1st side
7. Square root both
sides
8. Solve for x
2
0
x x
 
___
 ___
 12 2
 6

2
(6) 36

36 36
2
( 6)
x   36
2
( 6) 36
x  
6 6
x  
6 6
x   6 6
x  
6
 6

12
x  
6
 6

0
x 
12

7. Factor this Perfect square trinomial
2
12 36
x x
 
What
is
the
Square
root
of
x
2
2
( )
x
Bring
down
sign
 6
What
is
the
Square
root
of
36
2
( 6)
x 

8. 2. 2
8 0
x x
  
1. Move constant to
other side.
2. Add a blank to
both sides
3. Divide “b” by 2
4. Square that
answer.
5. Add it to both
sides
6. Factor 1st side
7. Square root both
sides
8. Solve for x
2
8
x x
  
___
 ___

6 2
 3

2
(3) 9

9 9
2
( 3)
x   1
2
( 3) 1
x  
3 1
x  
3 1
x   3 1
x  
3
 3

4
x  
3
 3

2
x  
6
6

9. Factor this Perfect square trinomial
2
6 9
x x
 
What
is
the
Square
root
of
x
2
2
( )
x
Bring
down
sign
 3
What
is
the
Square
root
of
9
2
( 3)
x 

10. 3. 2
8 84 0
x x
  
1. Move constant to
other side.
2. Add a blank to both
sides
3. Divide “b” by 2
4. Square that answer.
5. Add it to both sides
6. Factor 1st side
7. Square root both
sides
8. Solve for x
2
84
x x 
___
 ___

8 2
 4

2
(4) 16

16 16
2
( 4)
x   100
2
( 4) 100
x  
4 10
x  
4 10
x   4 10
x  
4
 4

14
x  
4
 4

6
x  
8


11. Factor this Perfect square trinomial
2
8 16
x x
 
What
is
the
Square
root
of
x
2
2
( )
x
Bring
down
sign
 4
What
is
the
Square
root
of
9
2
( 4)
x 

12. 4. 2
2 15 0
x x
  
1. Move constant to
other side.
2. Add a blank to both
sides
3. Divide “b” by 2
4. Square that answer.
5. Add it to both sides
6. Factor 1st side
7. Square root both
sides
8. Solve for x
2
15
x x 
___
 ___

2 2
 1

2
(1) 1

1 1
2
( 1)
x   16
2
( 1) 16
x  
1 4
x  
1 4
x   1 4
x  
1
 1

3
x  
1
 1

5
x  
2


13. Factor this Perfect square trinomial
2
2 1
x x
 
What
is
the
Square
root
of
x
2
2
( )
x
Bring
down
sign
 1
What
is
the
Square
root
of
9
2
( 1)
x 

14. Steps to solve Quadratics by
completing the square:
 Move the constant to side by itself.
 Make the side (w/variables) a perfect square by
adding a certain number to both sides.
 To calculate this number
– Divide “b” (middle term) by 2
– Then square that answer
 Take the square root of both sides of eq
 Then solve for x

15. In a perfect square, there is a
relationship between the coefficient of
the middle term and the constant term.
2
( 7)
x  
7 
1
(14)
2
2
7  49
2
14 49
x x
 
7

16. Warm – Up #11


17. Solving Quadratic
Equations by
Completing the
Square

18. EQ: How do you solve quadratics
by completing the square?
 MCC9-12.A.REI.4b Solve quadratic
equations by inspection, taking square roots,
completing the square, the quadratic formula
and factoring, as appropriate to the initial
form of the equation. Recognize when the
quadratic formula gives complex solutions
and write them as a ± bi for real numbers a
and b.

19. Perfect Square Trinomials
 Examples
 x2 + 6x + 9
 x2 - 10x + 25
 x2 + 12x + 36

20. Creating a Perfect
Square Trinomial
 In the following perfect square
trinomial, the constant term is
missing.
X2 + 14x + ____
 Find the constant term by
squaring half the coefficient of
the linear term.
 (14/2)2
X2 + 14x + 49

21. Perfect Square Trinomials
 Create perfect
square trinomials.
 x2 + 20x + ___
 x2 - 4x + ___
 x2 + 5x + ___
100
4
25/4

22. Solving Quadratic Equations by
Completing the Square
Solve the following
equation by
completing the
square:
Step 1: Move
quadratic term, and
linear term to left
side of the
equation
2
8 20 0
x x
  
2
8 20
x x
 

23. Solving Quadratic Equations by
Completing the Square
Step 2: Find the term
that completes the square
on the left side of the
equation. Add that term
to both sides.
2
8 =20 +
x x
 
2
1
( ) 4 then square it, 4 16
2
8
  
2
8 20
16 16
x x
   

24. Solving Quadratic Equations
by Completing the Square
Step 3: Factor
the perfect
square trinomial
on the left side
of the equation.
Simplify the
right side of the
equation.
2
8 20
16 16
x x
   
2
( 4)( 4) 36
( 4) 36
x x
x
  
 

25. Solving Quadratic Equations by
Completing the Square
Step 4:
Take the
square
root of
each side
2
( 4) 36
x  
( 4) 6
x   

26. Solving Quadratic Equations by
Completing the Square
Step 5: Set
up the two
possibilities
and solve
4 6
4 6 and 4 6
10 and 2
x=
x
x x
x
  

 
    

27. Completing the Square-Example
#2
Solve the following
equation by completing
the square:
Step 1: Move quadratic
term, and linear term to
left side of the equation,
the constant to the right
side of the equation.
2
2 7 12 0
x x
  
2
2 7 12
x x
  

28. Solving Quadratic Equations
by Completing the Square
Step 2: Find the term
that completes the square
on the left side of the
equation. Add that term
to both sides.
The quadratic coefficient
must be equal to 1 before
you complete the square, so
you must divide all terms
by the quadratic
coefficient first.
2
2
2
2 7
2
2 2 2
7 12
7
2
=-12 +
6
x x
x x
x
x
 
 
 
  
  
2
1 7 7 49
( ) then square it,
2 6
2 4 4 1
7  
  
 
 
2 49 49
16 1
7
6
2 6
x x
    

29. Solving Quadratic Equations
by Completing the Square
Step 3: Factor
the perfect
square trinomial
on the left side
of the equation.
Simplify the
right side of the
equation.
2
2
2
7
6
2
7 96 49
4 16 16
7 47
4
49 49
16 1
16
6
x x
x
x
    
 
   
 
 
 
  
 
 

30. Solving Quadratic Equations by
Completing the Square
Step 4:
Take the
square
root of
each side
2
7 47
( )
4 16
x

 
7 47
( )
4 4
7 47
4 4
7 47
4
x
i
x
i
x

  
 



31. Solving Quadratic Equations by
Completing the Square
2
2
2
2
2
1. 2 63 0
2. 8 84 0
3. 5 24 0
4. 7 13 0
5. 3 5 6 0
x x
x x
x x
x x
x x
  
  
  
  
  
Try the following examples. Do your work on your paper and then check
your answers.
 
 
1. 9,7
2.(6, 14)
3. 3,8
7 3
4.
2
5 47
5.
6
i
i



 
 
 
 
 
 
 
 
 
 