Recommended
PPT
PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PDF
プログラミングコンテストでのデータ構造 2 ~動的木編~
PDF
PDF
RSA暗号運用でやってはいけない n のこと #ssmjp
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
二部グラフの最小点被覆と最大安定集合と最小辺被覆の求め方
PDF
プログラミングコンテストでのデータ構造 2 ~平衡二分探索木編~
PDF
PDF
PDF
PPTX
PDF
PDF
競技プログラミングにおけるコードの書き方とその利便性
PDF
PDF
More Related Content
PPT
PDF
PDF
PDF
PDF
PDF
PPTX
PDF
What's hot
PDF
プログラミングコンテストでのデータ構造 2 ~動的木編~
PDF
PDF
RSA暗号運用でやってはいけない n のこと #ssmjp
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
二部グラフの最小点被覆と最大安定集合と最小辺被覆の求め方
PDF
プログラミングコンテストでのデータ構造 2 ~平衡二分探索木編~
PDF
PDF
PDF
PPTX
PDF
PDF
競技プログラミングにおけるコードの書き方とその利便性
Viewers also liked
PDF
PDF
PDF
浮動小数点(IEEE754)を圧縮したい@dsirnlp#4
PDF
PDF
LLVMで遊ぶ(整数圧縮とか、x86向けの自動ベクトル化とか)
PDF
汎用性と高速性を目指したペアリング暗号ライブラリ mcl
PDF
PDF
JIT Code Profiling with VTune
PDF
PDF
MS Officeファイル暗号化のマスター鍵を利用したバックドアとその対策
PDF
Treasure Dataを支える技術 - MessagePack編
PDF
PDF
PDF
PDF
PDF
PDF
Cybozu Tech Conference 2016 バグの調べ方
PDF
爆速クエリエンジン”Presto”を使いたくなる話
PPTX
PDF
「HOME'Sデータセット」を活用した不動産物件画像への深層学習の適用の取り組み
Similar to 条件分岐とcmovとmaxps
PDF
PDF
PDF
PDF
PDF
統計解析言語Rにおける大規模データ管理のためのboost.interprocessの活用
PDF
PDF
PPTX
PDF
C++0x in programming competition
PDF
PPTX
PDF
PDF
第11回 配信講義 計算科学技術特論B(2022)
PDF
PDF
x64 のスカラー,SIMD 演算性能を測ってみた v0.1 @ C++ MIX #10
PDF
x64 のスカラー,SIMD 演算性能を測ってみた @ C++ MIX #10
PDF
PDF
機械学習とこれを支える並列計算 : 並列計算の現状と産業応用について
PDF
PDF
Sec15 dynamic programming
More from MITSUNARI Shigeo
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Intel AVX-512/富岳SVE用SIMDコード生成ライブラリsimdgen
PDF
PDF
PDF
PDF
PDF
PDF
深層学習フレームワークにおけるIntel CPU/富岳向け最適化法
PDF
PDF
PDF
Lifted-ElGamal暗号を用いた任意関数演算の二者間秘密計算プロトコルのmaliciousモデルにおける効率化
PDF
PDF
PDF
条件分岐とcmovとmaxps 1. 2. 3. 4. 5. 6. 7. 8. 古典的なテクニック
範囲チェック
unsigned int a, b, x;
if (a <= x && x <= b) { ... }
分岐が2回
cmp x, a
jb #elese
cmp x, b
ja #else
...
次のようにすると分岐は1回
if ((x – a) <= (b – a)) { ... }
後半の文字列で再度登場
8 /24
9. 10. 11. jmp命令を使う
jmp-cmov.cpp抜粋
L(".lp");
mov(t, ptr [x + n * 4]); // x[i]を読んで
cmp(t, ptr [y + n * 4]); // y[i]と比較して
jle(".skip"); // x[i] <= y[i]ならskip
add(a, 1); // count++
L(".skip");
add(n, 1);
jne(".lp");
1ループあたり10~12clk
重たい
11 /24
12. 13. adc命令を使う
L(".lp");
mov(edx, ptr [y + n * 4]); // y[i]を読んで
cmp(edx, ptr [x + n * 4]); // x[i]と比較して
adc(eax, 0); // ???
add(n, 1);
jne(".lp");
adcはcarryつきadd命令
cmpしたときにcarry = y[i] < x[i] ? 1 : 0
eax = eax + 0 + carry
= eax + (x[i] > y[i] ? 1 : 0);
(注意)符号無しの計算になるのでx[i], y[i] >= 0を仮定
13 /24
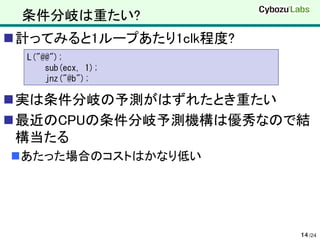
14. 15. 条件分岐は重たい?
与えられた配列の最大値の取得(cmov vs. jge)
int getMax_C(const int *x, size_t n)
{
int max = x[0];
for (size_t i = 1; i < n; i++) {
if (x[i] > max) max = x[i];
}
return max;
}
// a = max // a = max
cmp(a, ptr [x + n * 4]); cmp(a, ptr [x + n * 4]);
jge(".skip");
// if (a > x[i]) a = x[i] mov(a, ptr [x + n * 4]);
cmovl(a, ptr [x + n * 4]); L(".skip");
15 /24
16. 17. もう少しベンチマーク
大抵はjmpが速そうだ(@i7)
ランダム 最初が一番大きい 単調増加 時々増加
jmp 1.859 1.823 1.836 3.637
cmov 2.741 2.718 2.747 2.751
ちなみに最初のcountMaxのベンチマーク
x[i] > y[i]となる割合
一番予測できないときjmpの数値が非常に悪い
rate 0.00 0.25 0.50 0.75 1.00
jmp 1.863 7.827 12.747 9.276 1.854
setg 2.054 2.043 2.052 2.026 2.054
adc 1.842 1.838 1.849 1.828 1.822
17 /24
18. 19. SIMDを使ってみる
maxps = max(x[i], y[i]) for i = 0..3 を求める
// xm0 = [x[3]:x[2]:x[1]:x[0]
L("@@");
maxps(xm0, ptr [x + n * 4]); // update xm0
add(n, 4);
jnz("@b");
// ループが終わったらxm0のうちの一番大きいものを求める
i7 ランダム 最初が一番大きい 単調増加 時々増加
jmp 1.859 1.823 1.836 3.637
cmov 2.741 2.718 2.747 2.751
maxps 0.686 0.689 0.677 0.687
SIMD凄い!
19 /24
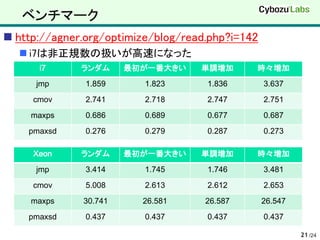
20. 21. ベンチマーク
http://agner.org/optimize/blog/read.php?i=142
i7は非正規数の扱いが高速になった
i7 ランダム 最初が一番大きい 単調増加 時々増加
jmp 1.859 1.823 1.836 3.637
cmov 2.741 2.718 2.747 2.751
maxps 0.686 0.689 0.677 0.687
pmaxsd 0.276 0.279 0.287 0.273
Xeon ランダム 最初が一番大きい 単調増加 時々増加
jmp 3.414 1.745 1.746 3.481
cmov 5.008 2.613 2.612 2.653
maxps 30.741 26.581 26.587 26.547
pmaxsd 0.437 0.437 0.437 0.437
21 /24
22. 23. 24.


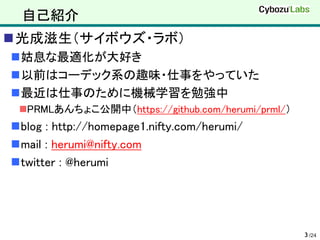






![例題1. countMax
次の関数を最適化せよ
分岐命令をcmovやsetgに置き換えよ
(注意)x[i], y[i] >= 0を仮定する
size_t countMax_C(const int *x, const int *y, size_t n)
{
size_t count = 0;
for (size_t i = 0; i < n; i++) {
if (x[i] > y[i]) count++;
}
return count;
}
10 /24](https://image.slidesharecdn.com/x86opti1-110806163532-phpapp01/85/cmov-maxps-10-320.jpg)
![jmp命令を使う
jmp-cmov.cpp抜粋
L(".lp");
mov(t, ptr [x + n * 4]); // x[i]を読んで
cmp(t, ptr [y + n * 4]); // y[i]と比較して
jle(".skip"); // x[i] <= y[i]ならskip
add(a, 1); // count++
L(".skip");
add(n, 1);
jne(".lp");
1ループあたり10~12clk
重たい
11 /24](https://image.slidesharecdn.com/x86opti1-110806163532-phpapp01/85/cmov-maxps-11-320.jpg)
![setg命令を使う
setXXは条件が満たされたときに8bitレジスタを1に
設定する(外れたら0)命令
8bitなのが結構使いにくい
jmp-cmov.cpp抜粋
L(".lp");
mov(edx, ptr [x + n * 4]); // x[i]を読んで
cmp(edx, ptr [y + n * 4]); // y[i]と比較して
setg(dl); // dl = x[i] > y[i] ? 1 : 0
movzx(edx, dl); // 上位24bitを0クリア
add(eax, edx); // countに加算
add(n, 1);
jne(".lp");
1ループあたり2~2.5clk!
12 /24](https://image.slidesharecdn.com/x86opti1-110806163532-phpapp01/85/cmov-maxps-12-320.jpg)
![adc命令を使う
L(".lp");
mov(edx, ptr [y + n * 4]); // y[i]を読んで
cmp(edx, ptr [x + n * 4]); // x[i]と比較して
adc(eax, 0); // ???
add(n, 1);
jne(".lp");
adcはcarryつきadd命令
cmpしたときにcarry = y[i] < x[i] ? 1 : 0
eax = eax + 0 + carry
= eax + (x[i] > y[i] ? 1 : 0);
(注意)符号無しの計算になるのでx[i], y[i] >= 0を仮定
13 /24](https://image.slidesharecdn.com/x86opti1-110806163532-phpapp01/85/cmov-maxps-13-320.jpg)
![条件分岐は重たい?
与えられた配列の最大値の取得(cmov vs. jge)
int getMax_C(const int *x, size_t n)
{
int max = x[0];
for (size_t i = 1; i < n; i++) {
if (x[i] > max) max = x[i];
}
return max;
}
// a = max // a = max
cmp(a, ptr [x + n * 4]); cmp(a, ptr [x + n * 4]);
jge(".skip");
// if (a > x[i]) a = x[i] mov(a, ptr [x + n * 4]);
cmovl(a, ptr [x + n * 4]); L(".skip");
15 /24](https://image.slidesharecdn.com/x86opti1-110806163532-phpapp01/85/cmov-maxps-15-320.jpg)

![もう少しベンチマーク
大抵はjmpが速そうだ(@i7)
ランダム 最初が一番大きい 単調増加 時々増加
jmp 1.859 1.823 1.836 3.637
cmov 2.741 2.718 2.747 2.751
ちなみに最初のcountMaxのベンチマーク
x[i] > y[i]となる割合
一番予測できないときjmpの数値が非常に悪い
rate 0.00 0.25 0.50 0.75 1.00
jmp 1.863 7.827 12.747 9.276 1.854
setg 2.054 2.043 2.052 2.026 2.054
adc 1.842 1.838 1.849 1.828 1.822
17 /24](https://image.slidesharecdn.com/x86opti1-110806163532-phpapp01/85/cmov-maxps-17-320.jpg)

![SIMDを使ってみる
maxps = max(x[i], y[i]) for i = 0..3 を求める
// xm0 = [x[3]:x[2]:x[1]:x[0]
L("@@");
maxps(xm0, ptr [x + n * 4]); // update xm0
add(n, 4);
jnz("@b");
// ループが終わったらxm0のうちの一番大きいものを求める
i7 ランダム 最初が一番大きい 単調増加 時々増加
jmp 1.859 1.823 1.836 3.637
cmov 2.741 2.718 2.747 2.751
maxps 0.686 0.689 0.677 0.687
SIMD凄い!
19 /24](https://image.slidesharecdn.com/x86opti1-110806163532-phpapp01/85/cmov-maxps-19-320.jpg)
![実はちょっとした落とし穴
Xeon, Core2Duoなどのプロセッサでは劇遅
Xeonだと30clk以上!
PentiumDだと速かったりする
maxpsは浮動小数点数(float)に対する命令
普通の整数値はfloatとしてみると非正規化数になっちゃ
うことも多い
ペナルティを食らう
float x[N]に対する先程の命令ではXeonだと0.648clk
PentiumDの頃は型にうるさく無かった?
整数に対するmax命令はpmaxsd
SSE4.1にしか無いがmaxpsよりは速い
20 /24](https://image.slidesharecdn.com/x86opti1-110806163532-phpapp01/85/cmov-maxps-20-320.jpg)