The document discusses optimization techniques for deep learning frameworks on Intel CPUs and Fugaku aimed architectures. It introduces oneDNN, a performance library for deep learning operations on Intel CPUs. It discusses issues with C++ implementation, and how just-in-time assembly generation using Xbyak can address these issues by generating optimal code depending on parameters. It also introduces Xbyak_aarch64 for generating optimized code for Fugaku's Scalable Vector Extension instructions.

1. 深層学習フレームワークにおける
Intel CPU/富岳向け最適化法
2021/6/24
計算科学技術特論A（2021）第11回
光成滋生

2. • サイボウズ・ラボで暗号とセキュリティに関するR&D
• 先月の早稲田大学での講演資料
• 私とOSSの25年 https://www.slideshare.net/herumi/oss25
• JITアセンブラXbyakの開発
• Intel oneDNN
• 富岳のDNN
• 富岳用のJITアセンブラXbyak_aarch64
• ペアリング暗号・BLS署名ライブラリの開発
• https://github.com/herumi/mcl
• Ethereumなどのブロックチェーン系プロジェクト
自己紹介
2 / 69

3. • 目的
• 機械学習特有の最適化の事情と
AVX-512/SVEのSIMDプログラミングの基本を学ぶ
• oneDNN
• C++で実装するときの懸念点
• JITアセンブラ
• SIMD
• AVX-512
• AVX-512のDNN向け命令紹介
• logの実装例
• SVEによるlogの実装例
• A64FXのレジスタの依存関係に関する細かい話
• 時間があればIntel AMXの紹介
目次
3 / 69

4. oneDNN

5. • TensorFlowやPyTorchなど
• 機械学習、深層学習の著名なフレームワーク
• そのフレームワークの中でGPUならcuDNN,
Intel CPUならoneDNNが利用されている
• oneDNN
• DNN向けのパフォーマンスライブラリ
• Intel CPU以外のCPU(AArch64やs390xなど), GPUもサポート
• https://jp.xlsoft.com/documents/intel/oneapi/download/oneapi-specification.pdf
oneDNN
TensorFlow
PyTorch
cuDNN NVIDIA GPU
oneDNN x64, A64FX, PPC64,
NVIDIA GPU, s390x
5 / 69

6. • プリミティブ
• CNN（畳み込み, 内積, ... ）
• 正規化（バッチ, レイヤー, ...）
• 要素ごとの操作（活性化関数 : ReLU, tanh, ...）
• データレイアウト間の並び替え操作
• uint32_t, float, double, uint8_t, bloat16など
• 基本的に
• ひたすら多次元配列の積和演算
• 𝑑𝑠𝑡 𝑛, 𝑐, ℎ, 𝑤 = 𝑏𝑖𝑎𝑠 𝑐 +
σ𝑖𝑐
σ𝑖ℎ
σ𝑖𝑤
𝑠𝑟𝑐 𝑛, 𝑖𝑐, ℎ′, 𝑤′ 𝑤( 𝑐, 𝑖𝑐, 𝑖ℎ, 𝑖𝑤)
where ℎ′
= 𝑓𝑢𝑛𝑐 ℎ, 𝑖ℎ , 𝑤′
= 𝑓𝑢𝑛𝑐(𝑤, 𝑖𝑤)
• 要素ごとに活性化関数の適用
DNNの主な計算
6 / 69

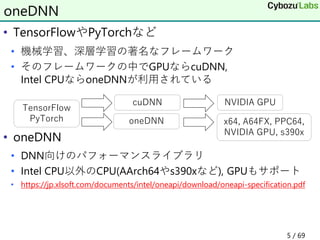
7. • 配列の和
• 素朴なasmコード
単純ループ
float sum(const float *x, size_t n) {
float r = 0;
for (size_t i = 0; i < n; i++) r += x[i];
return r;
}
xorps r, r // r = 0
test n, n
jz .exit
xor i, i // i = 0
.lp:
addss r, [x + i * 4] // r += x[i]
add i, 1 // i++
cmp i, n // if (i < n)
jne .lp // goto lp
.exit:
7 / 69

8. • ループアンロールすると77行（clang -Ofast）
• 32個単位で処理するループと端数処理と
• n = 2や3と分かっているならとても簡単なのに
ループアンロールと冗長なコード
...
movups xmm2, [rdi+rdx*4]
addps xmm2,xmm0
movups xmm0, [rdi+rdx*4+0x10]
addps xmm0,xmm1
movups xmm1, [rdi+rdx*4+0x20]
movups xmm3, [rdi+rdx*4+0x30]
movups xmm4, [rdi+rdx*4+0x40]
addps xmm4,xmm1
addps xmm4,xmm2
movups xmm2, [rdi+rdx*4+0x50]
addps xmm2,xmm3
addps xmm2,xmm0
movups xmm0, [rdi+rdx*4+0x60]
addps xmm0,xmm4
movups xmm1, [rdi+rdx*4+0x70]
addps xmm1,xmm2
add rdx,0x20
add rcx,0x4
...
// n = 2
movss r, [x + 0]
addss r, [x + 4]
ret
// n = 3
movss r, [x + 0]
addss r, [x + 4]
addss r, [x + 8]
ret
8 / 69

9. • iN x jN x kN個からなる3次元配列の(i, j, k)番目は
iN*jN*k+iN*j+i番目のアドレス
• アドレス計算にはコストがかかる
• addr = (jN * k + j) * iN + i
多次元配列の添え字の計算
iN
jN
kN
i
j
k
mov rdx, jN
imul rdx, k // jN * k
add rdx, j // jN * k + j
imul rdx, iN // (jN * k + j) * iN
add rdx, i // (jN * k + j) * iN + i
movss r, [x + rdx * 4]
9 / 69

10. • 多数のループの畳み込み
• ループの順序を入れ換えても計算結果は同じ
• キャッシュの影響で実行時間は異なる
• パラメータやCPUによって最適な順序が異なる
• 事前に多数のパターンを用意しておくのは組み合わせが大変
多重ループの順序
for oh
for ow
for oc
for ic
for kh
for kw
dst[oc, ow, oh] += ker[oc, ic, kw, kh] * src[ic, ow+kw, oh+kh]
10 / 69

11. • 畳み込み（conv）等の後に要素ごとの処理eltwise
• tanh, ReLU, clip, log, logisticなど様々な処理
• 配列が大きいとCPUキャッシュが無駄に
• 配列が小さいとオーバーヘッドが大きい
• SIMD処理はある程度のループが必要
• 関数プロローグ・エピローグ処理が相対的に重くなる
活性化関数の処理
conv eltwise ...
conv
eltwise
conv
elt
conv
elt
conv
elt
conv
elt
11 / 69

12. • 懸念点
• DNNは与えるパラメータの種類が非常に多い
• が、計算が始まるとそれらのパラメータは固定なものが多い
• 基本は積和演算だがループが深い
• ユーザが決める関数の種類も多い
• 演算回数が多いので少しでも速くしたい
• C++ではコンパイル時に決められないパターンが多い
• 実行時に決めたい
• Intel CPUは毎年新しい命令を追加する
• 新・旧両対応
• 解決方法
• JITアセンブラを使う
DNNの事情
12 / 69

13. • C++でx64のコードをJIT生成できるライブラリ
• https://github.com/herumi/xbyak
• 使い方
• Xbyak::CodeGeneratorクラスを継承する
• クラス内でx86/x64ニーモニックに対応する関数を呼び出す
• コード生成された関数のアドレスを取得して呼び出す
Xbyak
struct Code : Xbyak::CodeGenerator {
Code() {
mov(eax, 3);
ret();
}
};
Code c;
auto f = c.getCode<int (*)()>();
printf("x=%d¥n", f()); // x=3
13 / 69

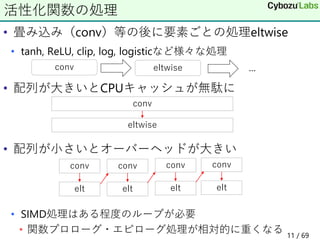
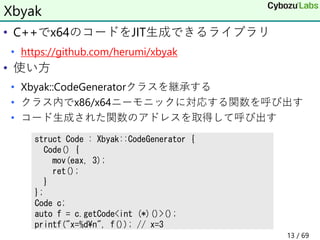
14. • 基本的にIntelのアセンブラ形式
• C++の文法を使った名前づけ
• ラベルクラス
• 前方参照 後方参照
XbyakのDSL概略
auto src = rsi;
auto i = rcx;
auto x = rax;
mov(x, ptr[src+i*4]);
アセンブラ Xbyak
add rax, rcx add(rax, rcx); // rax += rcx
mov eax, dword [rbx+rcx*8+4] mov(eax, ptr[rbx+rcx*8+4]);
auto lp = L();
...
sub(n, 1);
jnz(lp);
Label exitL;
jmp(exitL);
...
L(exitL);
14 / 69

15. • uint32_t src[n];の要素の和を求める関数を生成
• （nが小さいとき）
• 実行時に決まる様々なパラメータに応じた
コード生成と実行するプログラムを記述可能
コード生成の例
struct Code : Xbyak::CodeGenerator {
Code(int n) {
mov(eax, ptr[src]);
for (int i = 1; i < n; i++) {
add(eax, ptr[src + i * n]);
}
}
};
mov eax, ptr[rcx]
mov eax, ptr[rcx]
add eax, ptr[rcx+4]
mov eax, ptr[rcx]
add eax, ptr[rcx+4]
add eax, ptr[rcx+8]
Code c(1); Code c(2); Code c(3);
15 / 69

16. • パラメータに応じて最適な順序を選択
多重ループの順序
void pick_loop_order(jit_conv_conf_t &jcp) {
jcp.loop_order = loop_cwgn;
if (jcp.ngroups > 1) {
jcp.loop_order = loop_ngcw;
if (jcp.mb < jcp.nthr)
jcp.loop_order = jcp.ndims == 3 ? loop_nwcg : loop_nhwcg;
} else if (jcp.mb >= jcp.nthr && jcp.ic_without_padding <= 8) {
jcp.loop_order = loop_ngcw;
}
選択されたパターンに応じた
ループコードを生成
16 / 69

17. • oneDNNでは畳み込みの後の操作を合成するAPIがある
• https://oneapi-src.github.io/oneDNN/dev_guide_attributes_post_ops.html
• サポートされているもの(post-ops)
• eltwise, 要素ごとの操作, sum ; reduction
• depthwise ; 1x1畳み込み専用, binary ; 1bitデータ操作
• それらのコード片をconvの最後に挿入
• 関数の退避・復元の回数を減らせる
処理の合成
convのコード生成最後のあたり expのコード生成部
挿入
17 / 69

18. • 富岳（A64FX）用のXbyak
• 富岳もIntelと同じくSIMDベースのアーキテクチャ（SVE）
• TensorFlowやPyTourchを使いたいのでoneDNNを移植する
• Xbyak_translator
• Intel用に記述されたAVX-512用コード生成プログラムを
富岳のSVE用コード生成プログラムに（半）自動変換
• 詳細はhttps://blog.fltech.dev/entry/2020/11/18/fugaku-onednn-deep-dive-ja
Xbyak_aarch64
18 / 69

19. • 処理の中心は多数のパラメータを持つ
大きな多次元配列の積和演算とスカラー演算
• 静的には（C++的には）最適化しづらい
• JITアセンブラの導入でパラメータに応じた
最適なコードを動的生成する
oneDNNのまとめ
19 / 69

20. AVX-512の基本

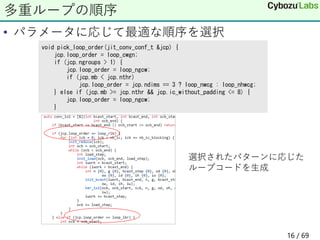
21. • Intelの512bit SIMD命令セット
• 512bitのレジスタ32個zmm0, ..., zmm31
• 64bit整数x8, 32bit整数x16, 16bit整数x32, 8bit整数x64
• 64bit double x 8, 32bit float x 16
• 基本的に
• 「≪命令≫ dst, src1, src2」の形 ; dst←「src1とsrc2で計算」
• 例
• vaddps z, x, y ; z = x + y as float
• vpaddd z, x, y ; z = x + y as int
• 𝑥 = [𝑥0: … : 𝑥15], 𝑦 = [𝑦0: … 𝑦15]
AVX-512
𝒙 𝒙𝟎 𝒙𝟏 ... 𝒙𝟏𝟓
𝑦 𝑦0 𝑦1 ... 𝑦15
𝑧 𝑥0 + 𝑦0 𝑥1 + 𝑦1 ... 𝑥15 + 𝑦15
21 / 69

22. • 整数 ; vp ≪演算≫≪要素の型≫ dst, src1, src2
• d(dword x 32)として要素ごとにzmm2 = zmm1 + zmm0
• q(qword x 16)として要素ごとにzmm2 = zmm1 – zmm0
• 浮動小数点数 ; v≪演算≫≪要素の型≫ dst, src1, src2
• pd(double x 16)として要素ごとにzmm2 = zmm1 * zmm0
• ps(float x 32)として要素ごとにzmm2 = zmm1 / zmm0
基本演算の例
vpaddd zmm2, zmm1, zmm0
vpsubq zmm2, zmm1, zmm0
vmulpd zmm2, zmm1, zmm0
vdivps zmm2, zmm1, zmm0
22 / 69

23. • 𝑤 = 𝑥 × 𝑦 + 𝑧
• 行列計算などで多用される
• 𝑡 = 𝑥 × 𝑦, 𝑤 = 𝑡 + 𝑧とするよりも誤差が小さくなり得る
• 4タイプ
• vfmadd 𝑥, 𝑦, 𝑧 ; 𝑥 × 𝑦 + 𝑧
• vfmsub 𝑥, 𝑦, 𝑧 ; 𝑥 × 𝑦 − 𝑧
• vfnmadd 𝑥, 𝑦, 𝑧 ; −𝑥 × 𝑦 + 𝑧
• vfnmsub 𝑥, 𝑦, 𝑧 ; −𝑥 × 𝑦 − 𝑧
• 3個のレジスタ入力なのでAVXは番号でソースを指定
• vfmadd312 𝑥1, 𝑥2, 𝑥3 ; 𝑥1 = 𝑥3 × 𝑥1 + 𝑥2
• vfmadd213 𝑥1, 𝑥2, 𝑥3 ; 𝑥1 = 𝑥2 × 𝑥1 + 𝑥3
積和演算
23 / 69

24. AVX-512のDNN向け命令

25. • vpdpbusd dst, u, s
• 今まではvpmaddubsw+vpmaddwd+vpadddを使っていた
8bit整数の積和演算
void vpdpbusdC(int dst[16], const uint8_t u[64], const int8_t s[64])
{
dst[ 0]+=u[ 0]*s[ 0]+u[ 1]*s[ 1]+u[ 2]*s[ 2]+u[ 3]*s[ 3];
dst[ 1]+=u[ 4]*s[ 4]+u[ 5]*s[ 5]+u[ 6]*s[ 6]+u[ 7]*s[ 7];
dst[ 2]+=u[ 8]*s[ 8]+u[ 9]*s[ 9]+u[10]*s[10]+u[11]*s[11];
...
dst[15]+=u[60]*s[60]+u[61]*s[61]+u[62]*s[62]+u[63]*s[63];
}
if (support_vnni) { // 実行時にCPU判別して命令の切り換え
vpdpbusd(dst, src1, src2); // dst += src1 * src2
} else {
vpmaddubsw(tmp, src1, src2);// [a0 b0+a1 b1:a2 b2+a3 b3:...] 8->16
vpmaddwd(tmp, ones, tmp); // [a0 b0+a1 b1+a2 b2+a3 b3:...]16->32
vpaddd(dst, dst, tmp);
}
25 / 69

26. • float精度が必要ない箇所でデータサイズを半分にする
• メモリ転送の効率がよくなる
• 16bitの浮動小数点数の型は他のタイプもある
• IEEE754のbinary16(fp16)は指数部5bit, 仮数部10bit
• bloat16よりも扱える数の範囲は狭く精度は高い
• ARMはbinary16
• GoogleのTPUはbfloat16
bfloat16
型 符号ビット(s) 指数部(e) 仮数部(f) 値
float 1 8 23
−1 𝑠
2𝑒−127
1 +
𝑓
224
bfloat16 1 8 7
−1 𝑠
2𝑒−127
1 +
𝑓
28
26 / 69

27. • 指数部が同じなので
• bfloat16→floatは下位16bit zeroを追加すればOK
• float→bfloat16は上位16bitを取り出せばOK
• 丸め処理を入れると若干精度がよくなる
floatとbfloat16の相互変換
bf16 float2bf16(float f) {
// ignore denormal and infinity
uint32_t u = f2u(f);
uint32_t rounding = 0x7fff + ((u >> 16) & 1);
u += rounding;
return bf16(u >> 16);
}
27 / 69

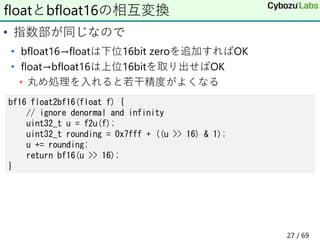
28. • vcvtne2ps2bf16 dst, src1, src2
• src1, src2のfloatをbfloat16にして連結してdstに
• vdpbf16ps dst, src1, src2 ; 積和命令(結果はfloat)
• これらの命令をサポートしていれば利用
AVX-512のbloat16関連命令
void vcvtne2ps2bf16(
bf16 dst[32], const float src1[16], const float src2[16]) {
for (int i = 0; i < 16; i++) {
dst[i] = float2bf16(src1[i]);
dst[i+16] = float2bf16(src2[i]);
} }
void vdpbf16ps(
float dst[16], const bf16 src1[32], const bf16 src2[32]){
for (int i = 0; i < 16; i++) {
dst[i] += bf16_to_float(src1[i*2+0])*bf16_to_float(src2[i*2+0]);
dst[i] += bf16_to_float(src1[i*2+1])*bf16_to_float(src2[i*2+1]);
} }
28 / 69

29. AVX-512によるlogの実装

30. • log 1 + 𝑥 = 𝑥 −
1
2
𝑥2 +
1
3
𝑥3 −
1
4
𝑥4 + ⋯を使う
• この関数は精度を上げるにはたくさん項が必要
• できるだけ減らしたい
• float(32bit浮動小数点数)のbit表現
• 32bitを符号1bit, 指数部8bit, 仮数部23bitに分ける
• 𝑥 = −1 𝑠2𝑒−127(1 +
𝑓
224), e:指数部, f:仮数部
• 𝑥 = 2𝑛𝑦の形(1 ≤ 𝑦 < 2, 𝑛 ∈ ℤ)
• log 𝑥 = log 2𝑛𝑦 = 𝑛𝑙𝑜𝑔 2 + log(𝑦)
• log(𝑦), 1 ≤ 𝑦 < 2だけ計算すればよい
log(𝑥)の計算
s(1) e(8) f(23)
30 / 69

31. • 式変形して範囲を少し狭める
• 𝑎 =
2
3
𝑦 − 1とすると 𝑎 ≤ 1/3となる
• 𝑦 = 1.5(1 + 𝑎)だからlog 𝑦 = log 1.5 + log(1 + 𝑎)
• ここで多項式近似を使う
• floatの精度は23bit程度
• 𝑎 = 1/3のときlog 1 + 𝑎 = 𝑎 −
1
2
𝑎2 + ⋯がそれに達するには
9次ぐらいまで足せばよい
• まとめる
• 𝑥 = 𝑦2𝑛, 𝑦 = 1.5(1 + 𝑎)として
• log 𝑥 = log 𝑦2𝑛 = 𝑛𝑙𝑜𝑔 2 + log 𝑦
= 𝑛𝑙𝑜𝑔 2 + log 1.5 + log(1 + 𝑎)
log(𝑦)の計算
31 / 69

32. • floatとintのbit表現の入れ換え
• tbl[i] = 1/(i+1) for i = 0, ..., 8を事前計算
• s=0, e=127なら𝑦 = −1 𝑠2𝑒−127 1 +
𝑓
224 = 1 + 𝑓/224
Cでの実装例
float log(float x) {
uint32_t u = f2u(x);
float n = int(u - (127 << 23)) >> 23; // x = y 2^n のnを取り出す
u = (u & 0x7fffff) | (127 << 23);
float y = u2f(u); // yを取り出す
float a = (2/3) * y - 1
n = n * log2 + log(1.5);
x = tbl[8];
for (int i = 7; i >= 0; i--) x = x * a + tbl[i];
return x * a + n;
}
float f2u(uint32_t x) { float y; memcpy(&y, &x, 4); return y; }
uint32_t u2f(float x) { uint32_t y; memcpy(&y, &x, 4); return y; }
32 / 69

33. • 各種定数は事前にレジスタに設定しておく
• 分かりやすさのため下記コードは定数はそのまま表記({}つき)
• 実際はその値を代入したレジスタ
• input/output : zm0
• zm1, zm2を利用
AVX-512を使った実装例
vpsubd(zm1, zm0, {127 << 23}); // u32として127 << 23を引く
vpsrad(zm1, zm1, 23); // 右23bitシフトしてnを取り出す
vcvtdq2ps(zm1, zm1); // nをfloatに変換
vpandd(zm0, zm0, {0x7fffff});
vpord(zm0, zm0, {127 << 23}); // x=y 2^nのyを取り出す
vfmsub213ps(zm0, {2/3}, {1}); // a = y * (2/3) - 1
vfmadd213ps(zm1, {log2}, {log(1.5)}); // n = n * log2 - log(1.5)
vmovaps(zm2, tbl[8]); // x = 1.0
for (int i = 7; i >= 0; i--) vfmadd213ps(zm2, zm0, tbl[i]);
vfmadd213ps(zm0, zm2, zm1); // x * a + n
33 / 69

34. • n個のfloat配列に対する処理方法
• まず16個ずつSIMD処理する
• ループアンロール（後述）するときは16の倍数
• 端数処理の前にマスクレジスタについて説明する
ループ処理
// n, src, dstはレジスタのalias
mov(ecx, n);
and_(n, ~15u); // nを超えない最大の16の倍数
jz(mod16); // nが0になれば端数処理へ
Label lp = L();
vmovups(zmm0, ptr[src]); // 16個読み込む
add(src, 64); // srcレジスタを64byte増やす
// log一つ分の処理をここで行う
vmovups(ptr[dst], zmm0); // 結果を書き込む
add(dst, 64); // dstレジスタを64byte増やす
sub(n, 16); // カウンタを16減らす
jnz(lp); // 0になるまでループ
34 / 69

35. • 64bitのk1, ..., k7の7個
• SIMDレジスタの各要素についてどの要素を処理するか指定
• k0は計算はできるがマスクレジスタ指定には使えない
• マスクレジスタの扱い
• 該当bitが1 ; 該当要素の処理が行われる
• 該当bitが0
• ゼロ化マスクなし
• 操作は行われない（例外や違反は発生しない）
• ゼロ化マスクあり
• 0で埋められる
マスクレジスタ
35 / 69

36. • vmovdqu8（byte単位のレジスタコピー）
• k1レジスタのビットが立っているところだけコピー
マスクの例
[Xf Xe Xd Xc Xb Xa X9 X8 X7 X6 X5 X4 X3 X2 X1 X0]
xmm0
[Yf Ye Yd Yc Yb Ya Y9 Y8 Y7 Y6 Y5 Y4 Y3 Y2 Y1 Y0]
xmm1
[ 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0]
k1
[Yf Ye Yd Yc Yb Ya Y9 Y8 Y7 Y6 Y5 X4 Y3 Y2 X1 Y0]
xmm1
vmovdqu8 xmm1{k1}, xmm0
36 / 69

37. • vmovdqu8（byte単位のレジスタコピー）
• k1レジスタのビットが立っているところだけコピー
• それ以外は0クリア
• XbyakではT_zで指定する
ゼロ化マスクの例
[Xf Xe Xd Xc Xb Xa X9 X8 X7 X6 X5 X4 X3 X2 X1 X0]
xmm0
[Yf Ye Yd Yc Yb Ya Y9 Y8 Y7 Y6 Y5 Y4 Y3 Y2 Y1 Y0]
xmm1
[ 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0]
k1
[00 00 00 00 00 00 00 00 00 00 00 X4 00 00 X1 00]
xmm1
vmovdqu8 xmm1{k1}{z}, xmm0
37 / 69

38. • 複数の条件のandやorを効率よく計算するために
マスクレジスタの演算命令が追加されている
• k≪演算≫{b,w,d,q} dst, src1, src2の形
• add, and, or, not, xor
• andn(x, y) := ~(x & y)
• xnor(x, y) := ~(x ^ y)
• shiftl, shiftrなど
• ZF, CF制御系
• kortest{b,w,d,q} src1, src2
• (src1 | src2) == 0ならZF = 1
• (src1 | src2) == ~0ならCF = 1
• vcomiss x, yよりvcomiss k, x, y; kortest k, kの方が速いらしい
マスクレジスタの演算
38 / 69

39. • 先程の16単位で処理した残り（n<16）
• 読み書きするデータは残りn個（n = 7の例）
ループの端数処理
L(mod16); // 端数処理時のジャンプ先
and_(ecx, 15); // ecx = n = n & 15
jz(exit); // 0ならexitにジャンプ
mov(eax, 1); // eax = 1
shl(eax, cl); // eax = 1 << n
sub(eax, 1); // eax = (1 << n) - 1 ; n個の1bit
kmovd(k1, eax); // k1に設定
vmovups(zmm0|k1|T_z, ptr[src]); // srcからn個の要素を読む
// log一つ分の処理
vmovups(ptr[dst]|k1, zm00); // n個書き込む
L(exit);
+0 +1 +2 +3 +4 +5 +6|+7 +8 +9 +a +b +c +d +e +f
[x0 x1 x2 x3 x4 x5 x6 -- -- -- -- -- -- -- -- --]
k1 1 1 1 1 1 1 1 0 0 0 0 ...
39 / 69

40. • この実装は区間[2, 3]で相対誤差eの最大値は1.7e-7
• e=(x-真の値)/真の値
• 区間[0.99, 1.01]では4.2e-2とかなり悪い
• 何故?log(𝑥)は𝑥が1に近いとき0に近い
• log 𝑥 = 𝑛𝑙𝑜𝑔 2 + log 1.5 + log(1 + 𝑎)
• 計算途中で桁落ちして精度低下
• 𝑥 = 1 + 𝜖(𝜖が小さい)ならlog 𝑥 = log(1 + 𝜖)で計算すべき
精度向上
// aとnを計算
if (abs(x - 1) < 1/32) { // 追加すべきコード
n = 0;
a = x - 1;
}
return n + log(1+a);
40 / 69

41. • 分岐はSIMDで扱いづらい
• マスクレジスタを利用して分岐を表現する
• 区間[0.99, 1.01]で4.2e-2→1.2e-7と劇的に精度向上
SIMD化
// 数値リテラルは事前にレジスタに代入しておく
vmovapx(keepX, zmm0); // xの値を保持
...(計算)...
vsubps(zmm2, keepX, {1}); // x-1
vandps(zmm2, zmm2, {0x7fffffff}); // |x-1|
vcmpltps(k2, zmm2, {1/32}); // k2 = |x-1| < 1/32
vsubps(zmm0|k2, keepX, {1}); // if (k2) y = x-1
vxorps(zmm3|k2, zmm3); // if (k2) h = 0
x 1.5 1.01 2.3 1.001 ...
k2 0 1 0 1 ...
41 / 69

42. • Xeon 8280 2.7GHz
• float x[16384];に対する1ループ(16要素)あたりの時間(nsec)
• gcc-9.3.0 -O3
• -Ofastにするとstd::logもSIMD化されて8.7nsecに
ベンチマーク
std::log fmath::log
初版 56.2 4.0
精度向上版 56.2 5.3
42 / 69

43. SVEの基本とlogの実装

44. • 富士通が開発したスパコン富岳用CPU
• Arm v8-A命令セット+SVEを採用した最初のCPU
• SVE ; SIMD命令セット
• https://developer.arm.com/documentation/ddi0596/2020-12/SVE-Instructions
• https://github.com/fujitsu/
• A64FXでは32個の512-bit SIMDレジスタ ; z0, ..., z31
• int8 x 64, int32 x 16, float x 16, double x 8など
様々なデータ型の並列処理が可能
• レジスタ名にサフィックスを付けて型のbitを表す
• z0.d(64bit), z0.s(32bit), z0.b(8bit)など
• 16個の述語(predicate)レジスタ ; p0, ..., p15
• マスクレジスタ相当
• 1なら処理, 0なら処理しない
A64FX
44 / 69

45. • 2引数のop操作
• 出力と1引数のop操作+述語タイプ
• 出力と2引数のop操作+述語タイプ
• movprfx (dstをsrcとして利用する命令の補助)
• 3引数タイプの積和に変換
• movprfxはμOPレベルでは
pack処理されて一つのアーキテクチャ命令になる
SVEの命令概略
op(dst, src1, src2); // dst = op(src1, src2);
op(dst, pred, src); // dst = op(dst, src) with pred
op(dst, pred, src1, src2); // dst = dst * src1 + src2
movprfx(dst, src3);
fmadd(dst, pred, src1, src2); // dst = src3 * src1 + src2
45 / 69

46. • 符号の位置によって8パターンある
• fmad(a, b, c) ; a = a * b + c
• fmsb(a, b, c) ; a =-a * b + c
• fmla(a, b, c) ; a = a + b * c
• fmls(a, b, c) ; a = a - b * c
• 上記の符号反転
• fnmad(a, b, c); a =-a * b - c
• fnmsb(a, b, c); a = a * b - c
• fnmla(a, b, c); a =-a - b * c
• fnmls(a, b, c); a =-a + b * c
積和命令
46 / 69

47. • input/output : z0, use z1, z2
• 定数は事前にレジスタに入れておく
• p0はptrue(p0.s);により全て1にしておく
SVEを使ったlogの実装例
sub(z1.s, z0.s, {127 << 23}); // intとしてz1 = z0 - (127 << 23)
asr(z1.s, z1.s, 23); // z1 = int(z1) >> 23
scvtf(z1.s, p0, z1.s); // z1 = float(z1)
and_(z0.s, p0, {0x7fffff}); // z0 = x & 0x7fffff
orr(z0.s, p0, {127 << 23}); // y = (x & 0x7fffff) | (123 << 23)
fnmsb(z0.s, p0, {2/3}, {1.0}); // z0 = z0 * (2/3) - 1
fmad(z1.s, p0, {log2}, {log1p5}); // z1 = n = z1 * log2 + log(1.5)
movprfx(z2.s, p0, tbl[8]);
fmad(z2.s, p0, z0.s, tbl[7]);
for (int i = 6; i >= 0; i--) fmad(z2.s, p0, z0.s, tbl[i].s);
fmad(z0.s, p0, z2.s, z1.s); // z0 = x * a + n
47 / 69

48. • n個のfloat配列に対するSIMD処理のループ
• src, dst, nは汎用レジスタのalias
• 𝑛 ≥ 16の間ループする
ループ処理
Label skip;
b(skip);
Label lp = L();
ld1w(z0.s, p0/T_z, ptr(src)); // srcアドレスからz0に読み込む
add(src, src, 64); // src更新
// log 1個分の処理
st1w(z0.s, p0, ptr(dst)); // logの値をdstに書き込む
add(dst, dst, 64); // dst更新
sub(n, n, 16); // n -= 16
L(skip);
cmp(n, 16);
bge(lp); // n >= 16ならlpへジャンプ
48 / 69

49. • whilelt (p.s, x5, n);
• マスクレジスタpについてp[i] = (x5+i < n) for i = 0, ...
• b_first(lp);
• x5 < nならlpにジャンプ
ループの端数処理
Label cond;
mov(x5, 0); // x5をインデックスiとして使う
b(cond);
Label lp2 = L();
ld1w(z0.s, p0/T_z, ptr(src, x5, LSL, 2)); // z0 = src[x5 << 2]
// log 1個分の処理
st1w(z0.s, p0, ptr(dst, x5, LSL, 2)); // dst[x5 << 2] = z0
incd(x5); // x5 += 16
L(cond);
whilelt(p0.s, x5, n);
b_first(lp2);
49 / 69

50. • 分岐処理（再掲）
• AVX-512と違うところ
• fcpyはいくつかの定数1, 0.5, 1/8などは即値で扱える
• facgeは絶対値を取った比較ができる(vrangepsは違った...)
精度向上の処理部分
fsub(z2.s, x.s, one.s); // z2 = x-1
fcpy(tmp.s, p0, 1.0/8); // tmp = 1/8
facge(p1.s, p0, tmp.s, z2.s); // p1 = 1/8 >= abs(x-1) ; 要素ごと
mov(a.s, p1, z2.s); // 条件成立ならa = x-1
eor(n.s, p1, n.s); // 条件成立ならn = 0 ; eor = xor
// aとnを計算
if (abs(x - 1) < 1/32) { // 追加すべきコード
n = 0;
a = x - 1;
}
return n + log(1+a);
50 / 69

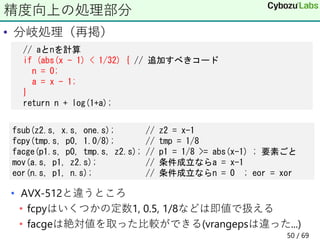
51. • FX700 2.0GHz?
• float x[16384];に対する1ループ(16要素)あたりの時間(nsec)
• gcc-8.4.1 -O3
ベンチマーク
std::log fmath::log
初版 256.4 20.23
精度向上版 256.4 23.29
51 / 69

52. • 𝑐について
• 𝑓を1/𝑐の近似値とすると𝑔 ≔ 𝑓𝑐 − 1は0に近い
• 𝑐 = (1 + 𝑔)/𝑓だからlog 𝑐 = log 1 + 𝑔 − log(𝑓)
• 𝑓とlog(𝑓)をテーブルルックアップする
• 近似値の取り方
• 仮数部を使うには1以上2未満の範囲に入る必要がある
• 今扱いたい区間は1の付近（< 1と≥ 1で不連続なので避ける）
• 区間[0.9, 1.1]は[0.9×1.4, 1.1×1.4]になる
• 𝑎 ≔ 2𝑥 = 𝑏2𝑛
, 𝑐 ≔ Τ
𝑏 2とすると|log(𝑐)| ≤ 𝑙𝑜𝑔 2
• f2u(b)の仮数部の上位5bitをインデックスdとして
• T1[d] = 2/𝑏, T2[i]=log(T1[d])とする
• L=5のとき𝑔~1/32なのでlog(1 + 𝑔)は3次近似でよい
テーブルを使うアルゴリズム(1/2)
52 / 69

53. • 擬似コード
テーブルを使うアルゴリズム(2/2)
input : x
a = sqrt(2) x
a = b 2^nと分解する (1 <= b < 2)
c = (1/sqrt(2)) bとすると(1/sqrt(2) <= c < sqrt(2))
L = 5
d = (f2u(b) & mask(23)) >> (23 - L) // bの上位L bitを取り出す
// T1[i] = sqrt(2) / u2f((127 << 23) | (i << (23 - L)))
// T2[i] = log(T1[i])
f = T1[d] は 1/c = sqrt(2) / bの近似値
g = f c - 1 とすると |g| <= 1/2^L
log c = log ((1 + g)/f) = log(1+g) - log f
h = T2[d] は log f
log x = log (c * 2^n)
= n log 2 + log c = n log 2 - log f + log(1+g)
53 / 69

54. • テーブル引きy = tbl[x]のSIMD版
• SVE
• zにindexの4倍(floatだから)を入れる, xはtblのアドレス
• AVX-512
• マスクレジスタ必須 xnord(xor + not)で全て1にする
• zにindexを入れる, raxはtblのアドレス
• 実験コードは
• https://github.com/herumi/fmath/ のfmath2.hpp
• https://github.com/herumi/misc/sve/ のlog.hppなど
gather命令
ld1w(y.s, p0, ptr(x, z.s, SXTW));
kxnord(k2, k2, k2);
vgatherdps(y|k2, ptr[rax + z * 4]);
54 / 69

55. • AVX-512とSVEで実装してみた
• コンパイラなどは前と同じ
• AVX-512では大分遅くなった
• SVEでは効果あり
• AVX-512はパイプラインが相対的に短く
FMAで通した方がよさそう?
• テーブルサイズを32→16にしてgatherじゃなくてpermを使う
とよりよい?
ベンチマーク
AVX-512 SVE
std::log 56.2 256.4
初版 4.0 16.67
精度向上あり 5.3 20.43
gather版+精度向上 8.57 17.88
55 / 69

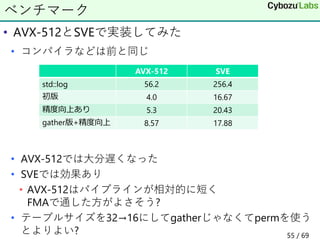
56. • SVEでループアンロール(N = 1, 2, 3)してみた
• 16要素ごとではなく16x2, 16x3要素ごと処理
• これが
• こんな感じになる
• 元がC個レジスタを使うならCN個のレジスタt[CN]を用意
ループアンロール(1/2)
sub(z1.s, z0.s, {127 << 23});
asr(z1.s, z1.s, 23);
scvtf(z1.s, p0, z1.s);
and_(z0.s, p0, {0x7fffff});
#define UNROLL for (int i = 0; i < N; i+=C)
UNROLL sub(t[i+1].s, t[i+0].s, {127 << 23});
UNROLL asr(t[i+1].s, t[i+1].s, 23);
UNROLL scvtf(t[i+1].s, p0, t[i+1].s);
UNROLL and_(t[i+0].s, p0, {0x7fffff});
生成コード
sub(z1.s, z0.s, {127 << 23});
sub(z4.s, z3.s, {127 << 23});
sub(z7.s, z6.s, {127 << 23});
asr(z1.s, z1.s, 23);
asr(z4.s, z4.s, 23);
asr(z7.s, z7.s, 23);
...
56 / 69

57. • 各命令を並列化してSVEでベンチマーク
• gather版はunroll = 3で逆に遅くなった
• パイプラインがつまった?
• gatherなし版はunrollの効果が大きい
• パイプラインが長いせいと思われる
• logではなくexpだがAVX-512ではそこまで効果は無かった
（ので実装していない）
ループアンロール(2/2)
gatherなし(精度向上) gatherあり(精度向上)
unroll = 1 16.67(20.43) 17.79(17.88)
unroll = 2 13.48(15.64) 12.88(13.91)
unroll = 3 10.25(12.47) 14.61(14.94)
57 / 69

58. SVEレジスタの依存関係解消

59. • 去年の第9回HPC-Phys勉強会での問いかけ p.26
• https://www.slideshare.net/herumi/hpc-phys20201203
問題の発端
pture(p0.s); // 全て1
Label lp = L();
ld1w(z0.s, p0/T_z, ptr(src1, idx, LSL, 2));
ld1w(z1.s, p0/T_z, ptr(src2, idx, LSL, 2));
frintm(z2.s, p0, z0.s); // floor
// fadd(z2.s, z0.s, z0.s);
fadd(z0.s, z1.s, z2.s);
frecpe(z1.s, z0.s);
frecps(z2.s, z0.s, z1.s);
fmul(z1.s, z1.s, z2.s);
frecps(z2.s, z0.s, z1.s);
fmul(z0.s, z1.s, z2.s);
st1w(z0.s, p0, ptr(out, idx, LSL, 2));
add(idx, idx, 16);
cmp(idx, n);
blt(lp);
frecpe(z1.s, z0.s);
frecps(z3.s, z0.s, z1.s);
fmul(z1.s, z1.s, z3.s);
frecps(z3.s, z0.s, z1.s);
fmul(z0.s, z1.s, z3.s);
コード内容は本質ではないので略
1. z2をz3に変えたら51clkが11clkになった
何故?
2. frintmをfaddに変えるだけでも
51clk→11clk 59 / 69

60. • 結果、A64FX Microarchitecture Manualが更新された
富士通の人が調べてくれた
60 / 69

61. • predあり命令は基本merge
• frintm(z2.s, p0, z0.s)は「z2とz0の結果」でz2を更新
• p0=trueでもz2の結果※を待つ→遅くなる
• z2をz3にする→frintmのz2は待たなくてよい→速くなる
依存関係
Label lp = L();
ld1w(z0.s, p0/T_z, ptr(src1, idx, LSL, 2));
ld1w(z1.s, p0/T_z, ptr(src2, idx, LSL, 2));
frintm(z2.s, p0, z0.s); // floor
// fadd(z2.s, z0.s, z0.s);
fadd(z0.s, z1.s, z2.s);
frecpe(z1.s, z0.s);
frecps(z2.s, z0.s, z1.s);
fmul(z1.s, z1.s, z2.s);
frecps(z2.s, z0.s, z1.s); // ※
fmul(z0.s, z1.s, z2.s);
st1w(z0.s, p0, ptr(out, idx, LSL, 2));
...
61 / 69

62. • frintm(z2.s, p0, z0.s);
• predありなので依存関係発生
• fadd(z2.s, z0.s, z0.s);
• predなしなので依存関係は発生しない
• predありのfadd命令fadd(z2.s, p0, z0.s);にしたら51clk!
• でもfrintmにはpredなし命令は存在しない
addにしたら速くなった訳
62 / 69

63. • 先程のマニュアル再掲
• >なお、MOVPRFX 命令の修飾にて Zeroing predication を指示
することで、ディスティネーション・レジスタのソース・オ
ペランドとしての使用を抑止することができる。
• movprfxの挿入で依存関係を切る
• これで51clk→11clkになった
• predつきのmovprfxでもよい（デフォルトT_z）
• mov(z2.s, 0);でも依存関係は切れるがμOPは消費する
• eor(z2.d, z2.d, z2.d);は駄目（x64ならzero idiomで切れる）
• eor(z2.d, z0.s, z0.s);は少し遅いけどOK（うーむ）
• p0=all trueのときに依存関係を切るパスがあれば...
movprfxを使う
frintm(z2.s, p0, z0.s);
movprfx(z2, z0);
frintm(z2.s, p0, z0.s);
63 / 69

64. • float配列に対するexpの実装
• https://github.com/herumi/misc/blob/master/sve/fmath-sve.hpp
exp(x)の実装でも同様の現象に遭遇
Label lp = L();
ld1w(z0.s, p0/T_z, ptr(src));
add(src, src,);
fmin(z0.s, p, para.expMax.s);
fmax(z0.s, p, para.expMin.s);
fmul(z0.s, z0.s, para.log2_e.s);
movprfx(z1, z0); // clear implicit dependency
frintm(z1.s, p, z0.s); // floor : float -> float
fcvtzs(z2.s, p, z1.s); // n = float -> int
fsub(z1.s, z0.s, z1.s); // a
fadd(z0.s, z1.s, para.one.s); // b = 1 + a
lsr(z1.s, z0.s, 17); // bL
fexpa(z1.s, z1.s); // c = fexpa(bL)
fscale(z1.s, p, z2.s); // z1 *= 2^n
and_(z2.d, z0.d, para.not_mask17.d);
fsub(z2.s, z0.s, z2.s); // z
movprfx(z0.s, p, para.coeff2.s);
fmad(z0.s, p, z2.s, para.coeff1.s);
fmad(z0.s, p, z2.s, para.one.s);
fmul(z0.s, z1.s, z0.s);
st1w(z0.s, p0, ptr(dst));
add(dst, dst, 64);
sub(n, n, 16);
L(skip);
cmp(n, 16);
bge(lp);
movprfxの挿入でループあたり
25nsec→15nsec
予想より遅い
or レジスタを入れ換えて速度が変わった
→ 依存関係の確認を
64 / 69

65. • predあり・なし選択可能
• add, sub, fadd, fmul, fsub, and, asr, bic, eor, fmov, lsl, lsr, orr等
• predありのみ
• abs, cls, clz, cnot, cpy, fabd, fmad, fmin, fmax, frintn等
• 依存関係に気をつけるべき命令群
• predあり命令はmergeのみ
• 例外
• movprfxのみzero/mergeを選択可能
• load系（lz1wなど）はpredありでzero
• store系（st1wなど）はpredありで何もしない（merge相当）
predあり・なし命令
65 / 69

66. Intel AMX

67. • AVXと異なる新しい行列演算アクセラレータ
• 8個の新しいレジスタtmm0, ..., tmm7（1個1KiB）
• 今のところbfloat16とint8専用
• タイル
• メモリの大きな2次元行列の部分行列を表す2次元のレジスタ
• TMUL（tile matrix multiply unit）
• タイル行列乗算ユニット
Intel AMX (on Sapphire Rapids)
x64がタイルコマンドを発行
アクセラレータが計算を実行
メモリの一貫性は保持
Intel Architecture Instruction Set Extensions and Future Features Programming Reference
67 / 69

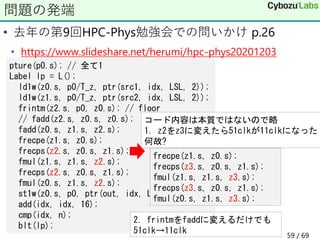
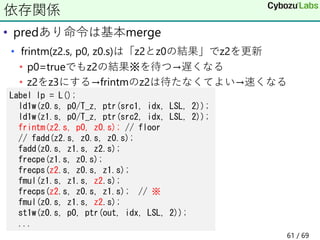
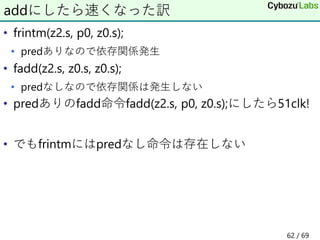
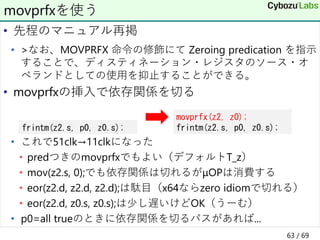
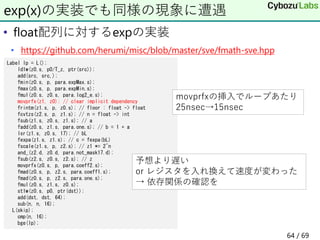
68. • tileloadd tmm, [base+offset+stride]
• 部分行列の読み込み
• tmm ; タイルレジスタ
• sibmemという特殊なメモリアドレッシング
• base ; 行列の先頭アドレスを指すレジスタ
• offset ; ターゲットの計算位置を表す定数
• stride ; 次の列への差分を指すレジスタ
命令概要
tmm base+offset memory
stride
68 / 69

69. • 最内ループ
https://github.com/oneapi-src/oneDNN/blob/master/src/cpu/x64/brgemm/jit_brgemm_kernel.cpp
行列の積和C += ABの一部
tileloadd tmm0, [baseC+strideC]
tileloadd tmm1, [baseC+strideC+offset]
mov n, 0
lp:
tileloadd tmm2, [baseA+strideA]
tileloadd tmm3, [baseB+strideB]
// u8成分のAとs8成分のBの行列計算してtmm0に足し込む
tdpbusd tmm0, tmm2, tmm3
tileloadd tmm3, [baseB+strideB+offset] // 隣のB
tdpbusd tmm1, tmm2, tmm3 // 隣のCの積和
add baseA, k // 次のA
add baseB, k*strideB
add n, k
cmp n, limit
jne lp
tilestored [baseC+strideC], tmm0 // Cの更新
tilestored [baseC+strideC+m], tmm1 // 隣のCの更新
tmm0 tmm1 tmm2 tmm3
69 / 69