More Related Content
PDF
PDF
LLVMで遊ぶ(整数圧縮とか、x86向けの自動ベクトル化とか) PDF
PDF
PPTX
PDF
ARM CPUにおけるSIMDを用いた高速計算入門 PDF
PDF
What's hot
PDF
PDF
PDF
PDF
PDF
PDF
[GTCJ2018]CuPy -NumPy互換GPUライブラリによるPythonでの高速計算- PFN奥田遼介 PDF
PPTX
【LT資料】 Neural Network 素人なんだけど何とかご機嫌取りをしたい PPTX
画像処理ライブラリ OpenCV で 出来ること・出来ないこと PDF
PDF
最近のSingle Shot系の物体検出のアーキテクチャまとめ PDF
PDF
PDF
PPTX
PPTX
PDF
PDF
PDF
PPTX
Viewers also liked
PDF
PDF
A x86-optimized rank&select dictionary for bit sequences PDF
JIT Code Profiling with VTune PPTX
PDF
AVX2時代の正規表現マッチング 〜半群でぐんぐん!〜 PDF
PDF
PDF
MS Officeファイル暗号化のマスター鍵を利用したバックドアとその対策 PDF
PDF
PDF
汎用性と高速性を目指したペアリング暗号ライブラリ mcl PDF
PDF
Similar to Haswellサーベイと有限体クラスの紹介
PDF
PDF
Intel GoldmontとMPXとゆるふわなごや PDF
PDF
PDF
PPTX
PDF
x64 のスカラー,SIMD 演算性能を測ってみた @ C++ MIX #10 PDF
PDF
x64 のスカラー,SIMD 演算性能を測ってみた v0.1 @ C++ MIX #10 PDF
Intro to SVE 富岳のA64FXを触ってみた PDF
PPTX
PDF
PDF
PDF
Intel AVX-512/富岳SVE用SIMDコード生成ライブラリsimdgen PDF
PDF
PDF
PDF
Adding simpl GVN path into GHC PDF
More from MITSUNARI Shigeo
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
深層学習フレームワークにおけるIntel CPU/富岳向け最適化法 PDF
PDF
PDF
Lifted-ElGamal暗号を用いた任意関数演算の二者間秘密計算プロトコルのmaliciousモデルにおける効率化 PDF
PDF
PDF
PDF
ElGamal型暗号文に対する任意関数演算・再暗号化の二者間秘密計算プロトコルとその応用 Haswellサーベイと有限体クラスの紹介
- 1.
- 2.
- 3.
新機能
AVX2
256bit整数演算
FMA(Fused Multiply-Add)
積和演算
ビット演算、整数演算命令
TSX
最大8 u-op/cycleディスパッチ
L1 data, L2バンド幅の改良
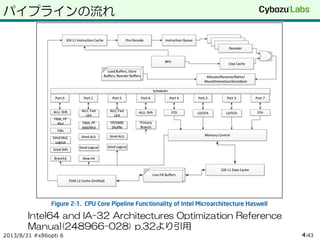
2013/8/31 #x86opti 6 /433
- 4.
- 5.
フロントエンド
In order(入った順序で)処理する部分
命令のフェッチとデコード
u-opキャッシュ(デコード済みIcache)
最大4個のデコード(複雑なものx1 単純なものx3)
このあたりはSandyとあまり変わらず
allocationキュー(最大56 u-op)
HTが有効なら2個の論理CPUで共有
Sandyは28 u-opの複製
片方がidleならもう片方が連続利用可能
2013/8/31 #x86opti 6 /435
- 6.
実行エンジン
リネーマ
ReOrderバッファは192個(Sandyは168個)
u-opキューからスケジューラにdispatch
Zero-idiom, one-idiomはここで行われてる
xor eax, eaxやcmpeq xm1, xm1などの処理
Zero-latency mov(Ivyから)
同じサイズのreg, xmm, ymm間のmov,
reg8からreg32/64へのmovzはここで行われる
スケジューラ
RS(reservation station)は60個(Sandyは54個)
8個のport(Sandyは6個)
168個のPRF(Physical Register FIle)
データを転送しない方式のレジスタファイル
2013/8/31 #x86opti 6 /436
- 7.
実行エンジン
実行コア
port0 ... port 7
演算系 x 4, メモリ系 x 4
FMAは2port(port 0, port 1)
double 8 x 2 op/cycle
SSEの整数と小数の扱いが別
同じxmmレジスタでも整数命令を実行したあと浮動小数点数命令
を実行すると1clkの遅延が発生
SSE-INT SSE-FP
AVX-INT AVX-FP
2013/8/31 #x86opti 6 /437
- 8.
キャッシュ
L1data(32KB/8way)の改良
load64byte/cycle(Sandyは32)
store 32byte/cycle(Sandyは16)
ymm(=32byte) 2入力1出力に対応
L2 TLBでラージページサポート
仮想アドレスから物理アドレスへの変換キャッシュ
Sandy ; 4KiB page x 512 = 2MiB
Haswell : 2MiB page x 1024 = 2GiB
2013/8/31 #x86opti 6 /438
- 9.
AVX2
Sandy, IvyのAVXは小数用
整数命令は全然変わらなかった
今回ようやく使えるようになった
大抵の256bit演算命令は上位128bitと下位128bitは相互作
用しない
256bit全体に影響する命令
vinsertf128, vinserti128, vextractf128など
一部への挿入、抽出
vpermd, vperm2f128などのシャッフル系
32bit x 8の行き先を自由に指定可能
vbroadcst, vpbroadcast系
最下位エレメントの値を全体にコピー
2013/8/31 #x86opti 6 /439
- 10.
FMA
𝑤 =±(𝑥 × 𝑦) ± 𝑧
𝑥 × 𝑦の時点で丸めは行われない
float x 32/cycle, double x 16/cycle ; 5 latency
アセンブラ表記
引数の順序を示す1, 2, 3を命令の末尾につける
i番目とj番目をかけてk番目の値を足す
vfmadd132pd, vfmadd213pd, vfmadd231pdとかある
2013/8/31 #x86opti 6 /4310
vfmadd𝑖𝑗𝑘 𝑝𝑑 𝑥1 𝑥2 𝑥3 ; 𝑥1= 𝑥𝑖× 𝑥𝑗 + 𝑥 𝑘
- 11.
(例)ベクトルの内積を求める
(注意)これだとlatencyは隠蔽できない(1clk/loop)
gcc4.8は単純ループで自動的にFMA命令を生成
2013/8/31#x86opti 6 /4311
// double dot(const double *px, const double *py, size_t n);
...
vxorpd(ym0, ym0);
L("@@");
vmovapd(ym1, ptr[px + n * 8]);
// ym0 += ym1 * py[n]
vfmadd231pd(ym0, ym1, ptr[py + n * 8]);
add(n, 4);
jnz("@b");
vhaddpd(ym0, ym0); // [d:c:b:a] => [*:d+c:*:b+a]
vpermpd(ym0, ym0, 1 << 3); [*:*:d+c:b+a]
vhaddpd(ym0, ym0); [*:*:* :a+b+c+d]
ret();
- 12.
- 13.
load/store
SSEは16byteアラインされていることが望ましい
Nehalem以降アラインされていなくてもmovupsなどは速い
AVX2では32byteアラインが望ましい
loadかstoreのどちからだけアライン可能ならstoreを優先
16byte x 2の読み書きに分割する
2013/8/31 #x86opti 6 /4313
vmovups ym0, [mem] // 32byte load
vmovups xm0, [mem] // 下位16byte load
vinsertf128 ym0, ym0, [mem + 16], 1 // 上位16byte load
vmovups [mem], ym0 // 32byte store
vmovups [mem], xm0 // 下位16byte store
vextractf128 [mem + 16], ym0, 1 // 上位16byte store
- 14.
進化したrep movsb
memcpy
SIMDを使う
非アライン、ループの端数処理がめんどい
rep movsb(n<=3) + rep movsd(4の倍数)
Ivy以降rep movsbがかなり速くなってる
ERMSB(Enhanced Rep Movsb)
アライメントの処理不要
端数処理不要
バイトコードはrep movsbと同じだが速度が違う
eax=7, ecx=0でcpuidしたebxの9ビット目が1なら使える
2013/8/31 #x86opti 6 /4314
- 15.
rep_movsb vs SIMD
実験コード(ちょー簡単)
AVX2版(手抜き)
2013/8/31 #x86opti 6 /4315
// void (void *dst, const void *src, size_t n);
mov rcx, rdx
rep_movsb // 0xf3, 0xa4
ret
L("@@");
vmovaps(ym0, ptr [src]);
vmovaps(ym1, ptr [src + 32]);
vmovaps(ptr [dst], ym0);
vmovaps(ptr [dst + 32], ym1);
add(src, 64);
add(dst, 64);
sub(n, 64);
jnz("@b");
- 16.
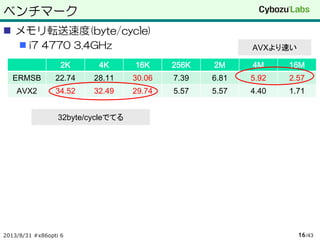
ベンチマーク
2K 4K 16K256K 2M 4M 16M
ERMSB 22.74 28.11 30.06 7.39 6.81 5.92 2.57
AVX2 34.52 32.49 29.74 5.57 5.57 4.40 1.71
2013/8/31 #x86opti 6 /4316
メモリ転送速度(byte/cycle)
i7 4770 3.4GHz
32byte/cycleでてる
AVXより速い
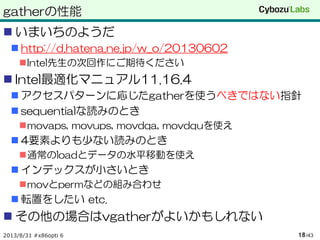
- 17.
gather
インデックスで指定された場所のメモリをそれぞれ
読んできて一つのレジスタに入れる
例: 32bitのインデックスを使ってdoubleを読む
xm2[i] : 各要素のインデックス
ym3[i] : MSBが1なら読み込む, 0なら0を設定する
2013/8/31 #x86opti 6 /4317
vgatherqpd ym1, [rax + xm2 * 4], ym3
// 擬似コード
for (int i = 0; i < 4; i++) {
if (ym3[i] & (1<<63)) {
ym1[i] = *(double *)(rax + xm2[i] * 4);
} else {
ym1[i] = 0;
}
}
- 18.
- 19.
Haswellで追加されたビット操作命令
3op形式
VEXエンコード.86モードでは利用できない
BMI1命令群
andn, bextr, blsi, blsmsk, blsr, tzcnt
BMI2命令群
bzhi, mulx, pdep, pext, rorx, sarx, shlx, shrx
利用可能かの判別方法
eax = 7, ecx = 0でcpuidを呼び出す
ebxの3bit目(BMI1)と8ビット目(BMI2)
lzcnt(≒bsr)だけeax = 0のcpuidの結果のecx の5bit目
2013/8/31 #x86opti 6 /4319
- 20.
BMI1命令群
主にビットマスク系
andn(x,y) = ~x & y
bextr(x, start | (len << 8))
xの[start+len-1:start]のビットを取り出す(範囲外は0拡張)
blsi(x) = x & (-x)
blsmsk(x) = x ^ (x-1)
blsr(x) = x & (x-1)
tzcnt(入力0のとき0になることを除いてbsfと同じ)
bzhi(x, n) = x & (~((-1) << n))
bzhi(x, n) = bextr(x, n << 8)
bzhiでよいときはbzhiのほうが速いようだ
2013/8/31 #x86opti 6 /4320
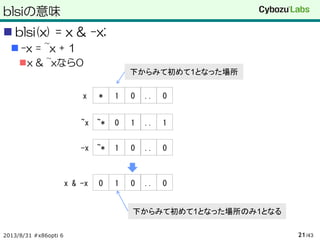
- 21.
blsiの意味
blsi(x) =x & -x;
-x = ~x + 1
x & ~xなら0
2013/8/31 #x86opti 6 /4321
下からみて初めて1となった場所
1..10~*~x
0..01*x
0..01~*-x
0..010x & -x
下からみて初めて1となった場所のみ1となる
- 22.
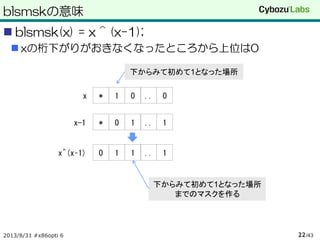
blsmskの意味
blsmsk(x) =x ^ (x-1);
xの桁下がりがおきなくなったところから上位は0
2013/8/31 #x86opti 6 /4322
下からみて初めて1となった場所
1..10*x-1
0..01*x
1..110x^(x–1)
下からみて初めて1となった場所
までのマスクを作る
- 23.
blsrの意味
blsr(x) =x & (x-1);
xの桁下がりがおきなくなったところまで消える
2013/8/31 #x86opti 6 /4323
下からみて初めて1となった場所
1..10*x-1
0..01*x
0..00*x&(x–1)
下からみて初めて1となった場所
までを0クリアする
- 24.
BMI2命令群
マスクやビットのコピーや取り出し
bzhi(x,y, n)
nbitより上をクリア ; x = y & ~((1 << n) - 1)
pdep(x, y, m)
マスクmに応じてyのbitを
xにコピー
pext(x, y, m)
マスクmに応じてyのbitを
縮約
2013/8/31 #x86opti 6 /4324
00110011m
00110011m
00y0y100y2y3x
y0y1y2y3y
y0y1y2y3y4y5y6y7y
y2y3y6y7x
- 25.
- 26.
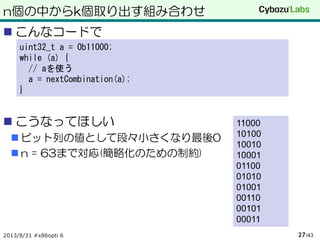
n個の中からk個取り出す組み合わせ
n個の中からk個取りだず組み合わせの列を生成
next_permutationは次に
小さいパターンを返す
一番小さくなったあとは0で終了
これをビット演算でしよう
2013/8/31 #x86opti 6 /4326
std::vector<bool> v(n);
std::fill(v.begin() + n - k, v.end(), true);
do {
// v[i] == trueとなるi
} while (std::next_permutation(v.begin(), v.end()));
例 n = 5, k = 2のとき
0 1 2 3 4
0 0 0 1 1 | 3 4
0 0 1 0 1 | 2 4
0 0 1 1 0 | 2 3
0 1 0 0 1 | 1 4
0 1 0 1 0 | 1 3
0 1 1 0 0 | 1 2
1 0 0 0 1 | 0 4
1 0 0 1 0 | 0 3
1 0 1 0 0 | 0 2
1 1 0 0 0 | 0 1
- 27.
n個の中からk個取り出す組み合わせ
こんなコードで
こうなってほしい
ビット列の値として段々小さくなり最後0
n = 63まで対応(簡略化のための制約)
2013/8/31 #x86opti 6 /4327
uint32_t a = 0b11000;
while (a) {
// aを使う
a = nextCombination(a);
}
11000
10100
10010
10001
01100
01010
01001
00110
00101
00011
- 28.
- 29.
aが奇数のとき
数の変化
b= (a + 1) ^ aでs個の1になる
その値の半分を引くと下位sビットがクリアされる
c = a – b/2
cから1 << (t-1)を引きたい
c & -cで1 << (t+s)ができる
s = bsr(b + 1) - 1
2013/8/31 #x86opti 6 /4329
* 1 0...0 1...1 ; [1個の1, t個の0, s個の1] ; 奇数の一般形
↓
* 0 1...1 0...0 ; [1個の0, s個の1, (t-1)個の0]
a = * 1 0...0 1...1 ; [1個の1, t個の0, s個の1]
↓
c = * 1 0...0 0...0 ; [1個の1, (t+s)個の0]
- 30.
nextCombinationC
gcc-4.8.1では自動的にblsi, lznctなどの命令を利用
2013/8/31#x86opti 6 /4330
size_t nextCombinationC(size_t a) {
if (a & 1) {
size_t b = a ^ (a + 1);
size_t c = a - b / 2;
return c - ((c & -c) >> bsr(b + 1));
} else {
return a - (a & -a) / 2;
} }
// コードの一部
lea rdx, [rdi+1]
xor rdx, rdi
mov rax, rdx
add rdx, 1
shr rax
lzcnt rdx, rdx
- 31.
intrinsic
includeファイル
VCはintrin.h
gccは-mbmi, -mbmi2つきでx86intrin.h
intrinsicが一部違う?
たとえばbextrはIntelのマニュアルでは
_bextr_u32(src, start, len);
gccでは__bextr_u32(src, start | (len << 8));
BMI1系の他の命令もgccでは二重アンダースコア
従来のintrinsicやBMI2系はアンダースコアが1個
適当にラップする(面倒)
rorxなどは従来のCのコードでもOK
2013/8/31 #x86opti 6 /4331
uint32_t rotl32(uint32_t x, int8_t r) { return (x << r) | (x >> (32 - r)); }
rotl32(x, 3); → // rorx ecx, eax, 29
- 32.
- 33.
mulx
フラグを変更しない乗算命令
出力先を自由に設定できる(従来は[rdx:rax]固定)
前回の勉強会で紹介。今回は実際に使ってみた
従来の多倍長乗算コード
(例:256bit x 64bit)
mulを先に4回する
CFを壊さないようにするため
4 * 2 = 8個の値を保持する必要がある
そのあと連続してaddを実行
2013/8/31 #x86opti 6 /4333
mulx x, y, z ; [x:y] <= z * rdx
mov(rax, ptr [py]);
mul(x);
mov(t0, rax);
mov(t1, rdx);
mov(rax, ptr [py + 8]);
mul(x);
mov(t, rax);
mov(t2, rdx);
mov(rax, ptr [py + 8 * 2]);
mul(x);
mov(t3, rax);
mov(rax, x);
mov(x, rdx);
mul(qword [py + 8 * 3]);
add(t1, t);
adc(t2, t3);
adc(x, rax);
adc(rdx, 0);
- 34.
mulxを使った乗算
mulxとaddを混ぜて利用できる
テンポラリな値を保持する必要がない
不要なmov命令の削減
必要なレジスタの削減
2013/8/31 #x86opti 6 /4334
// 入力 uint64_t x, py[4];
// 出力 [rdx:t2:t1:t0] ; 小文字は汎用レジスタ
mov(rdx, x);
mulx(t1, t0, ptr [py + 8 * 0]); // [t1:t0] = y[0] * x
mulx(t2, rax, ptr [py + 8 * 1]); // [t2:rax] = y[1] * x
add(t1, rax);
mulx(x, rax, ptr [py + 8 * 2]); // [x:rax] = y[2] * x
adc(t2, rax);
mulx(rdx, rax, ptr [py + 8 * 3]); // [rdx:rax] = y[3] * x
adc(x, rax);
adc(rdx, 0);
- 35.
pairingライブラリでの効果
128bitセキュリティのライブラリ
mulxなし1.13Mclk(0.333msec)@i7-4770 3.4GHz
mulxあり 1.01Mclk(0.298msec)
約12%の高速化
世界最速(多分)
see https://github.com/herumi/ate-pairing
TEPLA(筑波大学のCとGMPによる汎用ライブラリ)
http://www.cipher.risk.tsukuba.ac.jp/tepla/benchmark
.html
BN254(多分同じセキュリティレベル)が2.4msecだった
2013/8/31 #x86opti 6 /4335
- 36.
有限体Fp
pを素数としてFp ={0, 1, 2, ..., p-1}
この上の四則演算ができる(閉じている)
加減算、乗算は通常の計算のあとpで割った余りとする
a ± b := (a ± b) mod p
a * b := (a * b) mod p
例(p=13) 𝐹13 = {0, 1, 2, 3, ... 12 }
3 + 5 = 8
9 + 11 = 20 = 7 (mod 13)
3 * 5 = 15 = 2 (mod 13)
3 * 9 = 27 = 1 (mod 13)
3 * 9 = 1ということなので3の逆数(1 / 3)は9とする
割り算ができる
7 / 3 = 7 * (1/3) = 7 * 9 = 63 = 11 (mod 13)
2013/8/31 #x86opti 6 /4336
- 37.
Montgomery乗算
a *b mod pのmod pは結構重たい
pを特殊な形(決め打ち)にした高速なアルゴリズム
今回はpの形によらずに一般的にそれなりに速いものを
Montgomery乗算は通常の乗算と剰余を同時に行う
p:素数, R := (1 << (pのビット長)) % p
mont(x, y) := x * y / R
この計算は比較的高速に実行できることが知られている
mont(xR, yR) = xyR^2 / R = xyR
これは通常世界のx * y xRの世界のmont(xR, yR)を意味する
一度RをかけてxRの世界にいれば
加減算はそのまま
乗算はmulがmontになる世界
除算はちょっと遅くなる(多分)
2013/8/31 #x86opti 6 /4337
- 38.
有限体クラスライブラリ
mie::MontFpTテンプレートクラス(開発中)
前述のライブラリの一部を取り出して新しく作り直したもの
特長
ビット長と、素数の文字列をsetModuloに指定すると、その
素数に応じたMontgomery乗算を実行時生成するクラス
ただし現状はpのビットパターンに応じた最適化はしていない
今回は192ビット~256ビットぐらいの素数を対象
コード上は576ビットまで対応してるが除算がまだ速くない
ビット長が小さいのでRSA向けではない(別の暗号用途)
実装
https://github.com/herumi/mie/blob/master/include/
mie/mont_fp.hpp
要 –lgmp, -lgmpxx
2013/8/31 #x86opti 6 /4338
- 39.
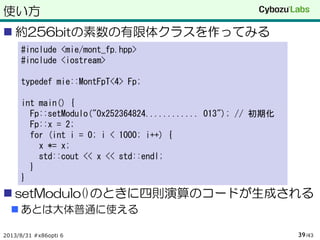
使い方
約256bitの素数の有限体クラスを作ってみる
setModulo()のときに四則演算のコードが生成される
あとは大体普通に使える
2013/8/31 #x86opti 6 /4339
#include <mie/mont_fp.hpp>
#include <iostream>
typedef mie::MontFpT<4> Fp;
int main() {
Fp::setModulo("0x252364824............ 013"); // 初期化
Fp::x = 2;
for (int i = 0; i < 1000; i++) {
x *= x;
std::cout << x << std::endl;
}
}
- 40.
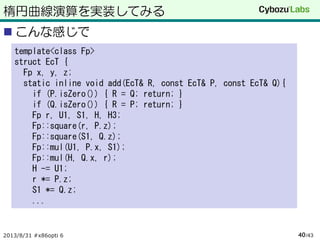
楕円曲線演算を実装してみる
こんな感じで
2013/8/31 #x86opti6 /4340
template<class Fp>
struct EcT {
Fp x, y, z;
static inline void add(EcT& R, const EcT& P, const EcT& Q){
if (P.isZero()) { R = Q; return; }
if (Q.isZero()) { R = P; return; }
Fp r, U1, S1, H, H3;
Fp::square(r, P.z);
Fp::square(S1, Q.z);
Fp::mul(U1, P.x, S1);
Fp::mul(H, Q.x, r);
H -= U1;
r *= P.z;
S1 *= Q.z;
...
- 41.
細かい注意
通常の数値と内部表現の変換に一度montを呼ぶ
同じ定数を何度も使うなら一度変数に入れた方が速い
内部のバイナリ表現が元の値の順序を保持しない
そのため比較命令<, >, <=, >=を持っていない
ゼロとの比較は可能(isZero())
異なるpに対するMontFpTは異なる型
MontFpT<3>とMontFpT<4>には何の関係もない
同じMontFpT<3>で異なるpを使いたいときはtagを指定する
setModulo()はスレッドセーフではない
通常一度だけ設定することを想定している
2013/8/31 #x86opti 6 /4341
for (;;) x *= 2; // 毎回(int)2 => Fp(2)の変換が走る
Fp::two = 2; for (;;) x *= two; // 変換は一度ですむ
- 42.
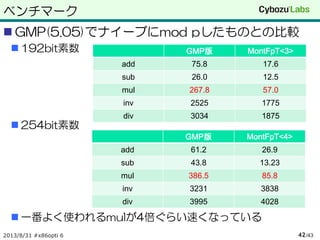
ベンチマーク
GMP(5.05)でナイーブにmod pしたものとの比較
192bit素数
254bit素数
一番よく使われるmulが4倍ぐらい速くなっている
2013/8/31 #x86opti 6 /4342
GMP版 MontFpT<3>
add 75.8 17.6
sub 26.0 12.5
mul 267.8 57.0
inv 2525 1775
div 3034 1875
GMP版 MontFpT<4>
add 61.2 26.9
sub 43.8 13.23
mul 386.5 85.8
inv 3231 3838
div 3995 4028
- 43.
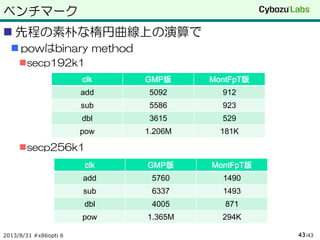
ベンチマーク
先程の素朴な楕円曲線上の演算で
powはbinarymethod
secp192k1
secp256k1
2013/8/31 #x86opti 6 /4343
clk GMP版 MontFpT版
add 5092 912
sub 5586 923
dbl 3615 529
pow 1.206M 181K
clk GMP版 MontFpT版
add 5760 1490
sub 6337 1493
dbl 4005 871
pow 1.365M 294K









![(例)ベクトルの内積を求める
(注意)これだとlatencyは隠蔽できない(1clk/loop)
gcc4.8は単純ループで自動的にFMA命令を生成
2013/8/31 #x86opti 6 /4311
// double dot(const double *px, const double *py, size_t n);
...
vxorpd(ym0, ym0);
L("@@");
vmovapd(ym1, ptr[px + n * 8]);
// ym0 += ym1 * py[n]
vfmadd231pd(ym0, ym1, ptr[py + n * 8]);
add(n, 4);
jnz("@b");
vhaddpd(ym0, ym0); // [d:c:b:a] => [*:d+c:*:b+a]
vpermpd(ym0, ym0, 1 << 3); [*:*:d+c:b+a]
vhaddpd(ym0, ym0); [*:*:* :a+b+c+d]
ret();](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-11-320.jpg)
![cf. 4次のベクトルの内積
dppsやdppdを使えばよい(SSE4.1から)
2013/8/31 #x86opti 6 /4312
xa = [a3:a2:a1:a0]
xb = [b3:b2:b1:b0]
dpps xa, xb, 0xf1 ; [0:0:0:a0*b0+a1*b1+a2*b2+a3*b3]](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-12-320.jpg)
![load/store
SSEは16byteアラインされていることが望ましい
Nehalem以降アラインされていなくてもmovupsなどは速い
AVX2では32byteアラインが望ましい
loadかstoreのどちからだけアライン可能ならstoreを優先
16byte x 2の読み書きに分割する
2013/8/31 #x86opti 6 /4313
vmovups ym0, [mem] // 32byte load
vmovups xm0, [mem] // 下位16byte load
vinsertf128 ym0, ym0, [mem + 16], 1 // 上位16byte load
vmovups [mem], ym0 // 32byte store
vmovups [mem], xm0 // 下位16byte store
vextractf128 [mem + 16], ym0, 1 // 上位16byte store](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-13-320.jpg)

![rep_movsb vs SIMD
実験コード(ちょー簡単)
AVX2版(手抜き)
2013/8/31 #x86opti 6 /4315
// void (void *dst, const void *src, size_t n);
mov rcx, rdx
rep_movsb // 0xf3, 0xa4
ret
L("@@");
vmovaps(ym0, ptr [src]);
vmovaps(ym1, ptr [src + 32]);
vmovaps(ptr [dst], ym0);
vmovaps(ptr [dst + 32], ym1);
add(src, 64);
add(dst, 64);
sub(n, 64);
jnz("@b");](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-15-320.jpg)
![gather
インデックスで指定された場所のメモリをそれぞれ
読んできて一つのレジスタに入れる
例 : 32bitのインデックスを使ってdoubleを読む
xm2[i] : 各要素のインデックス
ym3[i] : MSBが1なら読み込む, 0なら0を設定する
2013/8/31 #x86opti 6 /4317
vgatherqpd ym1, [rax + xm2 * 4], ym3
// 擬似コード
for (int i = 0; i < 4; i++) {
if (ym3[i] & (1<<63)) {
ym1[i] = *(double *)(rax + xm2[i] * 4);
} else {
ym1[i] = 0;
}
}](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-17-320.jpg)

![BMI1命令群
主にビットマスク系
andn(x, y) = ~x & y
bextr(x, start | (len << 8))
xの[start+len-1:start]のビットを取り出す(範囲外は0拡張)
blsi(x) = x & (-x)
blsmsk(x) = x ^ (x-1)
blsr(x) = x & (x-1)
tzcnt(入力0のとき0になることを除いてbsfと同じ)
bzhi(x, n) = x & (~((-1) << n))
bzhi(x, n) = bextr(x, n << 8)
bzhiでよいときはbzhiのほうが速いようだ
2013/8/31 #x86opti 6 /4320](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-20-320.jpg)



![n個の中からk個取り出す組み合わせ
n個の中からk個取りだず組み合わせの列を生成
next_permutationは次に
小さいパターンを返す
一番小さくなったあとは0で終了
これをビット演算でしよう
2013/8/31 #x86opti 6 /4326
std::vector<bool> v(n);
std::fill(v.begin() + n - k, v.end(), true);
do {
// v[i] == trueとなるi
} while (std::next_permutation(v.begin(), v.end()));
例 n = 5, k = 2のとき
0 1 2 3 4
0 0 0 1 1 | 3 4
0 0 1 0 1 | 2 4
0 0 1 1 0 | 2 3
0 1 0 0 1 | 1 4
0 1 0 1 0 | 1 3
0 1 1 0 0 | 1 2
1 0 0 0 1 | 0 4
1 0 0 1 0 | 0 3
1 0 1 0 0 | 0 2
1 1 0 0 0 | 0 1](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-26-320.jpg)

![aが奇数のとき
数の変化
b = (a + 1) ^ aでs個の1になる
その値の半分を引くと下位sビットがクリアされる
c = a – b/2
cから1 << (t-1)を引きたい
c & -cで1 << (t+s)ができる
s = bsr(b + 1) - 1
2013/8/31 #x86opti 6 /4329
* 1 0...0 1...1 ; [1個の1, t個の0, s個の1] ; 奇数の一般形
↓
* 0 1...1 0...0 ; [1個の0, s個の1, (t-1)個の0]
a = * 1 0...0 1...1 ; [1個の1, t個の0, s個の1]
↓
c = * 1 0...0 0...0 ; [1個の1, (t+s)個の0]](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-29-320.jpg)
![nextCombinationC
gcc-4.8.1では自動的にblsi, lznctなどの命令を利用
2013/8/31 #x86opti 6 /4330
size_t nextCombinationC(size_t a) {
if (a & 1) {
size_t b = a ^ (a + 1);
size_t c = a - b / 2;
return c - ((c & -c) >> bsr(b + 1));
} else {
return a - (a & -a) / 2;
} }
// コードの一部
lea rdx, [rdi+1]
xor rdx, rdi
mov rax, rdx
add rdx, 1
shr rax
lzcnt rdx, rdx](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-30-320.jpg)


![mulx
フラグを変更しない乗算命令
出力先を自由に設定できる(従来は[rdx:rax]固定)
前回の勉強会で紹介。今回は実際に使ってみた
従来の多倍長乗算コード
(例:256bit x 64bit)
mulを先に4回する
CFを壊さないようにするため
4 * 2 = 8個の値を保持する必要がある
そのあと連続してaddを実行
2013/8/31 #x86opti 6 /4333
mulx x, y, z ; [x:y] <= z * rdx
mov(rax, ptr [py]);
mul(x);
mov(t0, rax);
mov(t1, rdx);
mov(rax, ptr [py + 8]);
mul(x);
mov(t, rax);
mov(t2, rdx);
mov(rax, ptr [py + 8 * 2]);
mul(x);
mov(t3, rax);
mov(rax, x);
mov(x, rdx);
mul(qword [py + 8 * 3]);
add(t1, t);
adc(t2, t3);
adc(x, rax);
adc(rdx, 0);](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-33-320.jpg)
![mulxを使った乗算
mulxとaddを混ぜて利用できる
テンポラリな値を保持する必要がない
不要なmov命令の削減
必要なレジスタの削減
2013/8/31 #x86opti 6 /4334
// 入力 uint64_t x, py[4];
// 出力 [rdx:t2:t1:t0] ; 小文字は汎用レジスタ
mov(rdx, x);
mulx(t1, t0, ptr [py + 8 * 0]); // [t1:t0] = y[0] * x
mulx(t2, rax, ptr [py + 8 * 1]); // [t2:rax] = y[1] * x
add(t1, rax);
mulx(x, rax, ptr [py + 8 * 2]); // [x:rax] = y[2] * x
adc(t2, rax);
mulx(rdx, rax, ptr [py + 8 * 3]); // [rdx:rax] = y[3] * x
adc(x, rax);
adc(rdx, 0);](https://image.slidesharecdn.com/x86opti6-130831171608-phpapp01/85/Haswell-34-320.jpg)