Download as PDF, PPTX
![• 紛失通信OT(Oblivious Transfer)
• https://ppdm.jp/ot/
• 円周率のN桁(1<N<100万)をNを隠して問い合わせる
• https://ppdm.jp/ot/
• クライアント𝐸𝑛𝑐(𝑚)
• サーバ𝑇𝑎𝑏𝑙𝑒 𝐸𝑛𝑐 𝑚 = 𝐸𝑛𝑐[𝑇𝑎𝑏𝑙𝑒 𝑚 ]を返す
• FHEの例(京都大学の松岡-伴野-松本さん)
• FHEを使って動作するCPUとCコンパイラ開発セット
• https://virtualsecureplatform.github.io/
L2HE, FHEを使ったデモ
4 / 18](https://image.slidesharecdn.com/anninbon11-211209091259/85/11-4-320.jpg)
Uploaded byMITSUNARI Shigeo
暗認本読書会11
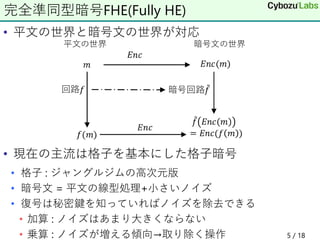
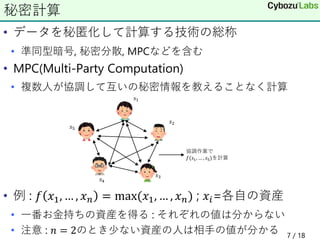
The document summarizes key concepts in homomorphic encryption and secure multiparty computation including: 1) Homomorphic encryption allows computations to be performed directly on encrypted data without decrypting it first, such as adding or multiplying encrypted values. 2) Secure multiparty computation allows multiple parties to jointly compute a function over their private inputs while keeping those inputs private. 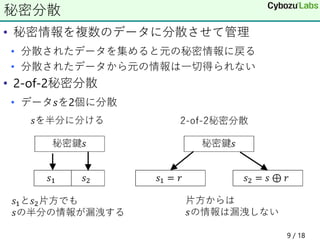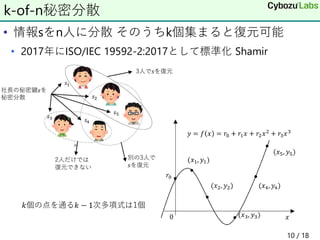3) Secret sharing techniques like Shamir's secret sharing and verifiable secret sharing (VSS) allow a secret to be divided into shares and reconstructed from a subset of shares.
More Related Content
暗認本読書会11
- 1. 暗認本読書会11 準同型暗号, MPC, 秘密分散,DKG, ペアリング, BLS署名 2021/12/9 https://anninbon.connpass.com/ 光成滋生
- 2. • 暗号文のまま復号せずに計算する暗号技術 • 暗号文同士の足し算: 𝐸𝑛𝑐 𝑚1 + 𝐸𝑛𝑐 𝑚2 = 𝐸𝑛𝑐 𝑚1 + 𝑚2 • 暗号文同士の掛け算 : 𝐸𝑛𝑐 𝑚1 × 𝐸𝑛𝑐 𝑚2 = 𝐸𝑛𝑐(𝑚1𝑚2) • コンピュータの計算 • ビット演算andとxor(排他的論理和)で全ての回路は作れる • 𝔽2 = {0,1}の足し算 • 0 + 0 = 0, 0 + 1 = 1 + 0 = 1, 1 + 1 = 0 ; これはxor • 0 × 0 = 1 × 0 = 0 × 1 = 0, 1 × 1 = 1 ; これはand • 1bit暗号文の足し算と掛け算→任意の計算が可能 • 掛け算のみ、足し算のみは昔から知られていた • 両方出来るものの構成が長らくの未解決問題 • 2009年Gentryが構築→完全準同型暗号の発展 準同型暗号HE(Homomorphic Encryption) 2 / 18
- 3. • 画像のエッジ検出(AHE) • クライアントで撮った2値画像を暗号化してサーバに送信 •サーバでエッジ強調処理をしてクライアントに渡して復号 • https://github.com/herumi/ahe-demo • クロス集計(WebAssemblyで実装) • https://herumi.github.io/she-wasm/ デモ 3 / 18
- 4. • 紛失通信OT(Oblivious Transfer) •https://ppdm.jp/ot/ • 円周率のN桁(1<N<100万)をNを隠して問い合わせる • https://ppdm.jp/ot/ • クライアント𝐸𝑛𝑐(𝑚) • サーバ𝑇𝑎𝑏𝑙𝑒 𝐸𝑛𝑐 𝑚 = 𝐸𝑛𝑐[𝑇𝑎𝑏𝑙𝑒 𝑚 ]を返す • FHEの例(京都大学の松岡-伴野-松本さん) • FHEを使って動作するCPUとCコンパイラ開発セット • https://virtualsecureplatform.github.io/ L2HE, FHEを使ったデモ 4 / 18
- 5. • 平文の世界と暗号文の世界が対応 • 現在の主流は格子を基本にした格子暗号 •格子 : ジャングルジムの高次元版 • 暗号文 = 平文の線型処理+小さいノイズ • 復号は秘密鍵を知っていればノイズを除去できる • 加算 : ノイズはあまり大きくならない • 乗算 : ノイズが増える傾向→取り除く操作 完全準同型暗号FHE(Fully HE) 5 / 18
- 6. • 乗算回数の上限で分類 • 加法準同型暗号AHEで出来ること •𝐸𝑛𝑐 𝑥 + 𝐸𝑛𝑐 𝑥 = 𝐸𝑛𝑐 𝑥 + 𝑥 = 𝐸𝑛𝑐 2𝑥 • 𝐸𝑛𝑐 2𝑥 + 𝐸𝑛𝑐 𝑥 = 𝐸𝑛𝑐 2𝑥 + 𝑥 = 𝐸𝑛𝑐 3𝑥 • 一般に暗号文の𝑛倍𝑛𝐸𝑛𝑐 𝑥 = 𝐸𝑛𝑐(𝑛𝑥)は計算可能 • 2レベル準同型暗号2LHEで出来ること • 2個のベクトルデータ𝑥 = (𝑥1, … , 𝑥𝑛)と𝑦 = (𝑦1, … , 𝑦𝑛)の内積 • 𝐸𝑛𝑐 𝑥1 , … , 𝐸𝑛𝑐 𝑥𝑛 ⋅ 𝐸𝑛𝑐 𝑦1 , … , 𝐸𝑛𝑐 𝑦𝑛 = 𝐸𝑛𝑐 ∑𝑥𝑖𝑦𝑖 • 平均, 標準偏差, 2個のベクトルのcos類似度など 準同型暗号のレベル 準同型暗号の種類 加算 乗算 演算コスト 加法準同型暗号 任意回 0 軽い 2レベル準同型暗号 任意回 1 まあまあ Nレベル準同型暗号 任意回 N-1 Nが大きいほど重たい 完全準同型暗号 任意回 任意回 重たい 6 / 18
- 7. • データを秘匿化して計算する技術の総称 • 準同型暗号,秘密分散, MPCなどを含む • MPC(Multi-Party Computation) • 複数人が協調して互いの秘密情報を教えることなく計算 • 例 : 𝑓 𝑥1, … , 𝑥𝑛 = max(𝑥1, … , 𝑥𝑛) ; 𝑥𝑖=各自の資産 • 一番お金持ちの資産を得る : それぞれの値は分からない • 注意 : 𝑛 = 2のとき少ない資産の人は相手の値が分かる 秘密計算 7 / 18
- 8. • semi-honestモデル • プロトコルの参加者はプロトコルに正しく従う •計算途中に取得した値から精一杯相手の情報は得ろうとする • maliciousモデル • プロトコルに従わない • 自分に有利な情報を得たら途中で止める • 一貫性の無い値を提出する • 注意 : 一貫して嘘の値を付くのは対象外(資産の嘘の報告) • 一般に • semi-honestモデルの方が効率がよい • maliciousモデルでは嘘つきが参加者のうちどれぐらいいるか によって効率やプロトコルが変わる • ブロックチェーンなど不特定多数の参加者 モデル 8 / 18
- 9. • 秘密情報を複数のデータに分散させて管理 • 分散されたデータを集めると元の秘密情報に戻る •分散されたデータから元の情報は一切得られない • 2-of-2秘密分散 • データ𝑠を2個に分散 秘密分散 9 / 18
- 10. • 情報sをn人に分散 そのうちk個集まると復元可能 •2017年にISO/IEC 19592-2:2017として標準化 Shamir k-of-n秘密分散 𝑘個の点を通る𝑘 − 1次多項式は1個 10 / 18
- 11. • 秘密分散の問題点 • 秘密分散で社長がある人にだけ嘘の値を教えていたら •その人は復元できない • 正しい値をもらったか確認するには集まらなければならない • VSS (Feldman) • 検証可能な秘密分散 • 秘密鍵𝑠を𝑠1, … , 𝑠𝑛に秘密分散 • 楕円曲線の点Pを公開𝑠𝑃, 𝑠1𝑃, … , 𝑠𝑛𝑃も公開 • 各自は秘密鍵𝑠𝑖と𝑠𝑖𝑃の対応がとれていることを確認 • DLPの困難性により𝑠𝑖𝑃から𝑠𝑖は分からない • 𝑠1𝑃, … , 𝑠𝑛𝑃から𝑠𝑃を復元 : みなが同じ値を復元できたか確認 VSS (Verifiable Secret Sharing) 11 / 18
- 12. • 秘密分散は特定の人の秘密情報𝑠を分散 • 情報を持つ人が強い •DKG • 権力を分散する(MPCの一種) • それぞれがVSSを実行して自分の秘密情報を秘密分散 • 全員の秘密分散を集め, 秘密情報の和を全体の秘密情報とする • 安全性証明をつけるためにはもう少し複雑なプロトコル • ブロックチェーンなどの非中央集権的なネットワークで利用 DKG (Distributed Key Generation) 12 / 18
- 13. • 2個のベクトルの外積 • 𝑥= 𝑎, 𝑏 , 𝑦 = (𝑐, 𝑑)に対して𝑥 × 𝑦 = 𝑎𝑑 − 𝑏𝑐 • 楕円曲線 • トーラス(長方形の向かい合う辺をつけたもの) • 楕円曲線の点を2個の整数の組で表現 • 𝑃 = 𝑎𝑒1 + 𝑏𝑒2, 𝑄 = 𝑐𝑒1 + 𝑑𝑒2 • 𝑃と𝑄のペアリング𝑒(𝑃, 𝑄) • 点𝑃と𝑄の外積に相当するもの • 値は有限体の拡大体の元(詳細略) • 「𝑃 × 𝑄」と書くことにする(ここだけの記法) • 𝑛𝑃 × 𝑚𝑄 = 𝑛𝑚(𝑃 × 𝑄) ペアリング 𝑥 = (𝑎, 𝑏) 𝑦 = (𝑐, 𝑑) 𝑎𝑑 − 𝑏𝑐 (𝑎, 𝑏) (𝑐, 𝑑) 13 / 18
- 14. • ペアリングを使った署名 • 𝑃: 楕円曲線の点 • 𝐻 : 楕円曲線の点へのハッシュ関数 • 鍵生成 • 𝑠 : 署名鍵(秘密鍵), 𝑄 = 𝑠𝑃 : 検証鍵(公開鍵) • 署名 • 𝑚 : メッセージ, 𝜎 = 𝑠𝐻(𝑚) • 検証 • 与えられた(𝑚, 𝜎)に対して「𝐻 𝑚 × 𝑄 = 𝜎 × 𝑃」なら受理 • 正しければ𝐻 𝑚 × 𝑠𝑃 = 𝑠 𝐻 𝑚 × 𝑃 = 𝜎 × 𝑃 • 特長 • ECDSAと違って乱数不要 BLS署名 14 / 18
- 15. • 秘密分散と相性がよい • 検証鍵(公開鍵)が𝑠𝑃,署名が𝑠𝐻(𝑚)で どちらも「秘密鍵 x 楕円曲線の点」の形 • BLS署名を秘密分散と組み合わせると • 秘密分散と異なり(秘密鍵は秘密のままなので)繰り返し利用可 • ブロックチェーン系プロジェクトで利用 BLS署名の特長 15 / 18
- 16.
- 17. • 秘密情報𝑠の2-of-3秘密分散 • 乱数𝑠1,𝑠2を選び𝑠3 = 𝑠 − 𝑠1 − 𝑠2とする • A, B, Cにそれぞれ 𝑠1, 𝑠2 , 𝑠2, 𝑠3 , (𝑠3, 𝑠1)を渡す • 単独では𝑠は分からない • 二人集まると𝑠1, 𝑠2, 𝑠3が揃うので𝑠 = 𝑠1 + 𝑠2 + 𝑠3を復元可能 • 秘密分散のまま加算 • 秘密情報𝑠, 𝑡がA, B, Cに秘密分散されている • A : 𝑠1, 𝑠2 , 𝑡1, 𝑡2 • B : (𝑠2, 𝑠3), (𝑡2, 𝑡3) • C : (𝑠3, 𝑠1), (𝑡3, 𝑡1) • それぞれが分散された値のまま加算 • 𝐴 ∶ 𝑠1 + 𝑡1, 𝑠2 + 𝑡2 , 𝐵: 𝑠2 + 𝑡2, 𝑠3 + 𝑡3 , 𝐶 ∶ (𝑠3 + 𝑡3, 𝑠1 + 𝑡1) • これらは「𝑠 + 𝑡」の秘密分散となっている 3PCの例 17 / 18
- 18.