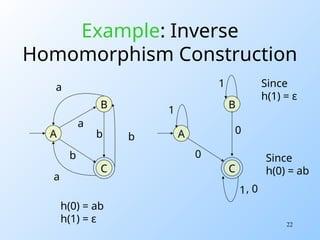
The document outlines the closure properties of regular languages, including operations like union, intersection, difference, concatenation, and reversal. It explains how to prove that these operations maintain regularity using finite automata and regular expressions. Examples are provided for each closure property, illustrating their applications and the corresponding proofs.





![6
Example: Product DFA for
Intersection
A
C
B
D
0
1
0, 1
1
1
0
0
[A,C] [A,D]
0
[B,C]
1
0
1
0
1
[B,D]
0
1](https://image.slidesharecdn.com/closurepropertiesofregularlanguages-241119063316-6328daad/85/Closure-Properties-of-Regular-Languages-ppt-6-320.jpg)

![8
Example: Product DFA for
Difference
A
C
B
D
0
1
0, 1
1
1
0
0
[A,C] [A,D]
0
[B,C]
1
0
1
0
1
[B,D]
0
1
Notice: difference
is the empty language](https://image.slidesharecdn.com/closurepropertiesofregularlanguages-241119063316-6328daad/85/Closure-Properties-of-Regular-Languages-ppt-8-320.jpg)