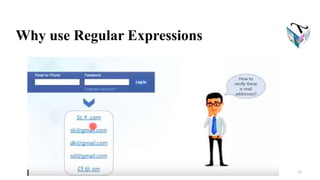
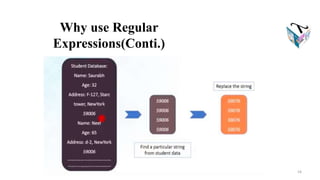
This document discusses regular expressions and provides examples. It begins by defining regular expressions recursively. Key points include: - Regular expressions can be used to concisely define languages. Common operations are concatenation, union, closure. - Examples show how regular expressions can define languages with certain properties like having a single 1 or an even number of characters. - Algebraic laws govern operations like distribution and idempotence for regular expressions. Concretization tests can verify proposed laws.

2. Lecture # 2
Advanced Theory Of Programming Languages
2

3. Agenda of lecture # 2
 Regular Expressions
 Recursive definition of Regular
Expression(RE)
 Why use Regular Expressions
 Regular Expressions: Different
languagesTypes
 RE Examples
3

4. Computational Model & Types, Computability Introduction to
languages, Pragmatics, Language Design Principles, Principle of
Programming Language Design, Syntax and Semantics, Types of
languages,Alphabets, Word, Defining Alphabets Guidline,Valid/In-
valid alphabets
4
Recall of Lecture-1

5. Regular Expressions
5

6. Defining Languages (Cont.)
Method of Regular Expressions
Consider the language L={Λ, x, xx, xxx,…} of strings, defined over Σ = {x}.
write this language as the Kleene star closure of alphabet Σ or L=Σ*
={x}*
this language can also be expressed by the regular expression x*
.
Similarly the language L={x, xx, xxx,…}, defined over Σ = {x}, can be expressed by the
regular expression x+.
6
6

7. Definition of a Regular Expression
• R is a regular expression if it is:
1. a for some a in the alphabet , standing for the language {a}
2. ε, standing for the language {ε}
3. Ø, standing for the empty language
4. R1+R2 where R1 and R2 are regular expressions, and + signifies union (sometimes |
is used)
5. R1R2 where R1 and R2 are regular expressions and this signifies concatenation
6. R* where R is a regular expression and signifies closure
7. (R) where R is a regular expression, then a parenthesized R is also a regular
expression
7

8. This definition may seem circular, but 1-3 form the basis Precedence: Parentheses have the
highest precedence, followed by *, concatenation, and then union.
Definition of a Regular Expression(Cont.)
8

9. Regular Expression
a*
generates Λ, a, aa, aaa, …
and a+
generates a, aa, aaa, aaaa, …, so the language L1 = {Λ, a, aa, aaa, …}
a
L2 = {a, aa, aaa, aaaa, …} can simply be expressed by a*
and a+
, respectively.
a*
and a+
are called the regular expressions (RE) for L1 and L2 respectively.
Note: a+
, aa*
and a*
a generate L2.
9
9

10. Regular Expression(conti)
– Now consider another language L, consisting of all possible strings,
defined over Σ = {a, b}. This language can also be expressed by the
regular expression
(a + b)*
.
– Now consider another language L, of strings having exactly double a,
defined over Σ = {a, b}, then it’s regular expression may be
b*
aab*
10

11. Example of Regular Expression(Conti.)
– Now consider another language L, of even length, defined over Σ = {a,
b}, then it’s regular expression may be
((a+b)(a+b))*
– Now consider another language L, of odd length, defined over Σ = {a,
b}, then it’s regular expression may be
(a+b)((a+b)(a+b))*
or
((a+b)(a+b))*
(a+b)
11

12. Recursive definition of Regular
Expression(RE)
Step 1: Every letter of Σ including Λ is a regular expression.
Step 2: If r1 and r2 are regular expressions then
1.(r1)
2.r1 r2
3.r1 + r2 and
4. r1
*
are also regular expressions.
Step 3: Nothing else is a regular expression.
12

13. Why use Regular Expressions
13

14. Why use Regular
Expressions(Conti.)
14

15. 15
Why use Regular Expressions(Conti.)

16. Why use Regular
Expressions(Conti.)
16

17. Regular Expressions: Different languages
17
https://regexr.com

18. RE Examples
• L(001) = {001}
• L(0+10*) = { 0, 1, 10, 100, 1000, 10000, … }
• L(0*10*) = {1, 01, 10, 010, 0010, …} i.e. {w | w has exactly a single 1}
• L()* = {w | w is a string of even length}
• L((0(0+1))*) = { ε, 00, 01, 0000, 0001, 0100, 0101, …}
• L((0+ε)(1+ ε)) = {ε, 0, 1, 01}
• L(1Ø) = Ø ; concatenating the empty set to any set yields the empty set.
• Rε = R
• R+Ø = R
• Note that R+ε may or may not equal R (we are adding ε to the language)
• Note that RØ will only equal R if R itself is the empty set.
18

19. Algebra for RE’s
• Commutative law for union:
L + M = M + L
• Associative law for union:
(L + M) + N = L + (M + N)
• Associative law for concatenation:
(LM)N = L(MN)
• Note that there is no commutative law for concatenation, i.e.
LM  ML
19

20. Algebra for RE’s (Conti.)
• The identity for union is:
L + Ø = Ø + L = L
• The identity for concatenation is:
Lε = εL = L
• The annihilator for concatenation is:
ØL = LØ = Ø
• Left distributive law:
L(M + N) = LM + LN
• Right distributive law:
M + N)L = LM + LN
• Idempotent law: 20

21. Laws Involving Closure
• (L*)* = L*
closing an already closed expression does not change
the language
• Ø* = ε
• ε* = ε
• L+ = LL* = L*L
more of a definition than a law
• L* = L+ + ε
• L? = ε + L
more of a definition than a law
21

22. Concretization Test
• For example
(R + S)* = (R*S*)*
We can substitute 0 for R and 1 for S.
The left side is clearly any sequence of 0's and 1's. The right side also
denotes any string of 0's and 1's, since 0 and 1 are each in L(0*1*).
22

23. Concretization Test(Conti.)
• NOTE: extensions of the test beyond regular expressions may fail.
• Consider the “law” L  M  N = L  M.
• This is clearly false
– Let L=M={a} and N=Ø. {a}  Ø.
– But if L={a} and M = {b} and N={c} then
– LM does equal L  M  N which is empty.
– The test would say this law is true, but it is not because we are applying
the test beyond regular expressions.
• We’ll see soon various languages that do not have corresponding regular
expressions. 23

24. RE Example for Practice
• Example:
Consider the language, defined over Σ={a , b} of words having at least
one a, may be expressed by a regular expression
(a+b)*
a(a+b)*
.
Consider the language, defined over Σ = {a, b} of words having at least
one a and one b, may be expressed by a regular expression
(a+b)*
a(a+b)*
b(a+b)*
+ (a+b)*
b(a+b)*
a(a+b)*
.
24

25. RE Example for Practice
– Consider the language, defined over Σ={a, b}, of words starting
with double a and ending in double b then its regular expression
may be
aa(a+b)*
bb
– Consider the language, defined over Σ={a, b} of words starting with
a and ending in b OR starting with b and ending in a, then its
regular expression may be
a(a+b)*
b+b(a+b)*
a
25

26. RE Example for Practice
– Consider the language, defined over
Σ={a, b} of words beginning with a, then its regular expression may be
a(a+b)*
– Consider the language, defined over
Σ={a, b} of words beginning and ending in same letter, then its
regular expression may be (a+b)+a(a+b)*
a+b(a+b)*
b
26

27. RE Example for Practice
Consider the language, defined over
Σ={a, b} of words ending in b, then its regular expression may be
(a+b)*
b.
Consider the language, defined over
Σ={a, b} of words not ending in a, then its regular expression may be
(a+b)*
b + Λ. It is to be noted that this language may also be expressed
by ((a+b)*
b)*
.
27

28. RE Example for Practice
ii) (S+
)+
=S+
Solution: since S+
generates all possible strings that can be obtained
by concatenating the strings of S, so (S+
)+
generates all possible
strings that can be obtained by concatenating the strings of S+
,
will not generate any new string.
Hence (S+
)+
=S+
28

29. RE Example for Practice
iii) Is (S*
)+
=(S+
)*
Solution: since Λ belongs to S*
,so Λ will belong to (S*
)+
as
member of S*
.Moreover Λ may not belong to S+
, in general, while
Λ will automatically belong to (S+
)*
.
Hence (S*
)+
=(S+
)*
29

30. RE Assignment
• Exercise: Write a regular expression for the set of strings that
contains an even number of 1’s over ={0,1}. Treat zero 1’s
as an even number.
30

31. Remark
• It may be noted that a language may be expressed by more than one
regular expressions, while given a regular expression there exist a unique
language generated by that regular expression.
31