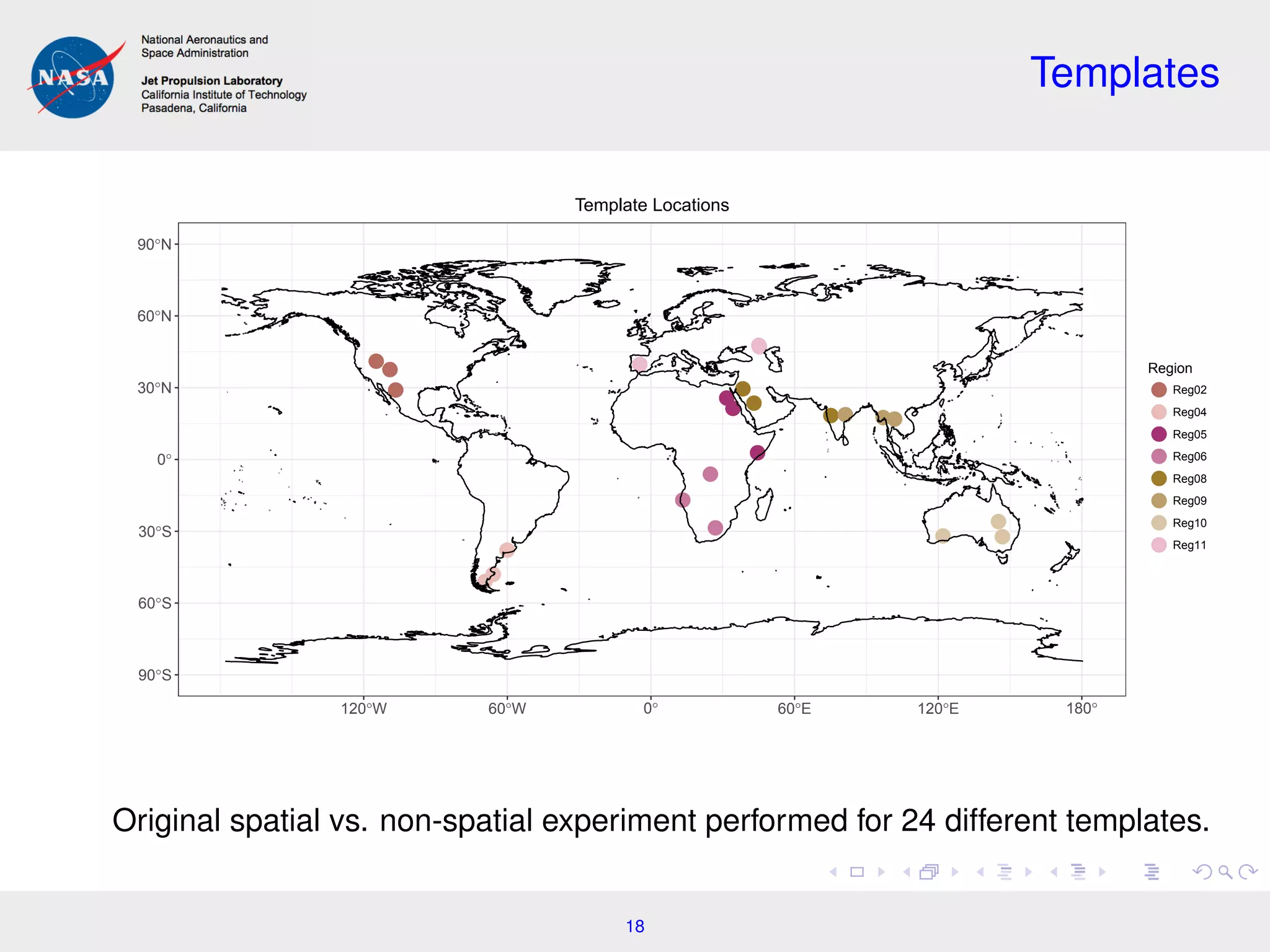
The document discusses incorporating spatial dependence into remote sensing inverse problems, particularly using data from NASA's OCO-2 satellite to improve estimates of atmospheric CO2. It outlines the statistical modeling and hierarchical approaches used to link measurement data to state vectors, highlighting the impact of spatial correlations on retrieval errors. Future work aims to refine these methods for larger spatial domains and enhance the realism of spatial process characterizations.

1. Incorporating Spatial Dependence in Remote
Sensing Inverse Problems
Jon Hobbs1
Joint work with Matthias Katzfuss2
, Veronica Berrocal3
,
Jenný Brynjarsdóttir4
, and Anirban Mondal4
1Jet Propulsion Laboratory, California Institute of Technology
2Texas A&M University
3University of Michigan
4Case Western Reserve University
May 14, 2018
1

2. OCO-2
Satellite data provide a wealth of information for
geoscientists through fine space-time resolution
and extensive coverage.
Satellite-based estimates of carbon dioxide (CO2)
from a collection of satellites, including NASA’s
Orbiting Carbon Observatory-2 (OCO-2), can
provide a more comprehensive constraint on the
carbon cycle.
Remote sensing retrieval provides inference on
atmospheric state given satellite radiances. NASA
produces Level 2 data products with retrieval
results.
Reported uncertainties, or standard errors, dictate
relative weight of CO2 estimates in further
inference.
http://oco.jpl.nasa.gov
2

3. OCO-2 Coverage
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqq
qqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqq
qqqqqqqqqqqqqqqqq
qqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqq
qqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqq
q
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qq
qqqqqqqqqqqqqqqqqqqqqq
qqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqq
q
qqqqqqq
qqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qq
qqqqqqqqqqqqqqqq
qqqq
30
35
40
45
50
−100 −95 −90 −85 −80
46.2
46.5
46.8
−94.0 −93.5
400
405
410
XCO2
Single OCO-2 Orbit, 2016-03-20
3

4. Radiative Transfer
Trace Gas
Absorption
Surface Reflection
Aerosol Scattering
Observed Intensity
Y
Cloud
Scattering
O2
CO2
0.755 0.760 0.765 0.770 0.775
Wavelength
0.000
0.005
0.010
0.015
0.020
Radiance
Surrogate O2
1.59 1.60 1.61 1.62
Wavelength
0.000
0.002
0.004
0.006
0.008
0.010
0.012
Radiance
Surrogate Weak CO2
2.04 2.05 2.06 2.07 2.08
Wavelength
0.000
0.002
0.004
0.006
0.008
0.010
Radiance
Surrogate Strong CO2
Key state variables for
OCO-2 include
CO2 concentration
Pressure
Scattering particles
Surface albedo
4

5. Notation
The atmospheric state is represented as a random vector Xi .
A measurement vector Yi of n elements, representing radiances measured
by the instrument.
The relationship between the state and the expected response is captured
in a forward model, F(Xi , B).
A vector of forward model parameters, B, captures other quantitative
characteristics of the forward model.
A statistical model links the measurement vector, Yi , to the state vector, Xi ,
Yi = F(Xi , B) + i .
5

6. Statistical Model
Consider a hierarchical model for a single pixel/footprint,
Xi ∼ MVN (µi , Σi )
Yi |Xi , B ∼ MVN (F(Xi , B), Σ )
Σ = Var ( i )
The conditional distribution can be used for inference on the state,
−2 ln[Xi |Yi , B] = (Yi − F(Xi , B))T
Σ−1
(Yi − F(Xi , B))
+ (Xi − µi )T
Σ−1
i (Xi − µi ) + constant.
6

7. State Vector
The state vector for footprint i can be partitioned into the CO2 and non-CO2
components
Xi = Xi,a Xi,b Xi,c Xi,d
T
Xi,a =


Xi,1 : CO2 concentration at level 1
. . .
Xi,20 : CO2 concentration at level 20


Xi,b = Xi,21 : Surface pressure
Xi,c =


Xi,22 : Albedo coefficient 1
. . .
Xi,27 : Albedo coefficient 6


Xi,d =


Xi,28 : Aerosol type 1, coefficient 1
. . .
Xi,39 : Aerosol type 4, coefficient 3


Above state vector configuration for the OCO-2 surrogate model (Hobbs et
al., 2017)
7

8. Single Footprint
Primary quantity of interest, XCO2 is a pressure weighted average of the
CO2 profile,
XCO2 = hT
Xi,a
The distribution for an individual footprint is taken to be Gaussian,
Xi ∼ MVN(µi , Σi )
Σi =




Σi,aa 0 0 0
0 Σi,bb 0 0
0 0 Σi,cc 0
0 0 0 Σi,dd




8

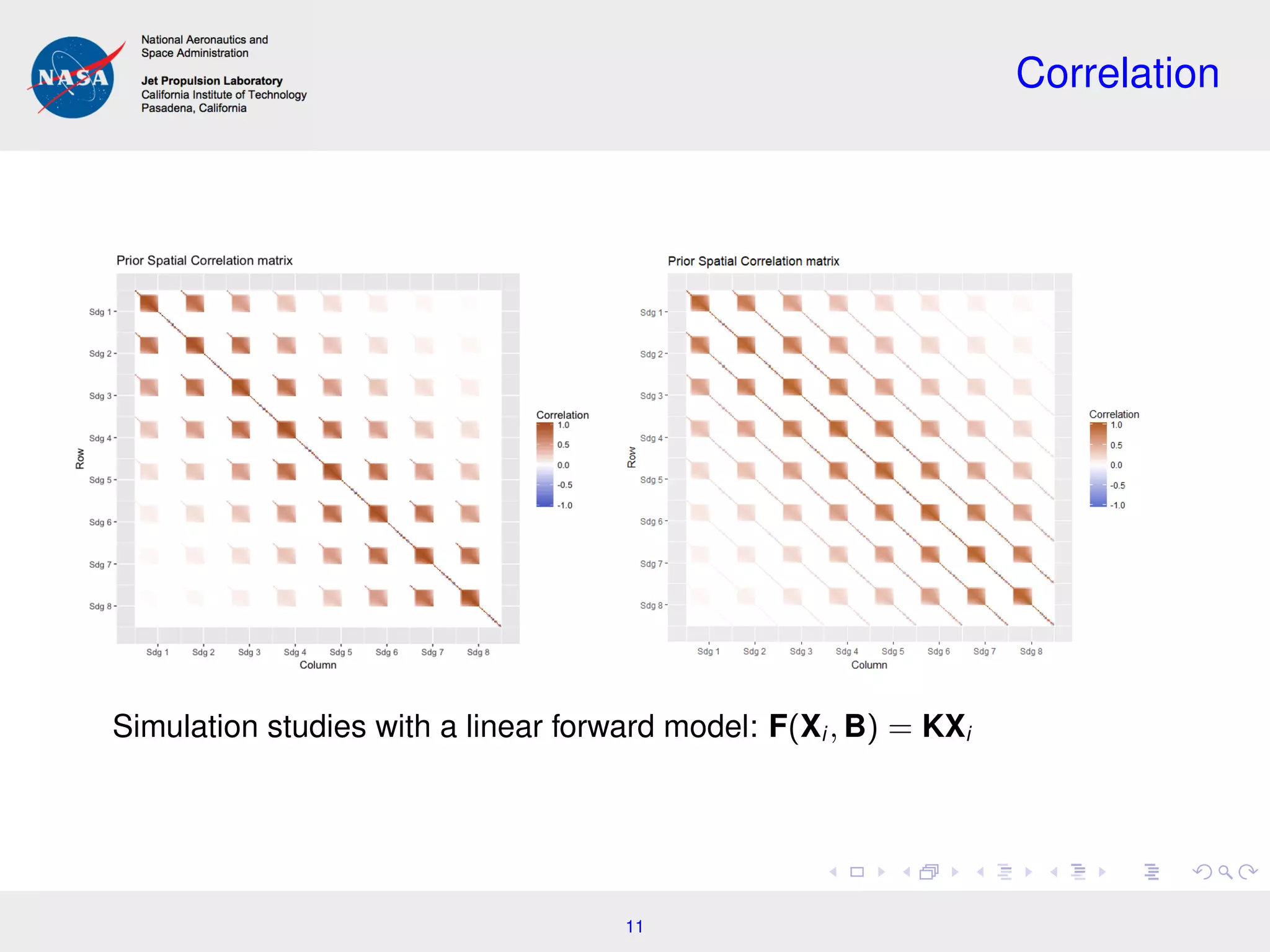
9. Spatial Case
Consider, X = [X1 X2 . . . X8] , a collection of state vectors along an
eight-footprint transect:
X1 X2 X3 X4 X5 X6 X7 X8
Joint distribution
X ∼ MVN(µ, Σ)
Cost function
−2 ln[X|Y, B] =
8
i=1
(Yi − F(Xi , B))T
Σ−1
(Yi − F(Xi , B))
+ (X − µ)T
Σ−1
(X − µ) + constant.
Example of a multi-pixel retrieval (Dubovik et al., 2011)
9

10. Parameters
Modeling considerations: What choices impact retrieval error distribution?
Nature of cross-footprint spatial dependence
Dubovik et al. (2011) use Gaussian Markov random field.
Atmospheric CO2 spatial dependence is smooth; we consider Matern.
Site-specific atmospheric and instrument specifications motivate
geophysical templates.
Additive error in likelihood
Error covariance Σ typically assumed diagonal.
Correlations across wavelengths and/or space can be considered.
10

11. Correlation
Simulation studies with a linear forward model: F(Xi , B) = KXi
11

12. Discrepancy
For the OCO-2 linear model investigation, an alternative representation is
proposed:
X ∼ N(µX, ΣX)
Y = KX + δ +
∼ N(0, Σ )
δ = HZ
The “model discrepancy” component δ introduces correlation into the
radiances, with H being a small collection of eigenvectors, and Z being a
random vector with a diagonal covariance of eigenvalues,
Z ∼ N(0, ΣZ)
12

13. Four retrievals
An operational algorithm assumes fixed values for other parameters,
Retrieval prior mean µa → µ
Retrieval prior covariance Σa → Σ
Retrieval error variance Σe → Var(Y|X)
Four different retrievals considered
Name Assumed Prior: Σa Assumed Var(Y|X): Σe
NonSpat_Corr Independent Var(δ + )
NonSpat_Diag Independent Σ
Spatial_Corr Spatial Var(δ + )
Spatial_Diag Spatial Σ
Methods compared using standard deviation of XCO2 retrieval error
No bias in this configuration
Possible additional metric: compare to each methods reported standard
error
13

14. Retrieval Error
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
0.5
0.6
0.7
0.8
FP1 FP2 FP3 FP4 FP5 FP6 FP7 FP8
Footprint
ErrorStdDev[ppm]
Model
q
q
q
q
NonSpat_Corr
NonSpat_Diag
Spatial_Corr
Spatial_Diag
Retrieval Error Variability
14

15. Operational Prior
The true variability embedded in Σ attempts to reflect real variability over a
region within a short time period (weeks).
Corresponding XCO2 standard deviations are 2-5 ppm.
The OCO-2 operational prior is far looser; the prior standard deviation is 14
ppm.
Modified experiment uses Σ as true variability but uses OCO-2 operational
prior covariance Σa in retrieval.
15

16. Retrieval Error
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
0.8
1.0
1.2
1.4
FP1 FP2 FP3 FP4 FP5 FP6 FP7 FP8
Footprint
ErrorStdDev[ppm]
Model
q
q
q
q
NonSpat_Corr
NonSpat_Diag
Spatial_Corr
Spatial_Diag
Retrieval Error Variability
Operational Prior
16

17. Templates
Simulations Under Varying Template Conditions
17

18. Templates
qq
q
q
qq
q
q
q
q
q
q
q
q
q qq q
qq
q
qq
q
90°S
60°S
30°S
0°
30°N
60°N
90°N
120°W 60°W 0° 60°E 120°E 180°
Region
q
q
q
q
q
q
q
q
Reg02
Reg04
Reg05
Reg06
Reg08
Reg09
Reg10
Reg11
Template Locations
Original spatial vs. non-spatial experiment performed for 24 different templates.
18

19. Templates
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
0.0
0.5
1.0
02 04 05 06 08 09 10 11
Region
ErrorStdDev[ppm]
Model
q NonSpatial
Spatial
Region Errors
Retrieval error standard deviation for Footprint 4.
19

20. Discussion
Future Work
Characterize bias of spatial retrieval when prior mean misspecified
Extend to larger spatial domain
Nonlinear case with iterative optimization using OCO-2 operational forward
model
Individual likelihood evaluations can be parallelized
Spatial prior density is relatively cheap to evaluate
Characterize spatial process for state vector components using available
data for additional realism
Joint inference for spatial dependence parameters in Σ, (Wang et al., 2013)
Manuscript plans
End of 2018: Review and lessons learned for linear case
2019: Opeartional setting for OCO-2 over extended domain
20

21. Acknowledgments
Suggestions and contributions from Amy Braverman, Annmarie Eldering,
Mike Gunson, Susan Kulawik, Mikael Kuusela, Jessica Matthews, Vijay
Natraj, and Zhengyuan Zhu are appreciated.
Questions?
Jonathan.M.Hobbs@jpl.nasa.gov
c 2018 California Institute of Technology. Government sponsorship
acknowledged.
21

22. References
References
Dubovik, O. et al. (2011). Statistically optimized inversion algorithm for enhanced retrieval of aerosol
properties from spectral multi-angle polarimetric satellite observations. Atmos. Meas. Tech.,
4:975–1018. doi:10.5194/amt-4-975-2011.
Hobbs, J., Braverman, A., Cressie, N., Granat, R., and Gunson, M. (2017). Uncertainty quantification
for retrieving atmospheric CO2 from satellite data. SIAM/ASA J. Uncertainty Quantification,
5:956–985.
Rodgers, C. D. (2000). Inverse Methods for Atmospheric Sounding. World Scientific, Hackensack, NJ.
Wang, Y., Jiang, X., Yu, B., and Jiang, M. (2013). A hierarchical Bayesian approach for aerosol retrieval
using MISR data. J. Amer. Stat. Assoc., 108:483–493. doi:10.1080/01621459.2013.796834.
22

23. Supplement
Linear Error Calculation
23

24. Supplement
Additional useful quantities include
Random error variance Σe,
Gain,
G = K Σ−1
e K + Σ−1
a
−1
K Σ−1
e
Averaging kernel,
A = GK
Linear retrieval error can be decomposed as
∆ = ˆX − X
= (A − I) (X − µa) smoothing
+ G (δ + ) noise
(Rodgers, 2000; Hobbs et al., 2017)
24