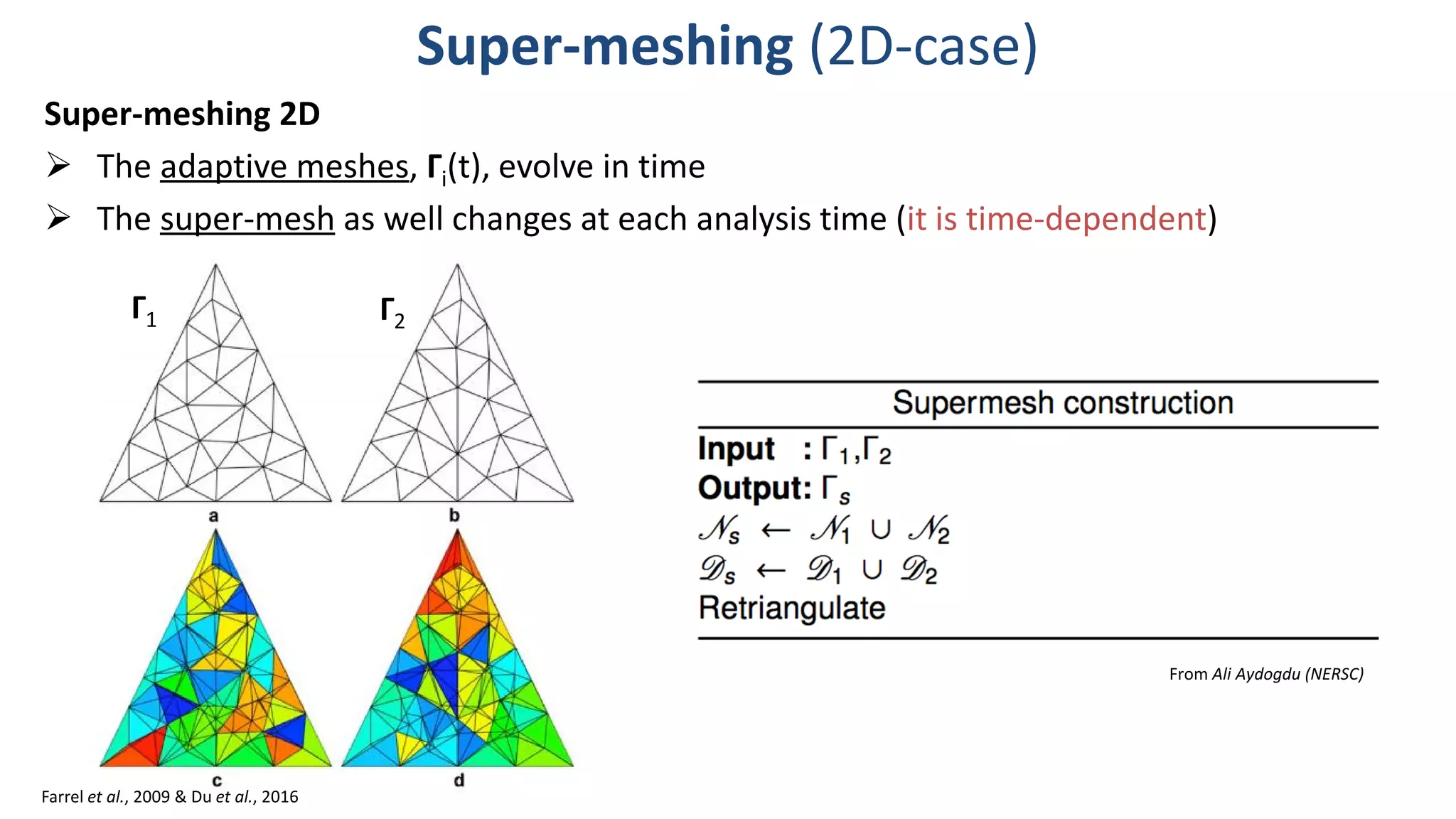
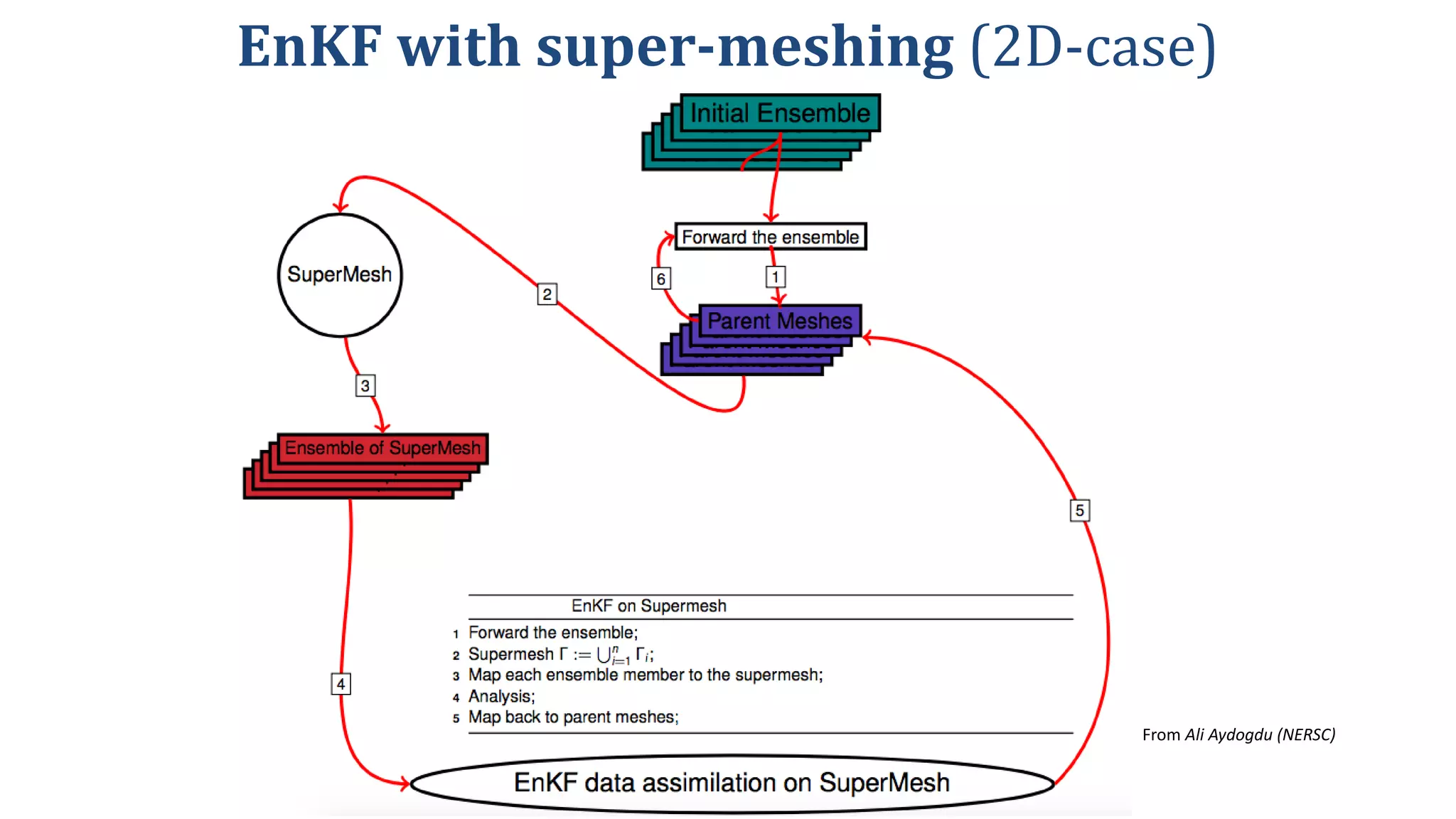
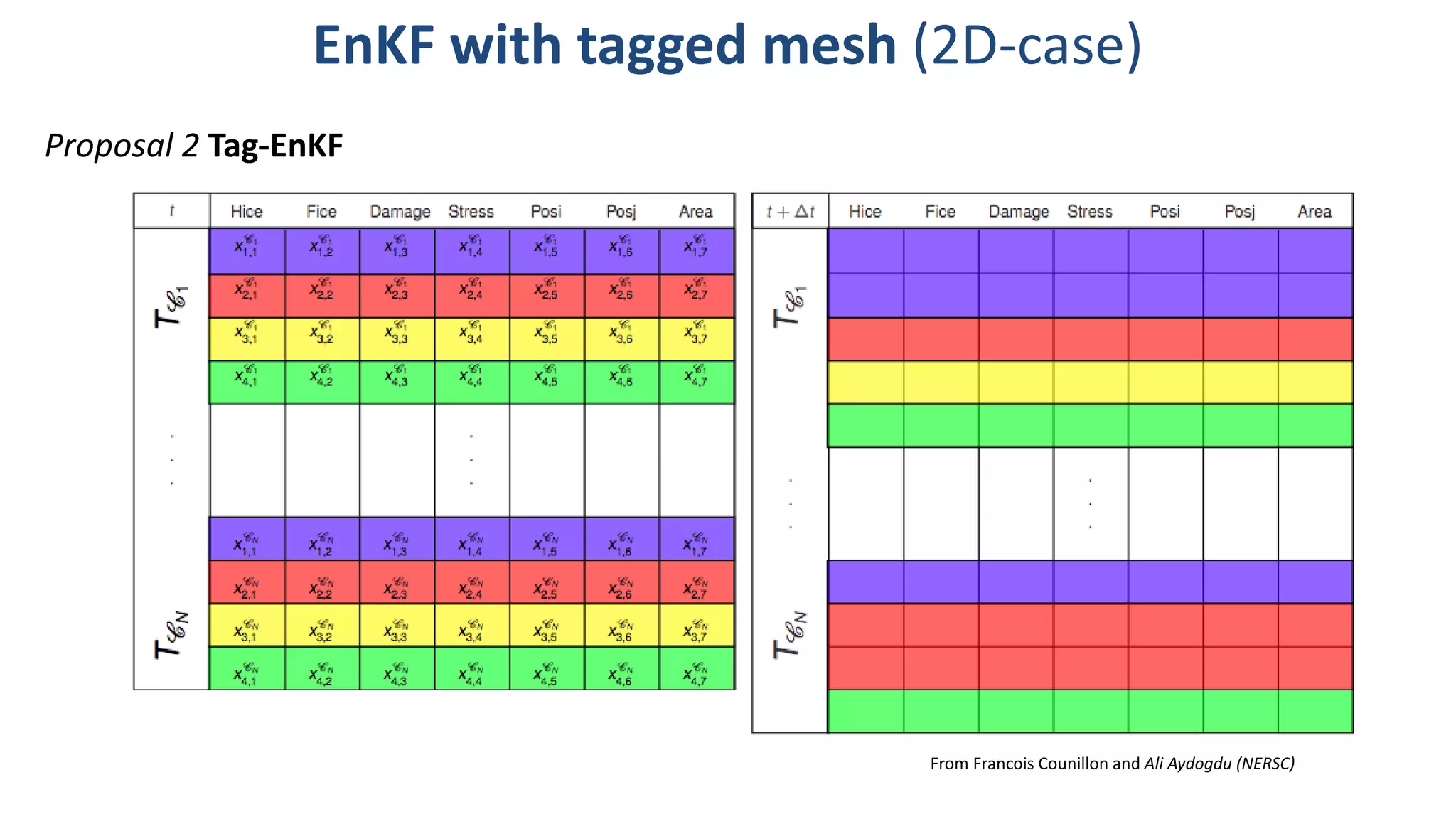
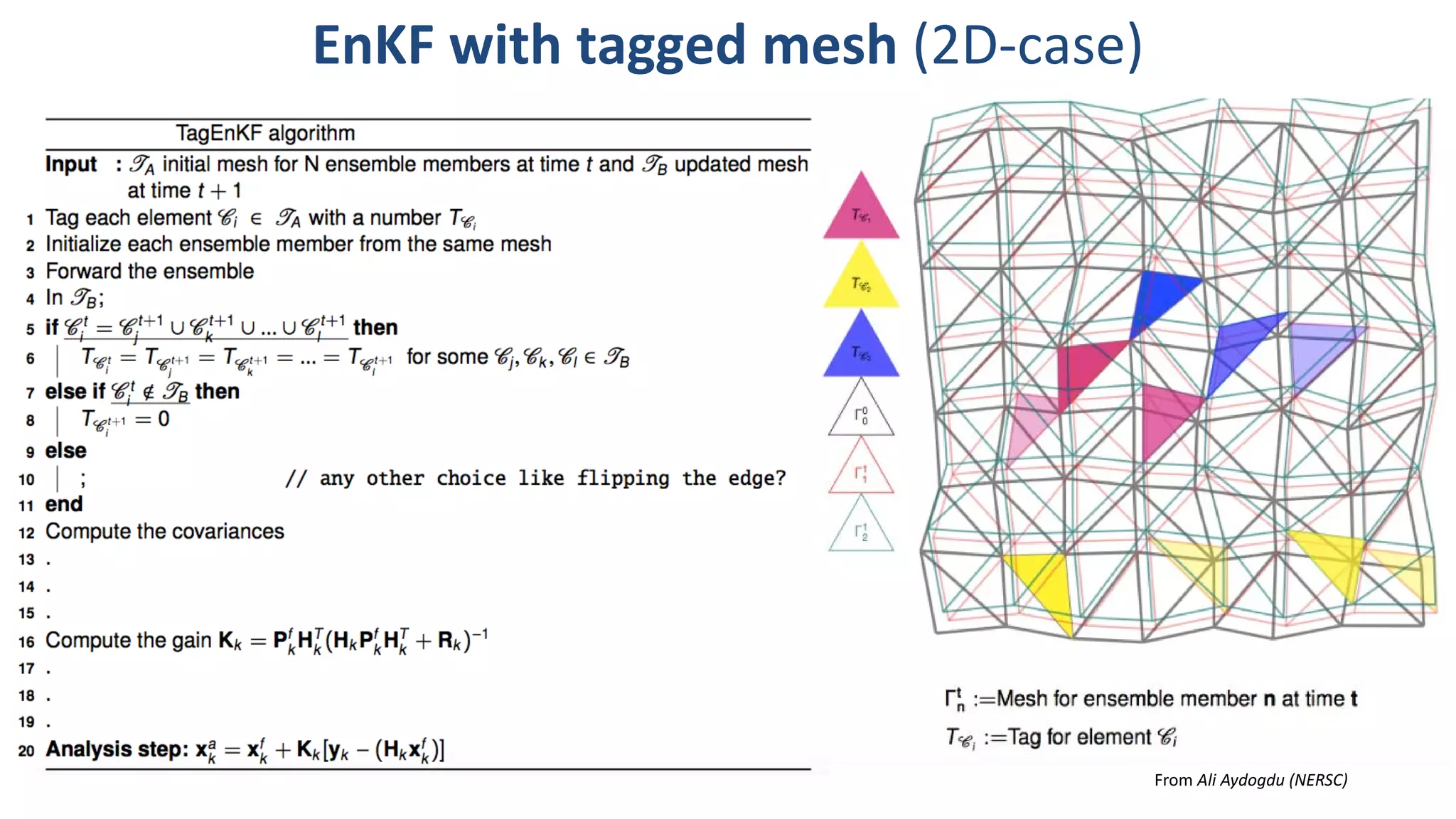
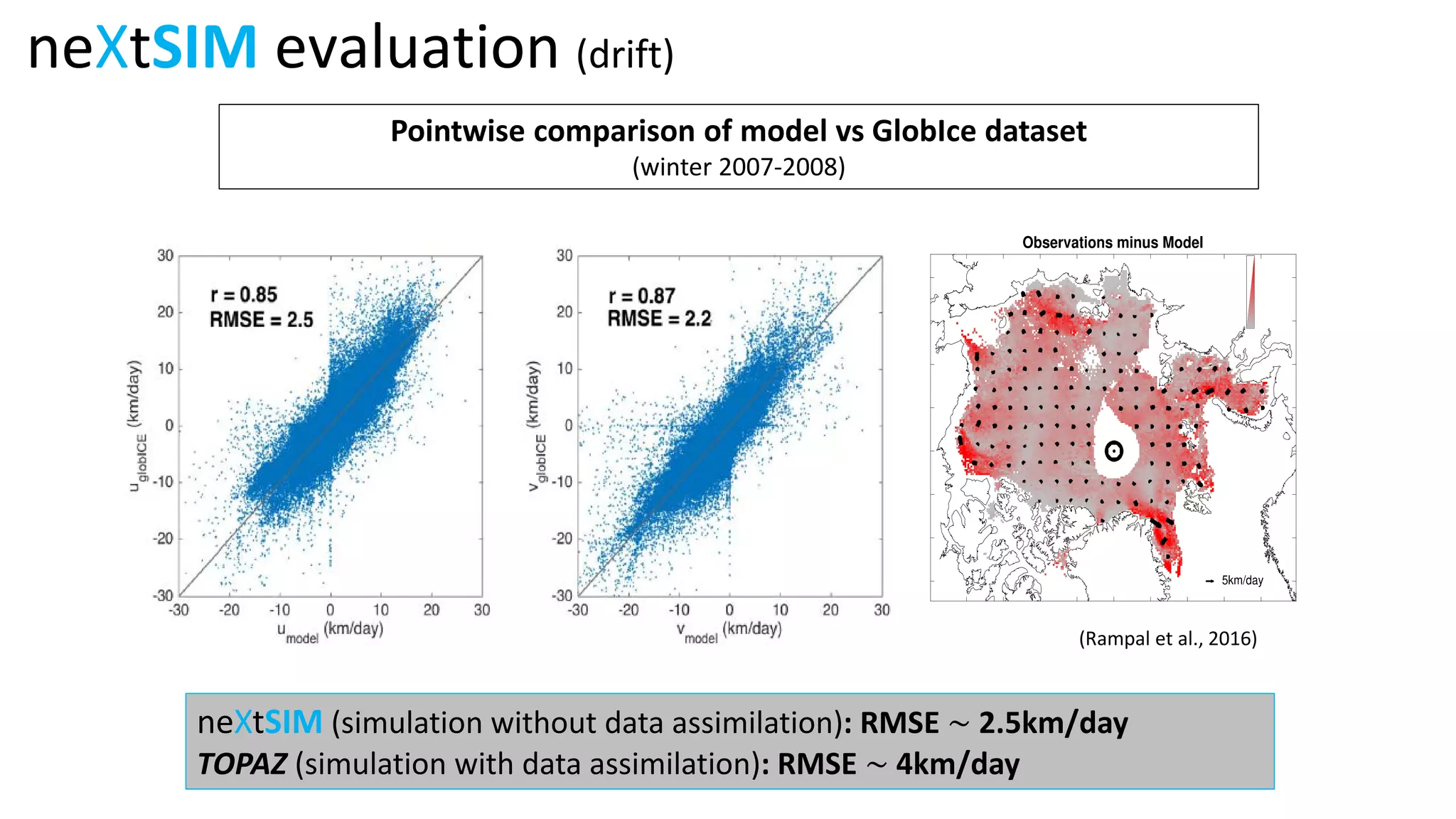
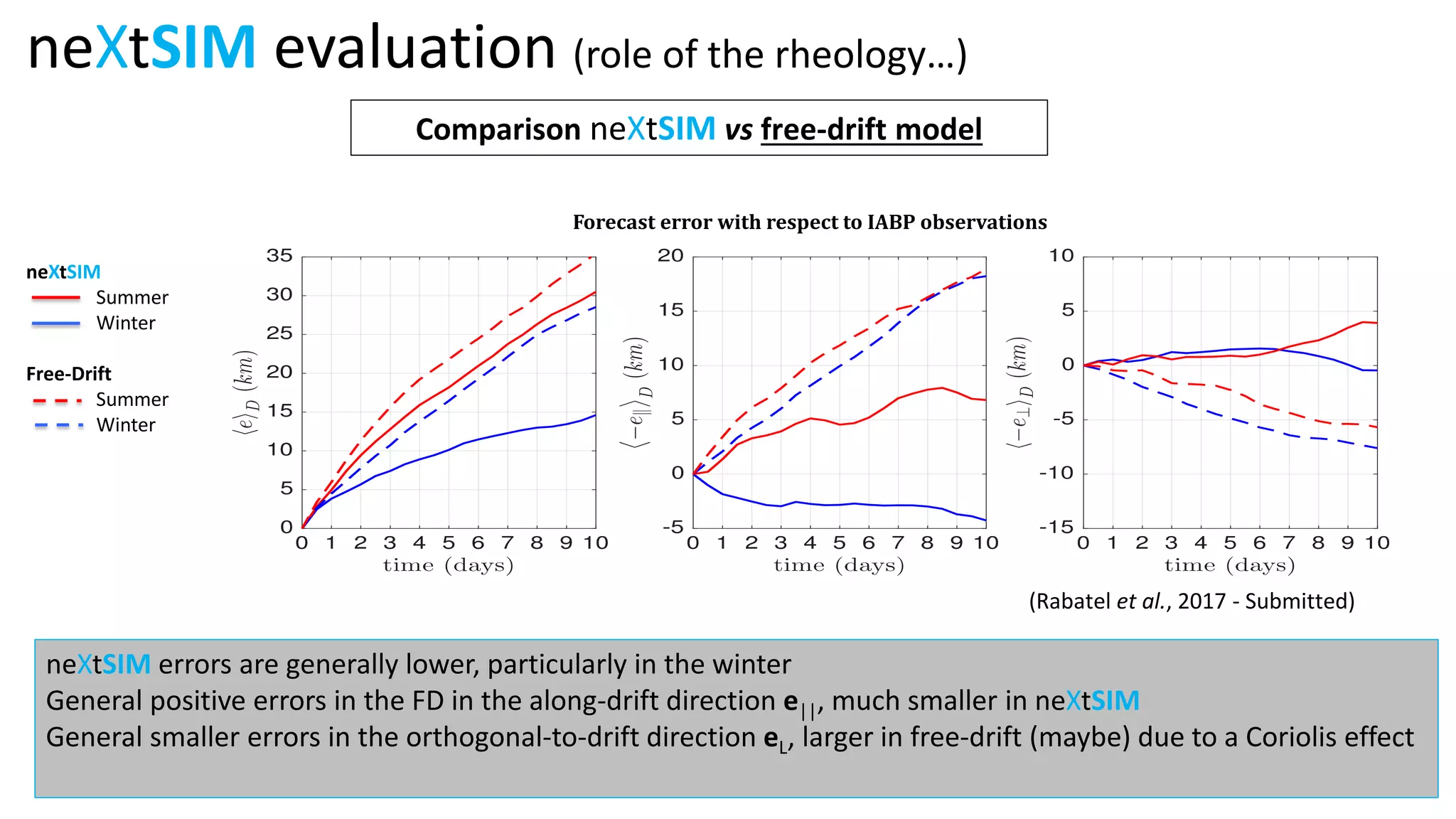
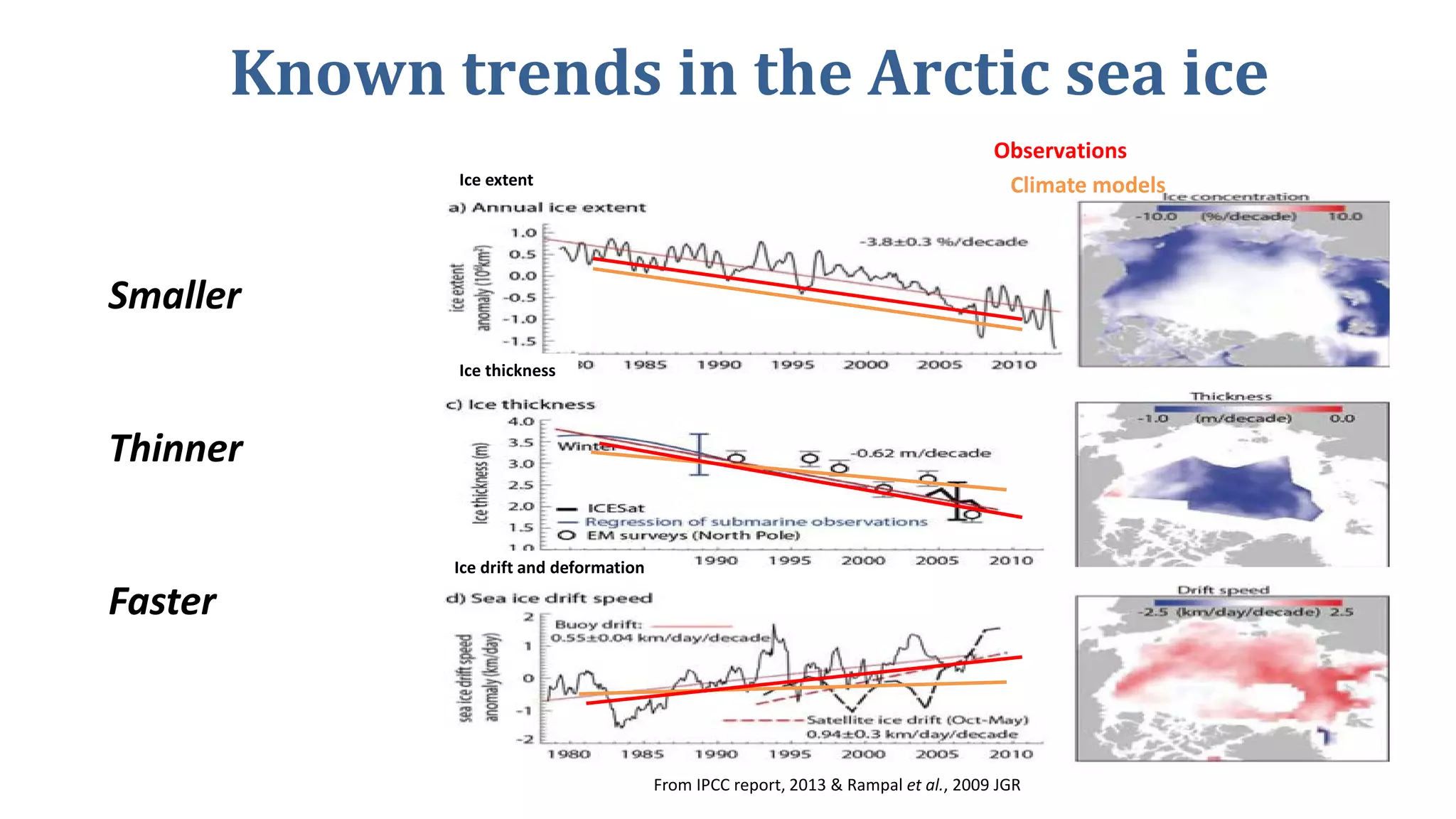
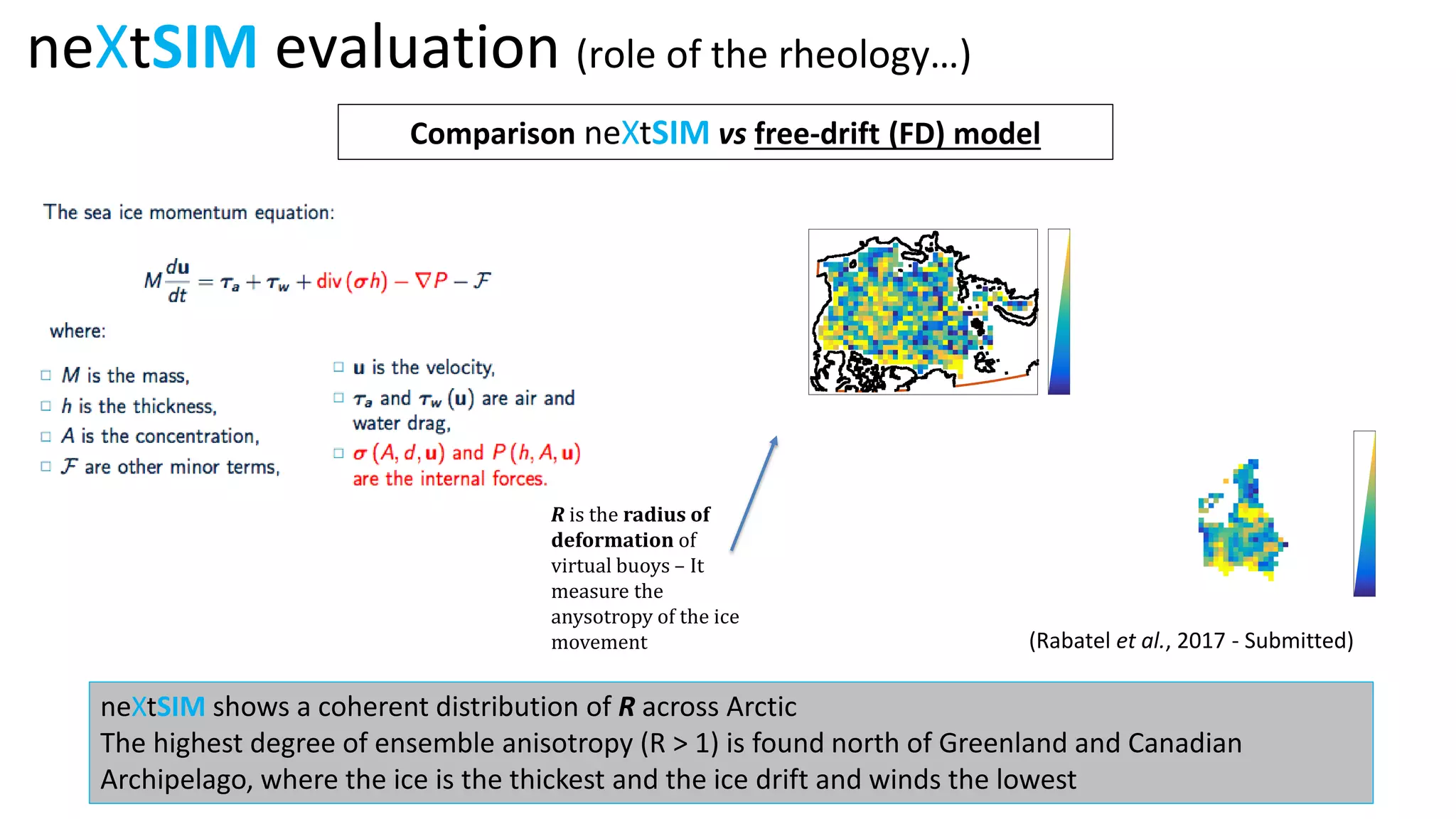
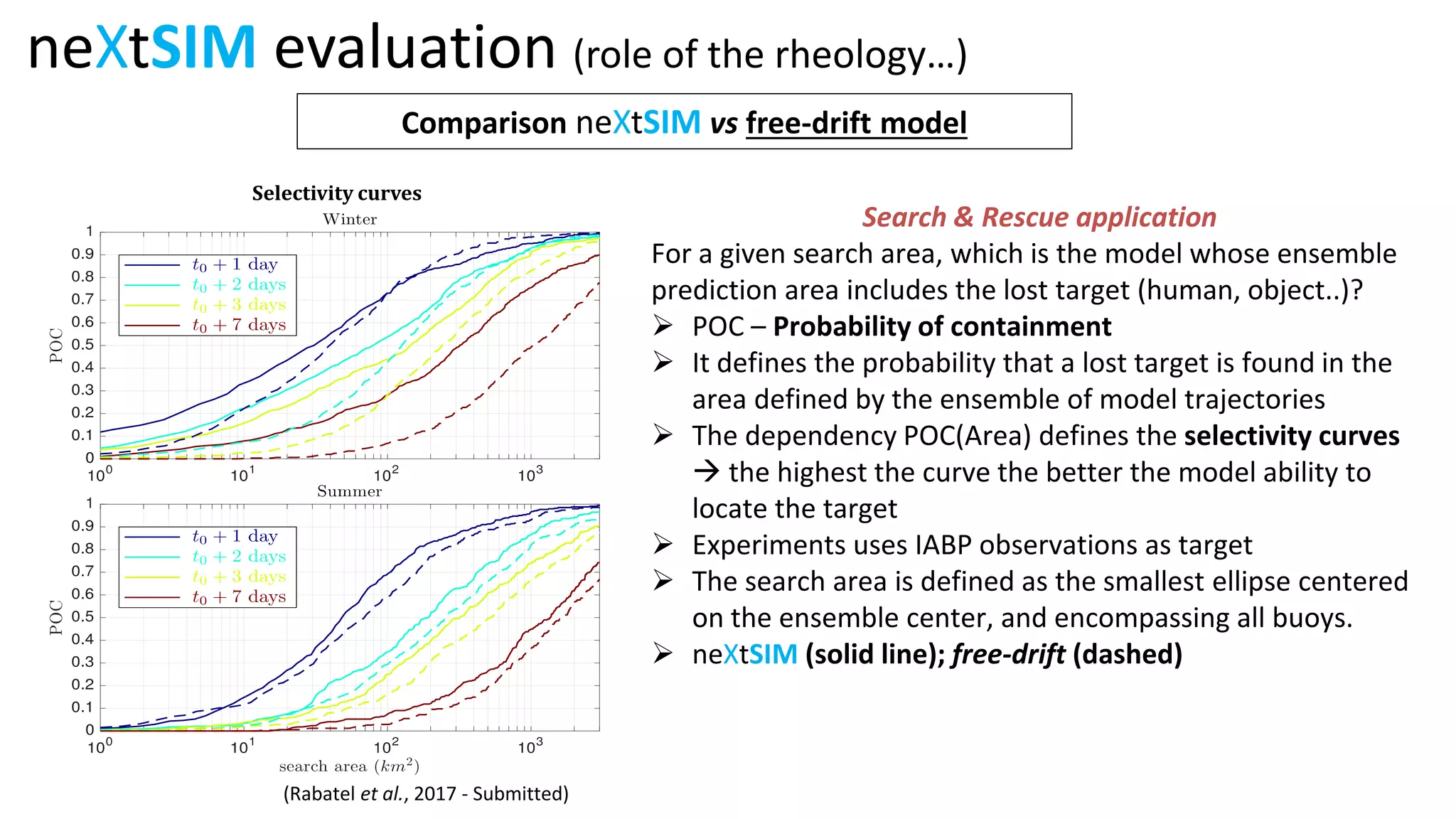
The document presents a new Lagrangian model for sea ice that addresses the shortcomings of existing methods, particularly in data assimilation and ice mechanics. It discusses the operational and simulation performance of the model, including comparisons with previous systems, and highlights issues like biases, variability, and the need for better data assimilation techniques. The findings emphasize the model's capability to simulate sea ice dynamics accurately, while proposing new methodologies for integrated data approaches.

1. A new Lagrangian model of the sea ice and
related issues for data assimilation
Alberto Carrassi
C. Guider and C.K.R.T. Jones
M. Rabatel, P. Rampal,
L. Bertino and Ali Aydogdu

2. Outline
1. Why a different treatment of the sea-ice mechanics?
2. A novel solid/elastic Lagrangian sea-ice model
3. Issues related to the design of data assimilation methods

3. Known trends in the Arctic sea ice
From IPCC report, 2013 & Rampal et al., 2009 JGR
Ice extent
Ice thickness
Ice drift and deformation
Climate models
Observations
Smaller
Thinner
Faster

4. The TOPAZ monitoring system
 Operational at MET Norway
o Since 2008 ocean coupled to the sea-ice
o Ecosystem coupled online in Jan. 2012
 25 years reanalysis at NERSC
o EnKF (100 members)
o ~ 4 million CPU hours
 Copernicus (Arctic MFC)
o 10-mems ensemble forecast
o Free distribution
o Dynamical viewing
Ice area forecast for Today
(start date 13th August – 9 days before)

5. Ice drift in real time
TOPAZ OSI-SAF
Example 3-days 6th-8th December 2015
Patterns are OK, but the spatial variability of ice drift are too smooth
Even though OSI SAF Data is assimilated

6. In other systems (ORA IP)
Same problem as in TOPAZ (smooth gradients), large model diversity
Chevallier et al. Clim. Dyn. 2016.

7. TOPAZ Reanalysis
 Input:
o SAR based ice drift data
 Bias 1-2km/day
o Can be fine tuned with model
parameters (wind drag)
 Even in reanalysis mode, RMS errors
of about 4km/day
o High compared to the signal (5 to
10 km per day)
o Wind forcing is not the only
problem
o Ice parameters?
o Ice rheology?
http://cmems.met.no/ARC-
MFC/V2Validation/timeSeriesResults/index.html (Xie et al., 2017)

8. Ice drift seasonality in TOPAZ
shortcoming of the EVP rheology?
The seasonal cycle is off phase
Aligned with the wind intensity but not sensitive to the cycle of ice thickness.
Tuning drag parameters does not help.
IABP
Free run
TOPAZ
Re-tuned
Xie et al. 2017

9. Ice drift seasonality in other systems
shortcoming of the EVP rheology?
(Rampal et al. 2011)
Normalized annual cycle of sea-ice drift
• Models are shown with continuous lines
• Observations (IABP) in dashed red line
• Cycles have been averaged over 10 years
(1997-2007)
The seasonal cycle is off phase
……

10. Status from present/day forecasts
EVP rheology (as used in TOPAZ)
• Biases
– No acceleration of ice
– Seasonality phased off
– Tuning with model
parameters is problematic
(although for some
models it works)
• Lack of variability
– Spatially and temporally
too smooth
– High RMS errors of drift
trajectories
Time to examine a completely different ice model

11. Modelling challenges – Sea ice dynamics
shear rate
(/day)
NASA, Modis
NASA, Radarsat1
How to simulate sea ice fracturing/deformation and the associated scaling invariance properties
with a continuous model ?
Spatial heterogeneity (… of fractures/faults patterns)
Temporal intermittency (… of ice quakes/earthquakes)
Does a universal brittle behavior of
“2D” geophysical solids exist?
Analogy: sea ice cover - Earth crustLarge-scale deformation Local fracturing
Marsan et al., PRL, 2004 ; Rampal et al., JGR, 2008 ; Weiss et al., EPSL 2009
Point Barrow
∼ 2000 km

12. Sea ice mechanic  Maxwell Elasto-Brittle rheology
 NEW variable: the level of damage “d” associated to each grid cell
 simulates the ice failure
 allow for extremely localized deformation (divergence/ridging)
New Physics
neXtSIM, in a nutshell …
Damage
neXtSIM
Initial zero damage
3 days of simulation
Period: December 2015
Forcing with realistic wind and current
Resolution ≈1 Km
Initial thickness and concentration from satellite data
Area: Fraim strait
Complex pattern of damage after 3
days.
Ice in pieces of different sizes
Behavior caused only by the
external forcing

13. Numerics
 Finite element method
u, vP1
Unstructured grid  Adaptive mesh
and local remeshing
u,
v
 Fully Lagrangian / ALE
t
t+∆t
neXtSIM, in a nutshell …

14. neXtSIM, in a nutshell …
Lagrangian advection sheme / Dynamical-local remeshing

15. neXtSIM evaluation (volume, extent and area)
neXtSIM is reproducing the annual cycles of sea ice volume, extent and area
Comparison between model and CryoSAT2+SMOS, and SSMI/S datasets
(Nov 2010- Aug 2012)
volume extent area
CS2+SMOS Passive Micro. Passive Micro.

16.  neXtSIM run
o Free run
o Drag optimized to free drifting ice
 Comparison to SAR-based ice drift
o RGPS and GlobIce
o Oct 2007 to April 2008
 Average and median errors much lower
than TOPAZ (4 km/day)
(Rampal et al. 2016)
neXtSIM (simulation without data assimilation): RMSE ∼ 2.5km/day
TOPAZ (simulation with data assimilation): RMSE ∼ 4km/day
neXtSIM evaluation (drift)

17. neXtSIM shows a coherent distribution of R across Arctic
The highest degree of ensemble anisotropy (R > 1) is found north of Greenland and Canadian
Archipelago, where the ice is the thickest and the ice drift and winds the lowest
neXtSIM evaluation (role of the rheology…)
Comparison neXtSIM vs free-drift (FD) model
(Rabatel et al., 2017 - Submitted)
R is the radius of
deformation of
virtual buoys – It
measure the
anysotropy of the ice
movement

18. neXtSIM evaluation (role of the rheology…)
Comparison neXtSIM vs free-drift model
Search & Rescue application
For a given search area, which is the model whose ensemble
prediction area includes the lost target (human, object..)?
POC – Probability of containment
It defines the probability that a lost target is found in the
area defined by the ensemble of model trajectories
The dependency POC(Area) defines the selectivity curves
 the highest the curve the better the model ability to
locate the target
Experiments uses IABP observations as target
The search area is defined as the smallest ellipse centered
on the ensemble center, and encompassing all buoys.
ne XtSIM (solid line); free-drift (dashed)
Selectivity curves
(Rabatel et al., 2017 - Submitted)

19. Data assimilation with neXtSIM
Issues
 Mesh varies in time
 Remeshing procedure that does not
conserve the total number of elements
 Large computational model with physical
variables at both vertices and centers
 Variety of data types (satellite and in-situ)
In (standard) DA
the state vector reads
where n=mk with
• k = number of physical quantities
• m = number of grid points
In particular in neXtSIM
 Grid points include vertices (v) and centers (c), so that n=mvkv+mckc
 Both mv and mc may change in time
 Vertices and Centers must be treated differently as different physical variables are
associated with each
 Particularly problematic for ensemble-based DA methods (EnKF-like)

20. Data assimilation with neXtSIM
Two “proposals”
Proposal 1
Super-meshing
Reference each grid points with a
“common” fixed supermesh
At most one vertex in each mesh box
At analysis time ”project” the individual
mesh on the supermesh
Perform the analysis on the supermesh
The supermesh can be fixed in time or
change at each analysis times

21. Super-meshing
1D-case
Proposal 1
Super-meshing 1D
The super-mesh is fixed (time
independent)
The adaptive mesh, z(t), evolves in time
It is valid if
 δ1 = minimum grid point distance
 δ2 = maximum grid point distance
Otherwise it is re-meshed
Guider et al., 2017 - In preparation

22. Super-meshing (1D-case)
Re-meshing 1D
(Guider et al., 2017 - In preparation)

23. Super-meshing (1D-case)
Defining the state space
Mesh point Physical variable

24.  The ensemble members will generally have different meshes, so they may have different
active cells.
 For 1≤i≤N and 1≤i1,i2≤N define the sets
EnKF with super-meshing (1D-case)
 State-augmentation formulation
 Compute the mean and covariance as
 Ji and Ji1,i2 may have different size --> Mean and covariance can be based on different
sample (statistical consistency issue!)
Guider et al., 2017 - In preparation

25.  The analysis, at time tk, is performed with the stochastic EnKF
EnKF with super-meshing (1D-case)
 Define the observation operator
with the Kalman gain

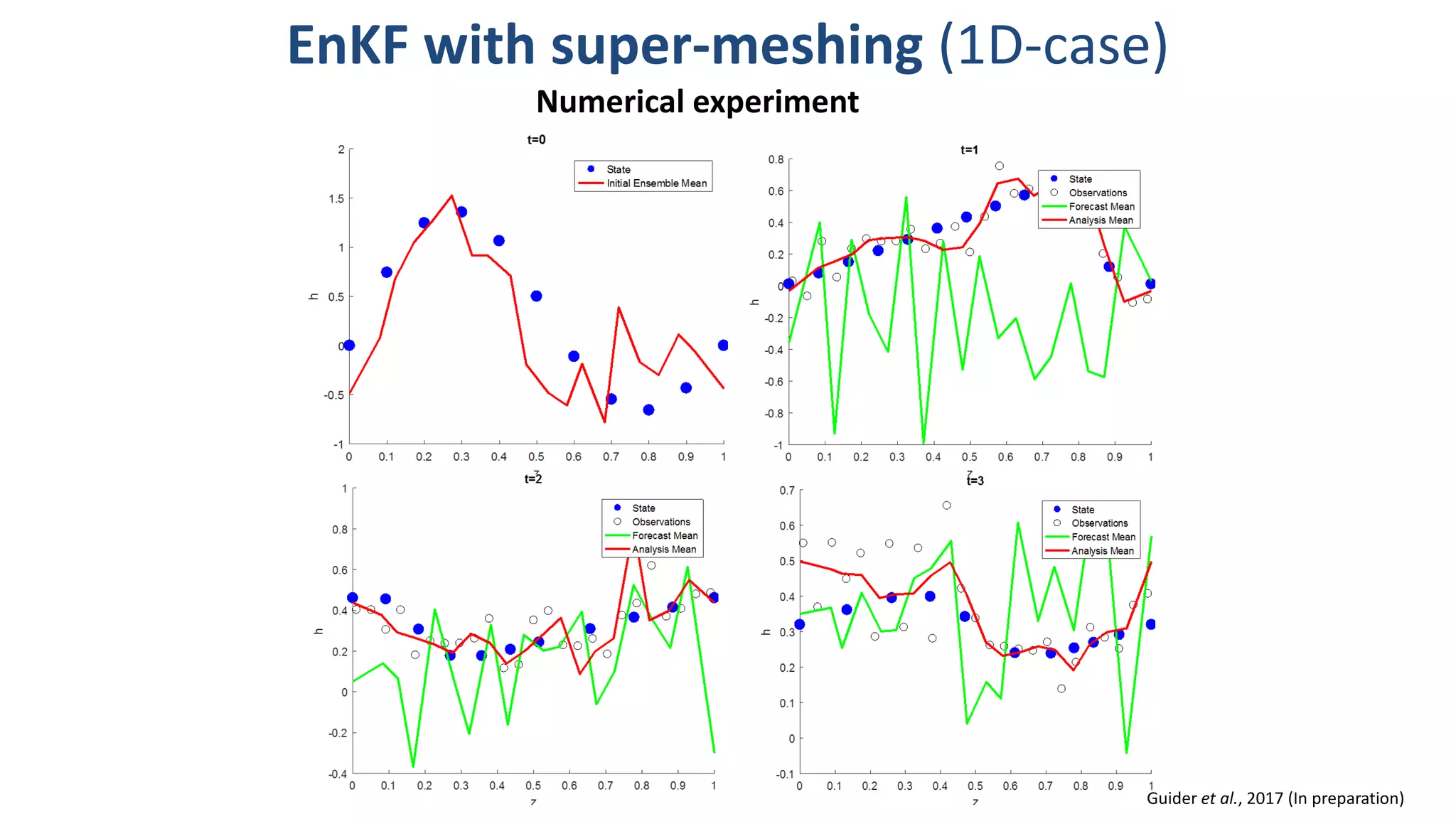
26. EnKF with super-meshing (1D-case)
Guider et al., 2017 (In preparation)
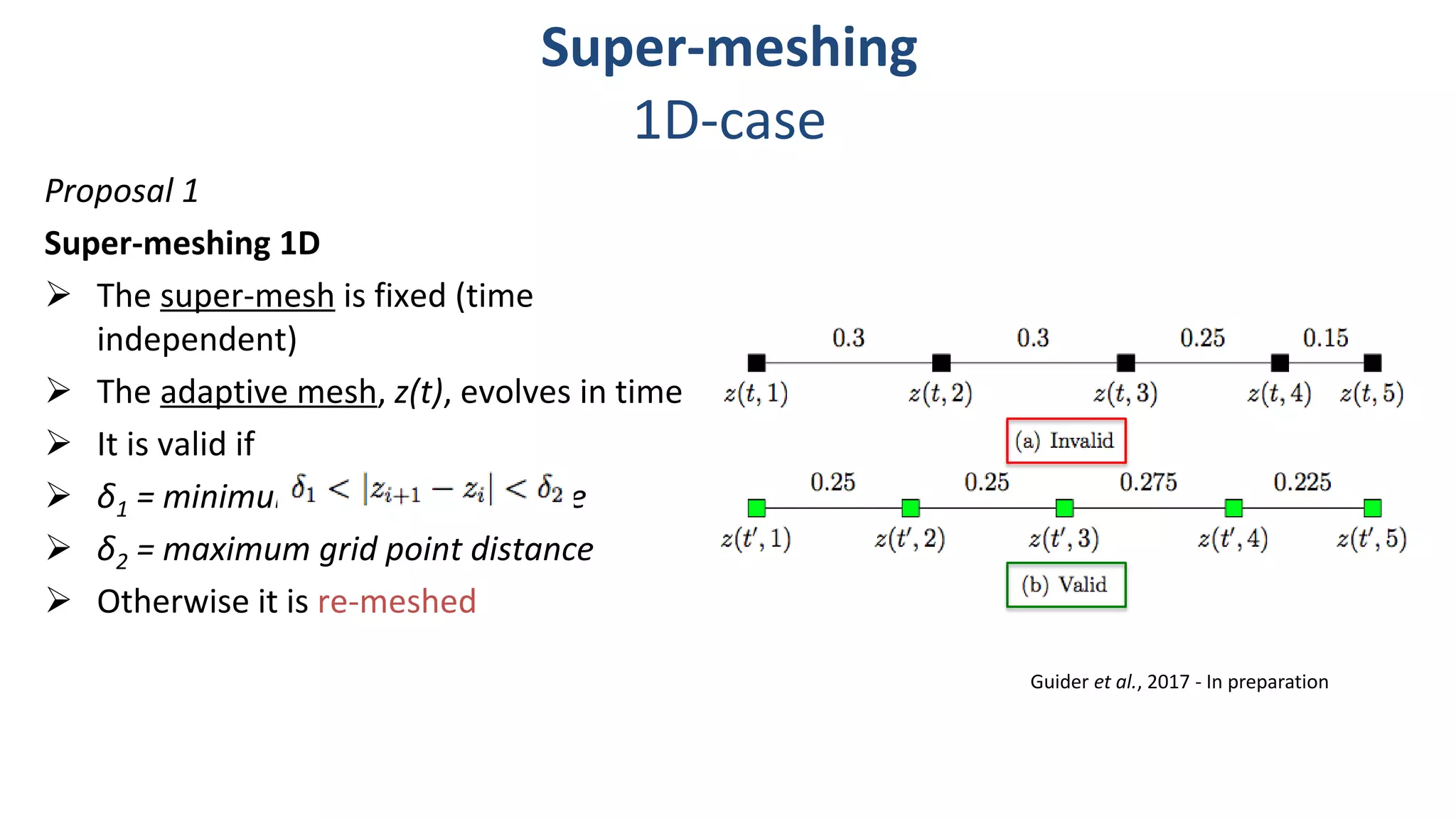
Numerical experiment
 The adaptive mesh, z(t), evolves as
The physical variable, h(t), evolves
following the Burgers’ equation
 The fixed super-mesh has N=50 cells and δ1/δ2 =
0.05/0.15
 EnKF with Ne=50 members
 25 observations evenly spaced over [0,1]

27. EnKF with super-meshing (1D-case)
Numerical experiment
Guider et al., 2017 (In preparation)

28. Super-meshing (2D-case)
Super-meshing 2D
 The adaptive meshes, Γi(t), evolve in time
 The super-mesh as well changes at each analysis time (it is time-dependent)
Γ1 Γ2
Farrel et al., 2009 & Du et al., 2016
From Ali Aydogdu (NERSC)

29. EnKF with super-meshing (2D-case)
From Ali Aydogdu (NERSC)

30. EnKF with tagged mesh (2D-case)
From Francois Counillon and Ali Aydogdu (NERSC)
Proposal 2 Tag-EnKF

31. EnKF with tagged mesh (2D-case)
From Ali Aydogdu (NERSC)

32. Conclusion …
• Spatio-temporal varying mesh sets an issue for developing compatible
DA methods
• Ideally one may include the uncertainty in the mesh itself –>
Problematic given the usual huge size
• In-situ observations are Lagrangian by construction –> Their assimilation
in Lagragian model may thus be facilitated
• Satellite measurements of ice drift are expected to have the larger
impact
• Complexity of observation operator using EM radiation to infer physical
variables is a central issue.

33. Essential bibliography
Bouillon, S. and P. Rampal: Presentation of the dynamical core of neXtSIM, a new sea ice model, Ocean Modelling, 91, 23–37, 2015.
Bouillon, S. and P. Rampal: On producing sea ice deformation data sets from SAR-derived sea ice motion, The Cryosphere, 9, 663–673,
2015.
Guider, C., M. Rabatel, A. Carrassi and C.K.R.T. Jones: Data assimilation on a non-conservative adaptive mesh. Geophysical Research
Abstracts, vol. 19, EGU2017-706
Rabatel, M., P. Rampal, A. Carrassi, L. Bertino and C.K.R.T. Jones: Probabilistic forecast using a Lagrangian sea ice model - Application
for search and rescue operation. The Cryosphere, 2017 (submitted)
Rabatel, M., P. Rampal, A. Carrassi, L. Bertino and C.K.R.T. Jones: Sensitivity analysis of a Lagrangian sea ice model. Geophysical
Research Abstracts, vol. 19, EGU2017-688
Rampal , P., Weiss, J., Marsan, D., and Bourgoin, M.: Arctic sea ice velocity field: general circulation and turbulent-like fluctuations, J.
Geophys. Res., 114, 2009.
Rampal , P., Weiss, J., Dubois, C., and Campin, J. M.: IPCC climate models de not capture Arctic sea ice drift acceleration: Consequences
in terms of projected sea ice thinning and decline, J. Geophys. Res., 116, 2011.
Rampal , P., Bouillon, S., Bergh, J., and Ólason, E.: Arctic sea-ice diffusion from observed and simulated Lagrangian trajectories, The
Cryosphere, 10, 1513–1527, 2016.
Rampal , P., Bouillon, S., Ólason, E., and Morlighem, M.: neXtSIM: A new Lagrangian sea ice model, The Cryosphere, 10, 1055–1073,
2016.
Xie , J., Bertino, L., Counillon, F., Lisæter, K. A., and Sakov, P.: Quality assessment of the TOPAZ4 reanalysis in the Arctic over the period
1991-2013, Ocean Science, 13, 123, 2017.
Thank you !

34. neXtSIM (simulation without data assimilation): RMSE ∼ 2.5km/day
TOPAZ (simulation with data assimilation): RMSE ∼ 4km/day
neXtSIM evaluation (drift)
Pointwise comparison of model vs GlobIce dataset
(winter 2007-2008)
(Rampal et al., 2016)

35. neXtSIM errors are generally lower, particularly in the winter
General positive errors in the FD in the along-drift direction e||, much smaller in neXtSIM
General smaller errors in the orthogonal-to-drift direction eL, larger in free-drift (maybe) due to a Coriolis effect
neXtSIM evaluation (role of the rheology…)
Comparison neXtSIM vs free-drift model
Forecast error with respect to IABP observations
neXtSIM
Summer
Winter
Free-Drift
Summer
Winter
(Rabatel et al., 2017 - Submitted)