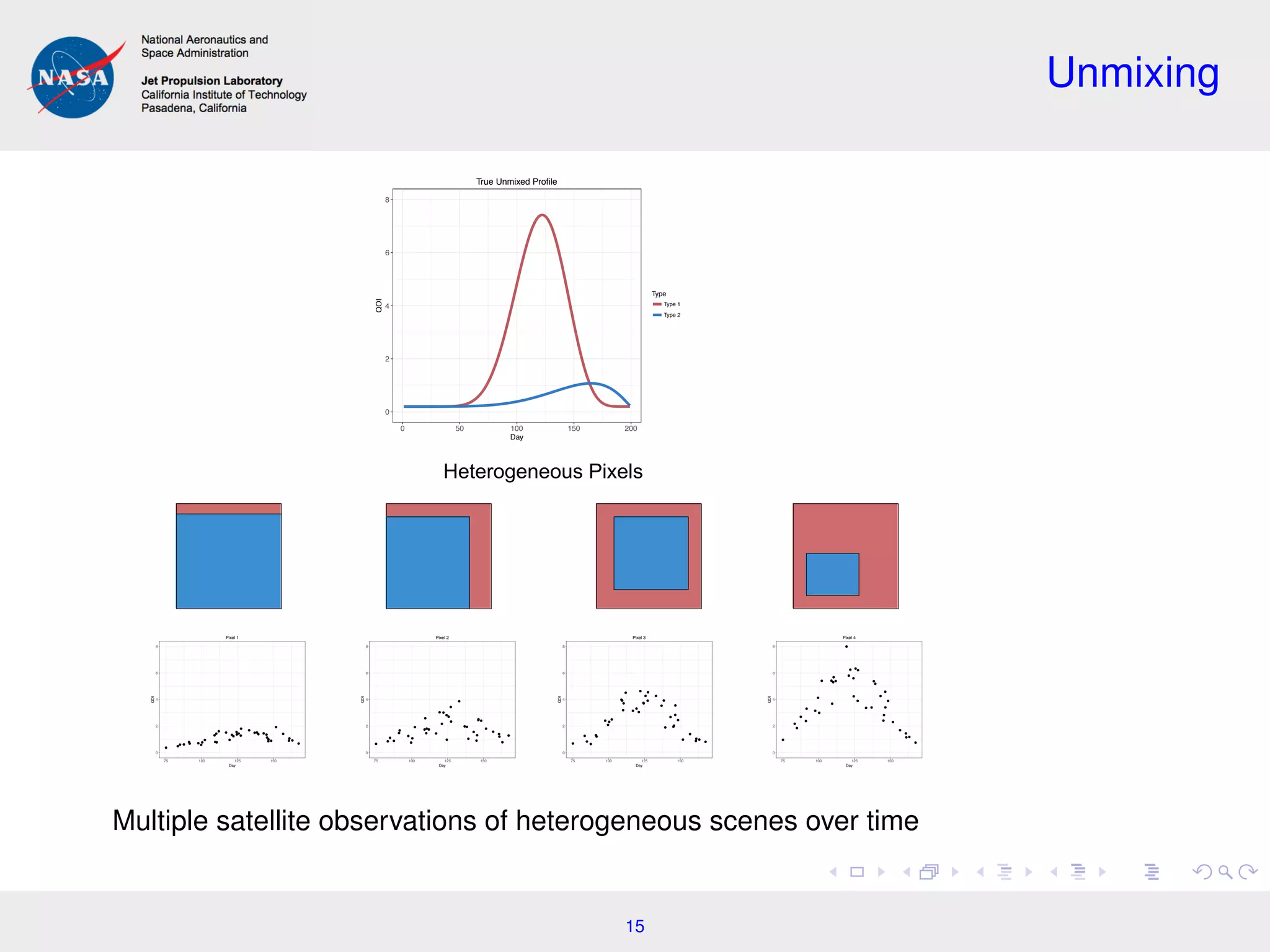
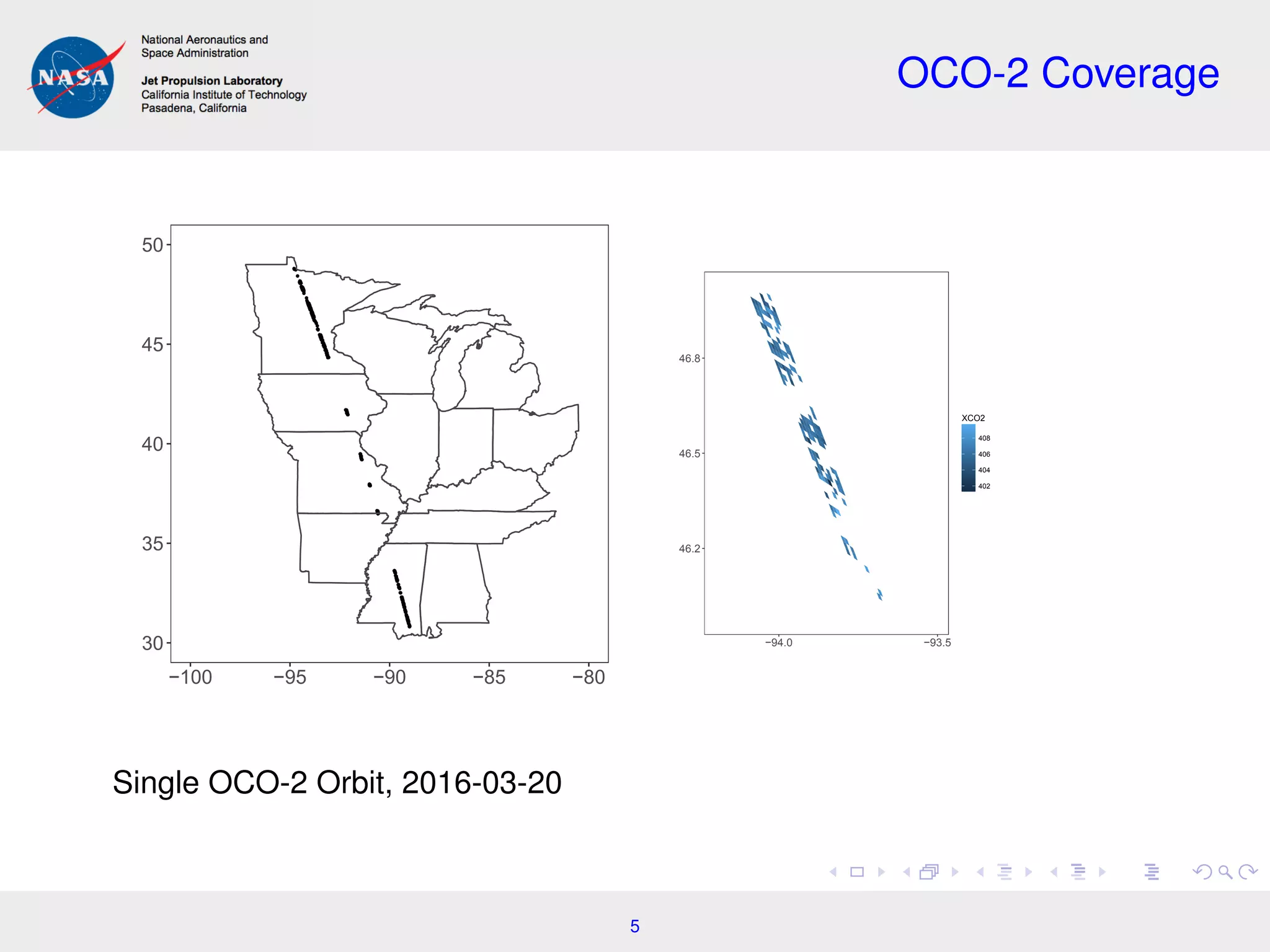
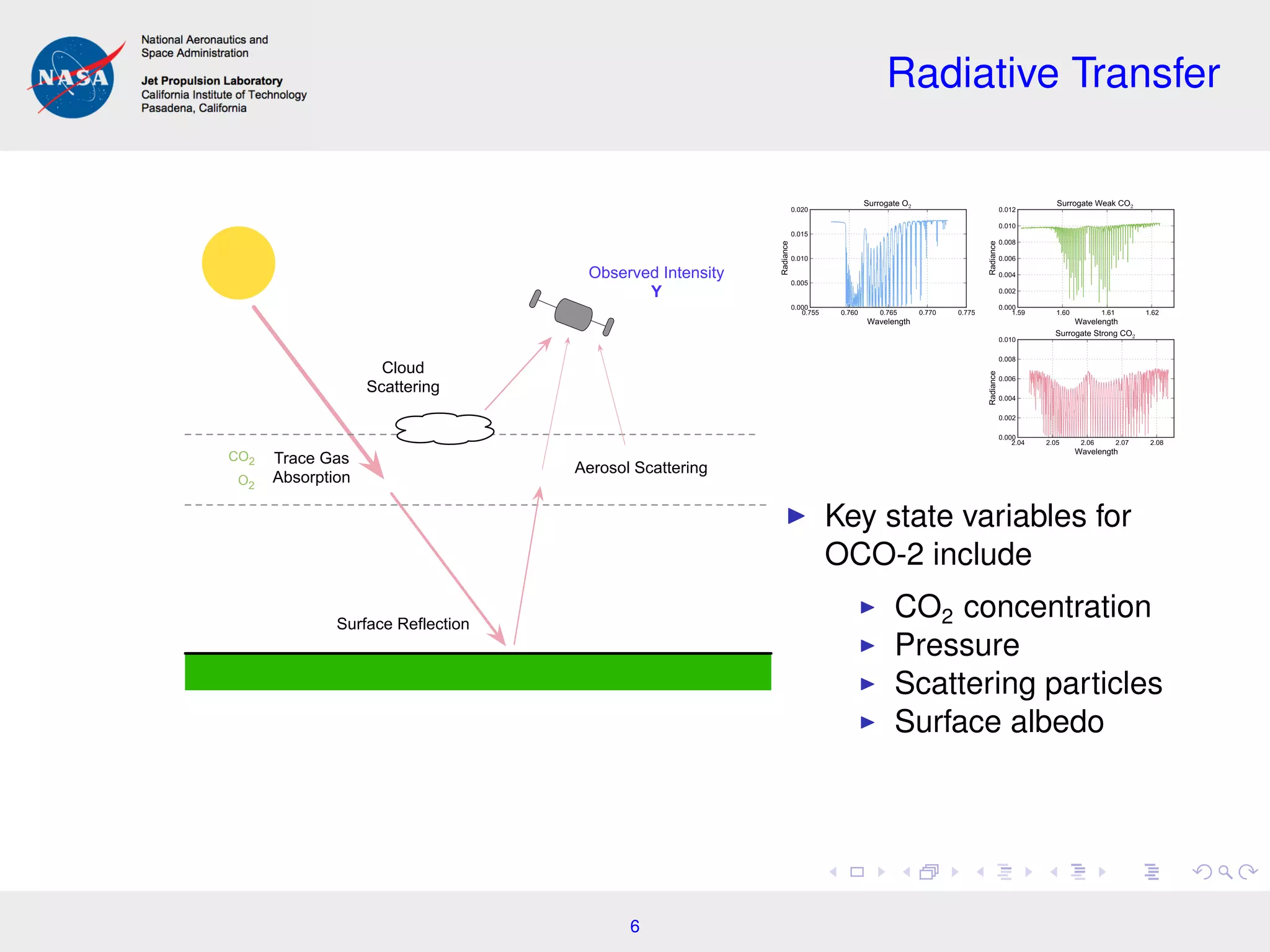
This document summarizes work on incorporating spatial dependence into atmospheric carbon dioxide retrievals from satellite data. It discusses using hierarchical Bayesian models to jointly analyze spatially correlated observations across multiple satellite footprints. This allows more precise carbon dioxide concentration estimates by borrowing strength between neighboring observations. Future work may optimize the tradeoff between precision and computational cost when analyzing larger spatial domains. The document also summarizes related work on using spatial unmixing models to estimate heterogeneous land properties like crop moisture levels from satellite imagery.

1. Incorporating Spatial Dependence in
Atmospheric Carbon Dioxide Retrievals from
High-Resolution Satellite Data
Jon Hobbs1
and the SAMSI Remote Sensing
Spatial Methodology Subgroups
1Jet Propulsion Laboratory, California Institute of Technology
February 12, 2018
1

2. Spatial Methods
Spatial Retrieval (Spatial X) Subgroup
Veronica Berrocal, Jenný Brynjarsdóttir, Jon Hobbs, Matthias Katzfuss,
Suman Majumder, Anirban Mondal
Spatial Unmixing (Spatial Y) Subgroup
Jenný Brynjarsdóttir, Jon Hobbs, Maggie Johnson, Emily Kang, Colin
Lewis-Beck, Anirban Mondal, Joon Jin Song, Zhengyuan Zhu
2

3. Spatial Retrieval
Spatial Retrieval
3

4. OCO-2
Satellite data provide a wealth of information for
geoscientists through fine space-time resolution
and extensive coverage.
Satellite-based estimates of carbon dioxide (CO2)
from a collection of satellites, including NASA’s
Orbiting Carbon Observatory-2 (OCO-2), can
provide a more comprehensive constraint on the
carbon cycle.
Remote sensing retrieval provides inference on
atmospheric state given satellite radiances. NASA
produces Level 2 data products with retrieval
results.
Reported uncertainties, or standard errors, dictate
relative weight of CO2 estimates in further
inference.
http://oco.jpl.nasa.gov
4

5. OCO-2 Coverage
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqq
qqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqq
qqqqqqqqqqqqqq
qqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqq
qqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqq
qqqq
qqqqqqqqqqqqqqqqq
qqqqq
qqqqqqqqqqqqq
qqqqq
qqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqq
q
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
q
q
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
q
qqqqqqqq
30
35
40
45
50
−100 −95 −90 −85 −80
46.2
46.5
46.8
−94.0 −93.5
402
404
406
408
XCO2
Single OCO-2 Orbit, 2016-03-20
5

6. Radiative Transfer
Trace Gas
Absorption
Surface Reflection
Aerosol Scattering
Observed Intensity
Y
Cloud
Scattering
O2
CO2
0.755 0.760 0.765 0.770 0.775
Wavelength
0.000
0.005
0.010
0.015
0.020
Radiance
Surrogate O2
1.59 1.60 1.61 1.62
Wavelength
0.000
0.002
0.004
0.006
0.008
0.010
0.012
Radiance
Surrogate Weak CO2
2.04 2.05 2.06 2.07 2.08
Wavelength
0.000
0.002
0.004
0.006
0.008
0.010
Radiance
Surrogate Strong CO2
Key state variables for
OCO-2 include
CO2 concentration
Pressure
Scattering particles
Surface albedo
6

7. Notation
The atmospheric state is represented as a random vector Xi .
A measurement vector Yi of n elements, representing radiances measured
by the instrument.
The relationship between the state and the expected response is captured
in a forward model, F(Xi , B).
A vector of forward model parameters, B, captures other quantitative
characteristics of the forward model.
A statistical model links the measurement vector, Yi , to the state vector, Xi ,
Yi = F(Xi , B) + i .
7

8. Statistical Model
Consider a hierarchical model for a single pixel/footprint,
Xi ∼ MVN (µi , Σi )
Yi |Xi , B ∼ MVN (F(Xi , B), Σ )
Σ = Var ( i )
The conditional distribution can be used for inference on the state,
−2 ln[Xi |Yi , B] = (Yi − F(Xi , B))T
Σ−1
(Yi − F(Xi , B))
+ (Xi − µi )T
Σ−1
i (Xi − µi ) + constant.
8

9. State Vector
The state vector for footprint i can be partitioned into the CO2 and non-CO2
components
Xi = Xi,a Xi,b Xi,c Xi,d
T
Xi,a =


Xi,1 : CO2 concentration at level 1
. . .
Xi,20 : CO2 concentration at level 20


Xi,b = Xi,21 : Surface pressure
Xi,c =


Xi,22 : Albedo coefficient 1
. . .
Xi,27 : Albedo coefficient 6


Xi,d =


Xi,28 : Aerosol type 1, coefficient 1
. . .
Xi,39 : Aerosol type 4, coefficient 3


Above state vector configuration for the OCO-2 surrogate model (Hobbs et
al., 2017)
9

10. Single Footprint
Primary quantity of interest, XCO2 is a pressure weighted average of the
CO2 profile,
XCO2 = hT
Xi,a
The distribution for an individual footprint is taken to be Gaussian,
Xi ∼ MVN(µi , Σi )
Σi =




Σi,aa 0 0 0
0 Σi,bb 0 0
0 0 Σi,cc 0
0 0 0 Σi,dd




10

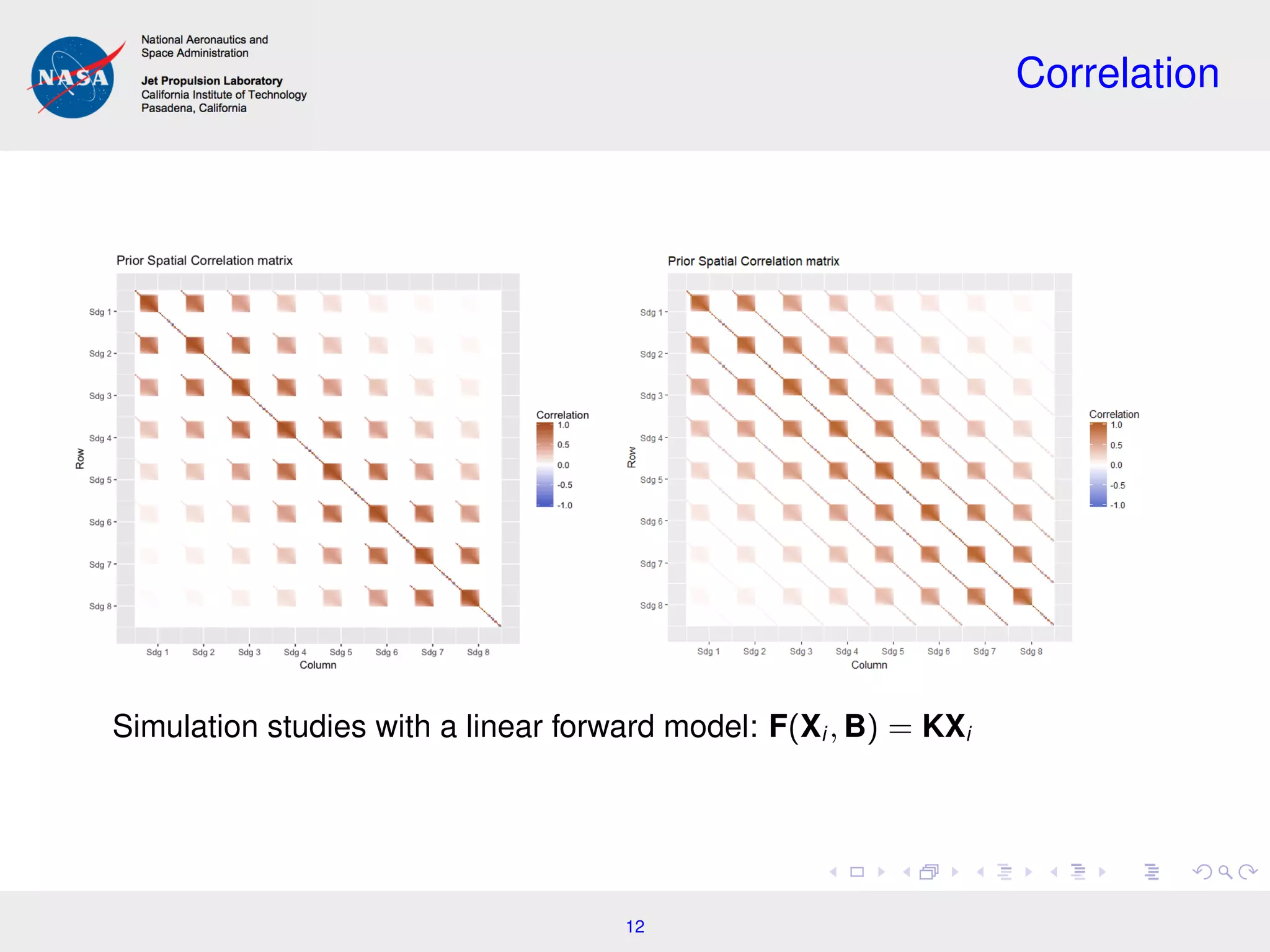
11. Spatial Case
Consider, X = [X1 X2 . . . X8] , a collection of state vectors along an
eight-footprint transect:
X1 X2 X3 X4 X5 X6 X7 X8
Joint distribution
X ∼ MVN(µ, Σ)
Cost function
−2 ln[X|Y, B] =
8
i=1
(Yi − F(Xi , B))T
Σ−1
(Yi − F(Xi , B))
+ (X − µ)T
Σ−1
(X − µ) + constant.
11

12. Correlation
Simulation studies with a linear forward model: F(Xi , B) = KXi
12

13. Discussion
Future Work
Nonlinear case with iterative optimization
Joint inference for spatial dependence parameters in Σ, (Dubovik et al.,
2011; Wang et al., 2013)
Considerations for Data Systems
Initial results suggest the joint inference yields more precise (lower
standard error) estimates of XCO2.
Precision could improve with expanded spatial domain, but
computational cost also increases.
Can the trade-off be optimized?
Nonlinear optimization
Individual likelihood evaluations can be parallelized
Spatial prior density is relatively cheap to evaluate
−2 ln[X|Y, B] =
8
i=1
(Yi − F(Xi , B))T
Σ−1
(Yi − F(Xi , B))
+ (X − µ)T
Σ−1
(X − µ) + constant.
13

14. Spatial Unmixing
Spatial Unmixing
14

15. Unmixing
0
2
4
6
8
0 50 100 150 200
Day
QOI
Type
Type 1
Type 2
True Unmixed Profile
●
●
●
●●
●
●
●
● ●
●
●
●
●
●
●●
●
●
●● ●
●
●
●
●
●
●
●
●
●
● ●
● ●
● ●
●
●
●
0
2
4
6
8
75 100 125 150
Day
QOI
Pixel 1
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
0
2
4
6
8
75 100 125 150
Day
QOI
Pixel 2
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
0
2
4
6
8
75 100 125 150
Day
QOI
Pixel 3
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
0
2
4
6
8
75 100 125 150
Day
QOI
Pixel 4
Heterogeneous Pixels
Multiple satellite observations of heterogeneous scenes over time
15

16. Unmixing
Problem Overview
An individual satellite footprint provide an aggregate view of a
heterogenous pixel/footprint
Properties of different constituents of the land
Example: moisture storage by different crops
Data from Soil Moisture Ocean Salinity (SMOS) satellite
Estimate water storage behaviors as a function of crop maturity for
corn and soybean
Considerations for Data Systems
Complex computational routines, e.g. EM algorithm, MCMC, are used for
Bayesian hierarchical models
Reference/ground data are sometimes combined with satellite data
16

17. Acknowledgments
Questions?
Jonathan.M.Hobbs@jpl.nasa.gov
Copyright 2018 California Institute of Technology, all rights reserved.
Government sponsorship acknowledged.
17

18. References
References
Dubovik, O. et al. (2011). Statistically optimized inversion algorithm for enhanced retrieval of aerosol
properties from spectral multi-angle polarimetric satellite observations. Atmos. Meas. Tech.,
4:975–1018. doi:10.5194/amt-4-975-2011.
Hobbs, J., Braverman, A., Cressie, N., Granat, R., and Gunson, M. (2017). Uncertainty quantification
for retrieving atmospheric CO2 from satellite data. SIAM/ASA J. Uncertainty Quantification,
5:956–985.
Wang, Y., Jiang, X., Yu, B., and Jiang, M. (2013). A hierarchical Bayesian approach for aerosol retrieval
using MISR data. J. Amer. Stat. Assoc., 108:483–493. doi:10.1080/01621459.2013.796834.
18