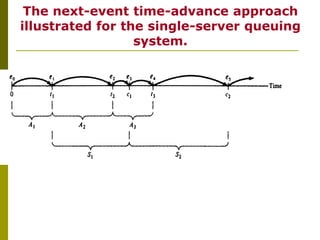
The document classifies simulation models into categories: static vs. dynamic, deterministic vs. stochastic, and continuous vs. discrete. It focuses on discrete-event simulation models, emphasizing their characteristics, like changes occurring at distinct points in time and the use of a simulation clock to track time advancements. The document also explains the next-event time advance method and provides an example related to a single-server queuing system.

1. Classification of Simulation Models
1. Static vs. Dynamic Simulation Model
• Static Simulation Model is a representation
of a system at a particular point in time
(i.e., time plays no role)
• Examples: Monte Carlo Simulation (will discuss
later)
1. Estimating the probability of winning a game in a
casino machine.
2. Estimating the value of π.
• Dynamic Simulation Model is a representation of
a system as it evolves over time
•Examples include models of a bank, a processor

2. 2. Deterministic vs. Stochastic Simulation
Models
• Deterministic Simulation Model does not
contain any probabilistic components.
• Example: a system of differential
equations representing a chemical
reaction.
• Output are also deterministic
• Stochastic Simulation models: those
having at least some random input
components.
1. Examples include Queuing models (Interarrival
times between two consecutive customers and
service times are usually random)
2. They produce output that are also random.

3. 3. Continuous vs. Discrete Simulation
Models.
Discrete Simulation models those
representing systems whose state changes at
discrete points of time.
Changes of the system occur continuously as
the time evolves

4. Discrete-event Simulation Model
•Simulation models we consider in this course are
discrete, dynamic, and stochastic. Such models are
called Discrete-Event Simulation Models
•Changes occur at a separate points of time
• i.e., The system can change only at a countable
number of points in time.
•What does it change the system state? Events
Event: is an instantaneous occurrence that changes
the state of the system Examples: Arrival of a new
customer, a Departure of a customer from a queuing
model

5. Time-Advance Mechanism
 Simulation Clock: is a variable in the simulation
model that keeps track of the current simulation
time (does not depend on the computer time)
Simulation clock
0
There are 2 approaches for advancing the simulation
clock:
1. Next-event time advance
2. Fixed-increment time advance
0 Dt 2 Dt 3 Dt 4 Dt

6. Next-Event Time Advance
 The most common used approach :
1. The simulation clock is initialized to zero.
2. Time of occurrence of future events are
determined.
3. The simulation clock is then advanced to the
time of the occurrence of the next event (the
event that is scheduled to occur first).
4. The system is updated taking in account that
the event has occurred.
5. Update the time of the occurrence of the next
events.
6. Go to step 3.
7. Repeat until a stopping criterion is satisfied.

7. Example: A single server
Queuing system
 e.g., one-operator barbershop, a cashier in a
supermarket, etc.
 Define:
 ti = time of arrival of the ith customer.
 Ai = ti – ti-1 = the interarrival time between the (i-1)st
and the ith customer.
 Si = the service time of the ith customer
 Di = the delay time in queue of the ith customer.
 ci = ti + Di + Si = departure time of the ith customer.
 ei = The time of the occurrence of the ith event.

8. The next-event time-advance approach
illustrated for the single-server queuing
system.