This document discusses floating point arithmetic. It begins by introducing the IEEE floating point standard and topics like rounding and floating point operations. It then discusses how fractional binary numbers are represented and the numerical format used in floating point, including normalized and denormalized values. Special values like infinity, NaN, positive/negative zero are also covered. The document concludes by discussing properties of floating point addition, multiplication, and how they differ from mathematical ideals due to rounding errors and special values.



![CS 213 S’01
– 5 –
class10.ppt
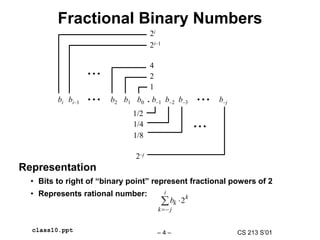
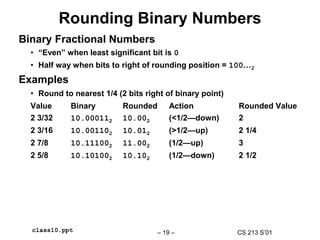
Fractional Binary Number Examples
Value Representation
5-3/4 101.112
2-7/8 10.1112
63/64 0.1111112
Observation
• Divide by 2 by shifting right
• Numbers of form 0.111111…2 just below 1.0
– Use notation 1.0 –
Limitation
• Can only exactly represent numbers of the form x/2k
• Other numbers have repeating bit representations
Value Representation
1/3 0.0101010101[01]…2
1/5 0.001100110011[0011]…2
1/10 0.0001100110011[0011]…2](https://image.slidesharecdn.com/class10-220303140323/85/Class10-5-320.jpg)

















![CS 213 S’01
– 29 –
class10.ppt
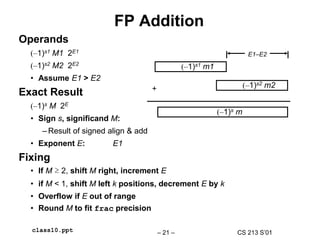
Floating Point Code Example
Compute Inner Product of Two Vectors
• Single precision arithmetic
• Scientific computing and
signal processing workhorse
float ipf (float x[],
float y[],
int n)
{
int i;
float result = 0.0;
for (i = 0; i < n; i++) {
result += x[i] * y[i];
}
return result;
}
pushl %ebp # setup
movl %esp,%ebp
pushl %ebx
movl 8(%ebp),%ebx # %ebx=&x
movl 12(%ebp),%ecx # %ecx=&y
movl 16(%ebp),%edx # %edx=n
fldz # push +0.0
xorl %eax,%eax # i=0
cmpl %edx,%eax # if i>=n done
jge .L3
.L5:
flds (%ebx,%eax,4) # push x[i]
fmuls (%ecx,%eax,4) # st(0)*=y[i]
faddp # st(1)+=st(0); pop
incl %eax # i++
cmpl %edx,%eax # if i<n repeat
jl .L5
.L3:
movl -4(%ebp),%ebx # finish
leave
ret # st(0) = result](https://image.slidesharecdn.com/class10-220303140323/85/Class10-29-320.jpg)
![CS 213 S’01
– 30 –
class10.ppt
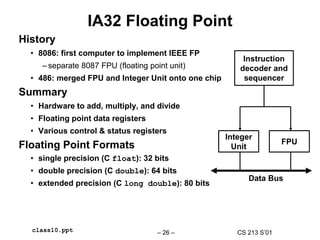
Inner product stack trace
0
st(0)
1. fldz 2. flds (%ebx,%eax,4)
0
st(0) x[0]
st(1)
3. fmuls (%ecx,%eax,4)
0
st(0) x[0]*y[0]
st(1)
4. faddp %st,%st(1)
0 + x[0]*y[0]
st(0)
5. flds (%ebx,%eax,4)
0 + x[0]*y[0]
st(0) x[1]
6. fmuls (%ecx,%eax,4)
0 + x[0]*y[0]
st(1)
x[1]*y[1]
st(0)
7. faddp %st,%st(1)
0 + x[0]*y[0] + x[1]*y[1]
st(0)
st(1)](https://image.slidesharecdn.com/class10-220303140323/85/Class10-30-320.jpg)
