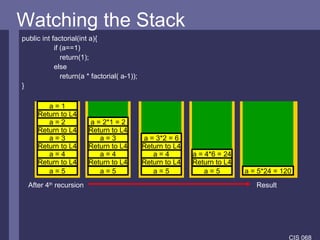
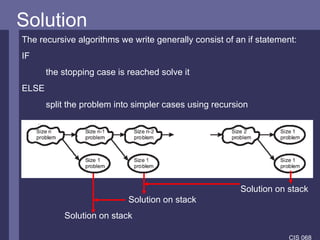
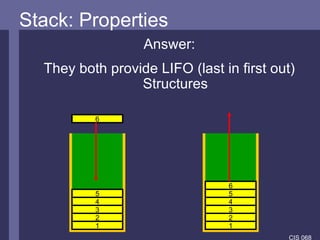
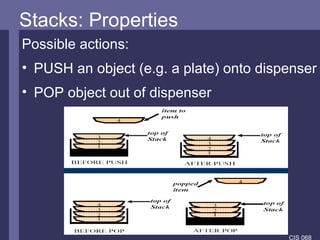
The document introduces stacks and recursion. It defines stacks as LIFO data structures and discusses how they are used in programming, particularly in method calls and the JVM. Recursion is introduced as a problem-solving technique that breaks problems down into smaller instances of the same problem. It notes recursion uses stacks to store information during method calls and provides examples of recursive algorithms and problems.

1. Welcome to CIS 068 ! Lesson 8: Stacks and Recursion

2. Overview Subjects: Stacks Structure Methods Stacks and Method – Calls Recursion Principle Recursion and Stacks Recursion vs. Iteration Examples

3. Stacks: Introduction What do these tools have in common ? Plate Dispenser PEZ ® Dispenser

4. Stack: Properties Answer: They both provide LIFO (last in first out) Structures 1 2 3 4 5 6 1 2 3 4 5 6

5. Stacks: Properties Possible actions: PUSH an object (e.g. a plate) onto dispenser POP object out of dispenser

6. Stacks: Definition Stacks are LIFO structures, providing Add Item (=PUSH) Methods Remove Item (=POP) Methods They are a simple way to build a collection No indexing necessary Size of collection must not be predefined But: extremely reduced accessibility

7. Stacks Application Areas LIFO order is desired See JVM-example on next slides ...or simply no order is necessary Lab-assignment 5: reading a collection of coordinates to draw

8. A look into the JVM Sample Code: 1 public static void main(String args[ ]){ 2 int a = 3; 3 int b = timesFive(a); 4 System.out.println(b+““); 5 } 6 Public int timesFive(int a){ 7 int b = 5; 8 int c = a * b; 9 return (c); 10 }

9. A look into the JVM Inside the JVM a stack is used to create the local variables to store the return address from a call to pass the method-parameters

10. A look into the JVM 1 public static void main(String args[ ]){ 2 int a = 3; 3 int b = timesFive(a); 4 System.out.println(b+““); 5 } 6 Public int timesFive(int a){ 7 int b = 5; 8 int c = a * b; 9 return (c); 10 } a = 3 a = 3 b Return to LINE 3 b = 5 c = 15

11. A look into the JVM ... return (c); ... a = 3 a = 3 b Return to LINE 3 b = 5 c = 15 15 a = 3 b Return to LINE 3 a = 3 b c = 15 Return to LINE 3 Temporary storage Clear Stack

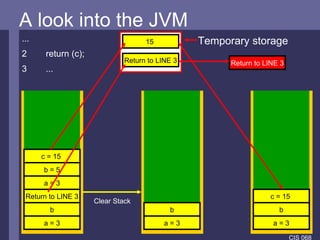
12. A look into the JVM A look into the JVM 1 public static void main(String args[ ]){ 2 int a = 3; 3 int b = timesFive(a); 4 System.out.println(b+““); 5 } a = 3 b c = 15 Temporary storage a = 3 b = 15

13. A look into the JVM A look into the JVM 1 public static void main(String args[ ]){ 2 int a = 3; 3 int b = timesFive(a); 4 System.out.println(b+““); 5 } clear stack from local variables

14. A look into the JVM A look into the JVM Important: Every call to a method creates a new set of local variables ! These Variables are created on the stack and deleted when the method returns

15. Recursion Recursion

16. Recursion Recursion Sometimes, the best way to solve a problem is by solving a smaller version of the exact same problem first Recursion is a technique that solves a problem by solving a smaller problem of the same type A procedure that is defined in terms of itself

17. Recursion Recursion When you turn that into a program, you end up with functions that call themselves: Recursive Functions

18. Recursion Recursion public int f(int a){ if (a==1) return(1); else return(a * f( a-1)); } It computes f! (factorial) What’s behind this function ?

19. Factorial Factorial: a! = 1 * 2 * 3 * ... * (a-1) * a Note: a! = a * (a-1)! remember: ...splitting up the problem into a smaller problem of the same type... a! a * (a-1)!

20. Tracing the example public int factorial(int a){ if (a==0) return(1); else return(a * factorial( a-1)); } RECURSION !

21. Watching the Stack public int factorial(int a){ if (a==1) return(1); else return(a * factorial( a-1)); } a = 5 a = 5 a = 5 Return to L4 a = 4 Return to L4 a = 4 Return to L4 a = 3 Return to L4 a = 2 Return to L4 a = 1 Initial After 1 recursion After 4 th recursion … Every call to the method creates a new set of local variables !

22. Watching the Stack public int factorial(int a){ if (a==1) return(1); else return(a * factorial( a-1)); } a = 5 Return to L4 a = 4 Return to L4 a = 3 Return to L4 a = 2 Return to L4 a = 1 After 4 th recursion a = 5 Return to L4 a = 4 Return to L4 a = 3 Return to L4 a = 2*1 = 2 a = 5 Return to L4 a = 4 Return to L4 a = 3*2 = 6 a = 5 Return to L4 a = 4*6 = 24 a = 5*24 = 120 Result

23. Properties of Recursive Functions Problems that can be solved by recursion have these characteristics: One or more stopping cases have a simple, nonrecursive solution The other cases of the problem can be reduced (using recursion) to problems that are closer to stopping cases Eventually the problem can be reduced to only stopping cases, which are relatively easy to solve Follow these steps to solve a recursive problem: Try to express the problem as a simpler version of itself Determine the stopping cases Determine the recursive steps

24. Solution The recursive algorithms we write generally consist of an if statement: IF the stopping case is reached solve it ELSE split the problem into simpler cases using recursion Solution on stack Solution on stack Solution on stack

25. Common Programming Error Recursion does not terminate properly: Stack Overflow !

26. Exercise Define a recursive solution for the following function: f(x) = x n

27. Recursion vs. Iteration You could have written the power-function iteratively, i.e. using a loop construction Where‘s the difference ?

28. Recursion vs. Iteration Iteration can be used in place of recursion An iterative algorithm uses a looping construct A recursive algorithm uses a branching structure Recursive solutions are often less efficient, in terms of both time and space , than iterative solutions Recursion can simplify the solution of a problem, often resulting in shorter, more easily understood source code (Nearly) every recursively defined problem can be solved iteratively  iterative optimization can be implemented after recursive design

29. Deciding whether to use a Recursive Function When the depth of recursive calls is relatively “shallow” The recursive version does about the same amount of work as the nonrecursive version The recursive version is shorter and simpler than the nonrecursive solution

30. Examples: Fractal Tree http://id.mind.net/~zona/mmts/geometrySection/fractals/tree/treeFractal.html

31. Examples: The 8 Queens Problem http://mossie.cs.und.ac.za/~murrellh/javademos/queens/queens.html Eight queens are to be placed on a chess board in such a way that no queen checks against any other queen

32. Review A stack is a simple LIFO datastructure used e.g. by the JVM to create local variable spaces Recursion is a divide and conquer designing technique that often provides a simple algorithmic structure Recursion can be replaced by iteration for reasons of efficiency There is a connection between recursion and the use of stacks There are interesting problems out there that can be solved by recursion