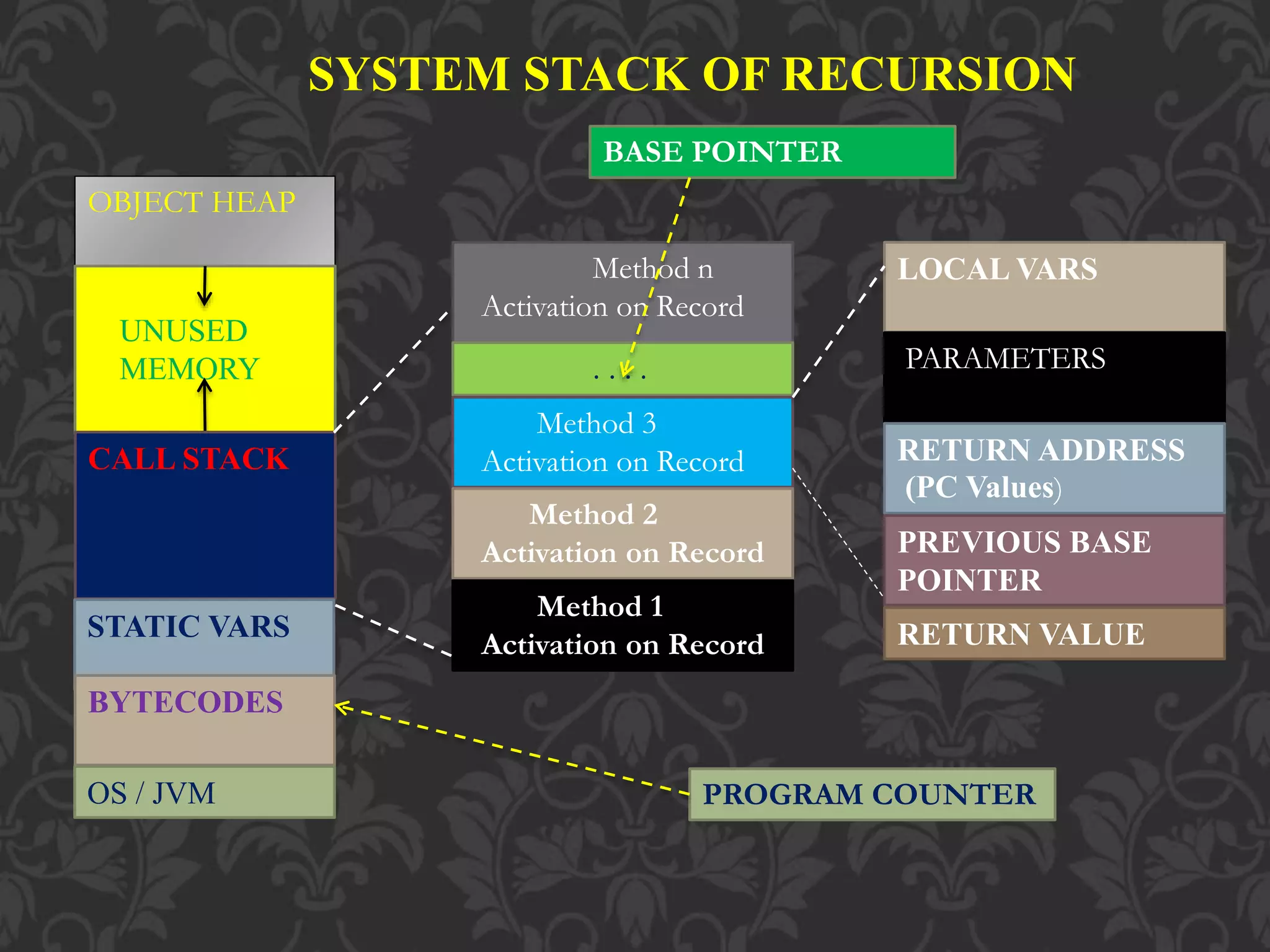
This document provides an overview of recursion, including recursive algorithms, functions, data types, and order of execution. Recursion is defined as a function calling itself, either directly or indirectly. Recursive algorithms break down a problem into smaller instances of the same problem until a base case is reached. Examples of recursive functions and data types are provided, such as factorial functions and linked lists. The order of execution for recursive functions is described, with code placed before the recursive call executing once per recursion level.

1. Advanced Data Structure
Recursion
Presented by:-A.RAVINDRA KUMAR RAO
(B.TECH (C.E))
Madanapalle Institute Of Technology & Science

2. CONTENTS
 RECURSION
 RECURSIVE ALGORITHMAS
 RECURSIVE TYPES
 RECURSIVE FUNCTIONS
 RECURSIVE DATATYPES
 ORDER OF EXECUTION
 EXAMPLE

3. RECURSION
What is recursion?
It’s when a function calls itself.
how does this happen?
When we talk about recursion, we are really talking about creating a loop.
Let’s start by looking at a basic loop.
for(int i=0; i<10;i++)
{
cout<<“the number is:”<<i<< end1;
}
Output:
the number is :0
the number is:1
the number is:2
the number is:3

4. RECURSIVE ALGORITHM
Implementation and use of Recursive Algorithms:
 space for all local, automatic (not static) variables
 space for all formal parameters
 the return address
 any other system information about the function or the function that called it.
 The function must have a selection construct which caters for the base case
 The recursive call must deal with a simpler/smaller version of the data
 Recursion uses selection construct and achieves repetition through repeated function
calls.
 Recursion has a base case.
 Any problem that can be solved recursively can be solved iteratively.

5. RECURSIVE ALGORITHM
A recursive algorithm is an algorithm which calls itself with "smaller or simpler"
input values, and which obtains the result for the current input by applying simple
operations to the returned value for the smaller input.
Example 1: Algorithm for finding the k-th even natural number
Algorithm 1: Even(positive integer k)
Input: k , a positive integer
Output: k-th even natural number (the first even being 0)
if k = 1,
then return 0;
else
return Even(k-1) + 2 .

6. RECURSIVE TYPES
Single recursion:
Recursion that only contains a single self-reference is
known as single recursion.
Example: Factorial function.
Multiple recursion:
Recursion that contains multiple self-references is known as
multiple recursion.
Ex: Fibonacci sequence
Direct recursion:
In which a function calls itself.
Ex: ƒ calls ƒ i.e. direct recursion
Indirect recursion:
Indirect recursion occurs when a function is called not by
itself but by another function that it called (either directly or
indirectly).
Ex: ƒ calls g, which calls ƒ

7. RECURSIVE TYPES
Anonymous recursion:
Recursion is usually done by explicitly calling a function by name.
However, recursion can also be done via implicitly calling a function based on
the current context, which is particularly useful for anonymous function and
is known as anonymous recursion.
Structural Recursion:
Functions that consume structured data, typically decompose their
arguments into their immediate structural components and then process
those components. If one of the immediate components belongs to the same
class of data as the input, the function is recursive.
EX: Factorial.
Generative Recursion:
Many well-known recursive algorithms generate an entirely new
piece of data from the given data and recur on it.
Ex: GCD, Binary Search

8. RECURSIVE FUNCTION
RECURSION FUNCTION:
Recursion is often seen as an efficient method of programming since it
requires the least amount of code to perform the necessary functions. However,
recursion must be incorporated carefully, since it can lead to an infinite loop if no
condition is met that will terminate the function.
MATHMATICAL FUNCTION:
In mathematics we often define a function in terms of itself.
For example: The factorial function f(n)=n!, for n is an integer, is defined as follows;
ƒ(n)={1 n≤1
{ n ƒ(n-1) n>1

9. TAIL RECURSIVE: In a tail-recursive function, none of the recursive call do
additional work after the recursive call is complete (additional work includes
printing, etc), except to return the value of the recursive call.
return rec_func( x, y ) ; // no work after recursive call, just return the
value of call
MUTUALLY RECURSIVE: For example, function f() can call function g() and
function g() can call function f(). This is still considered recursion because a
function can eventually call itself. In this case, f() indirectly calls itself.
RECURSIVE FUNCTIONS

10. FACTORIAL FUNCTION:
int Fact(int n)
{
if (n == 0)
{
return 1;
}
else
{
return n * Fact(n - 1);
}
}
RECURSIVE FUNCTION

11. RECURSIVE DATA TYPES
Inductively defined data:
An inductively defined recursive data definition is one that
specifies how to construct instances of the data.
Ex: linked list.
Co-inductively defined data type:
A co-inductive data definition is one that specifies the operations
that may be performed on a piece of data.
A co-inductive definition of infinite streams of strings
Ex: A stream of strings is an object s such that head(s) is a string,
and tail(s) is a stream of strings.

12. ORDER OF EXECUTION
In the simple case of a function calling itself only once, instructions placed before the
recursive call are executed once per recursion before any of the instructions placed
after the recursive call. The latter are executed repeatedly after the maximum
recursion has been reached.
Function 1
void recursiveFunction(int num)
{
printf("%dn", num);
if (num < 4)
recursiveFunction(num + 1);
}

13. ORDER OF EXECUTION
Function 2 with swapped lines:
void recursiveFunction(int num) {
if (num < 4)
recursiveFunction(num + 1);
printf("%dn", num);
}

14. SYSTEM STACK OF RECURSION
OBJECT HEAP
UNUSED
MEMORY
CALL STACK
STATIC VARS
BYTECODES
OS / JVM
Method n
Activation on Record
. . . .
Method 3
Activation on Record
Method 2
Activation on Record
Method 1
Activation on Record
LOCAL VARS
PARAMETERS
RETURN ADDRESS
(PC Values)
PREVIOUS BASE
POINTER
RETURN VALUE
BASE POINTER
PROGRAM COUNTER

15. REAL TIME EXAMPLE