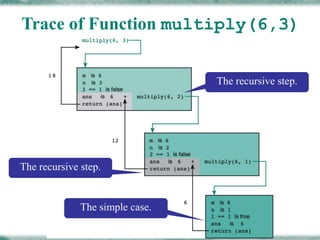
The document discusses recursion, which is a technique that solves a problem by solving smaller instances of the same problem. It provides examples of recursive functions, including factorial, combinations, multiplication, Fibonacci, and greatest common divisor (GCD). Recursive functions contain a base case with a straightforward solution and recursively define the problem in terms of smaller instances until reaching the base case. C uses a call stack to maintain the state of each recursive call.

1. Recursion
Lecturer Najia Manjur
Department of Computer Science and Engineering
Military Institute of Science and Technology

2. Recursive Function
• The recursive function is
– a kind of function that calls itself
• Recursion is a technique that solves a problem by
solving a smaller version of the same function.

3. Problems Suitable for Recursive Functions
• The problem can be reduced entirely to simple cases by
calling the recursive function.
• One or more simple cases of the problem have a
straightforward solution.
• The other cases can be redefined in terms of problems
that are closer to the simple cases.
– If this is a simple case
solve it
else
redefine the problem using recursion

4. Example of Recursion: Factorial
• Recursive implementation
int Factorial(int n)
{
if (n==0) // simple case
return 1;
else
return n * Factorial(n-1);
}

5. Trace of Recursion: Factorial
5!
5*4!
4*3!
3*2!
2*1!
1*0!
1 1
1*0!
2*1!
3*2!
4*3!
5*4!
5!
1 is returned
1*1=1 is returned
2*1=2 is returned
3*2=6 is returned
4*6=24 is returned
5*24=120 is returned

6. Coding the Factorial function (cont.)
• Iterative implementation
int Factorial(int n)
{
int fact = 1;
for(int count = 2; count <= n; count++)
fact = fact * count;
return fact;
}

7. Recursion vs. iteration
• Iteration can be used in place of recursion
– An iterative algorithm uses a looping construct
– A recursive algorithm uses a branching structure
• Recursive solutions are often less efficient, in
terms of both time and space, than iterative
solutions
• Recursion can simplify the solution of a problem,
often resulting in shorter, more easily understood
source code

8. Example of Recursion
n choose k (combinations)
• Given n things, how many different sets of
size k can be chosen?
𝑛
𝑘
= 𝑛−1
𝑘
+ 𝑛−1
𝑘−1
, 1<k<n
with base cases:
𝑛
1
= 𝑛 𝑘 = 1 , 𝑛
𝑛
= 1 (𝑘 = 𝑛)

9. int Combinations(int n, int k)
{
if(k == 1) // base case 1
return n;
else if (n == k) // base case 2
return 1;
else
return(Combinations(n-1, k) + Combinations(n-1, k-1));
}
n choose k (combinations)

11. How to write a recursive function?
• Determine the base case(s)
(the one for which you know the answer)
• Verify the algorithm
(use the "Three-Question-Method")
• Determine the general case(s)
(the one where the problem is expressed as a
smaller version of itself)

12. Three-Question Verification Method
1. The Base-Case Question:
Is there a non-recursive way out of the function,
and does the routine work correctly for this
"base" case?
2. The Smaller-Caller Question:
Does each recursive call to the function involve a
smaller case of the original problem, leading to
the base case?
3. The General-Case Question:
Assuming that the recursive call(s) work
correctly, does the whole function work
correctly?

13. Example of Recursive Function : Multiply
• We can implement the multiplication by addition.
The simple case is “m*1=m.”
The recursive step uses the following
equation: “m*n = m+m*(n-1).”

14. Trace of Function multiply(6,3)
The simple case.
The recursive step.
The recursive step.

15. Terminating Condition
• The recursive functions always contains one or
more terminating conditions.
– A condition when a recursive function is processing
a simple case instead of processing recursion.
• Without the terminating condition, the recursive
function may run forever.
– e.g., in the previous multiply function, the if
statement “if (n == 1) …” is the terminating
condition.

16. How C Maintains the Recursive Steps
• C keeps track of the values of variables by the
stack data structure.
– Stack is a data structure where the last item added is
the first item processed.
– There are two operations (push and pop) associated
with stack.
a
b
c
b
c
d
b
c
pop a push d

17. How C Maintains the Recursive Steps
• Each time a function is called, the execution
state of the caller function (e.g., parameters,
local variables, and memory address) are pushed
onto the stack.
• When the execution of the called function is
finished, the execution can be restored by
popping up the execution state from the stack.
• This is sufficient to maintain the execution of the
recursive function.
– The execution state of each recursive step are stored
and kept in order in the stack.

18. How to Trace Recursive Functions
• The recursive function is not easy to trace and to
debug.
– If there are hundreds of recursive steps, it is not useful
to set the breaking point or to trace step-by-step.
• A naïve but useful approach is inserting printing
statements and then watching the output to trace
the recursive steps.
Watch the input arguments
passed into each recursive step.

19. Recursive fibonacci Function

20. Recursive gcd Function
the greatest common divisor (GCD) of two integers m and
n can be defined recursively.
– gcd(m,n) is n if n divides m evenly;
– gcd(m,n) is gcd(n, remainder of m divided by n) otherwise.