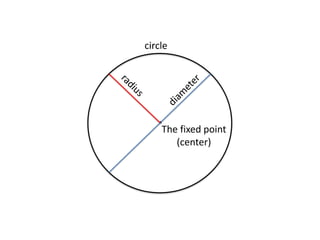
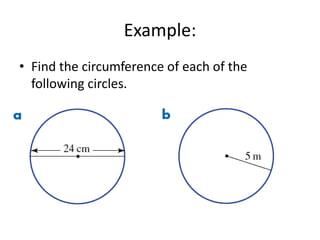
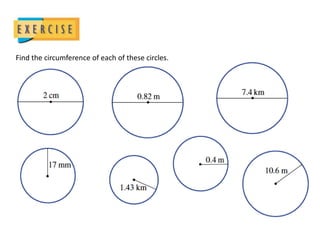
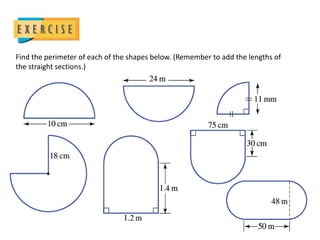
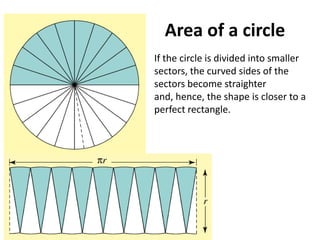
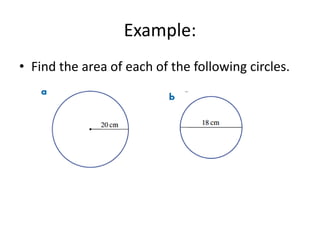
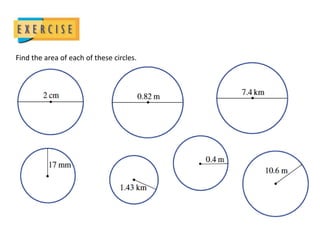
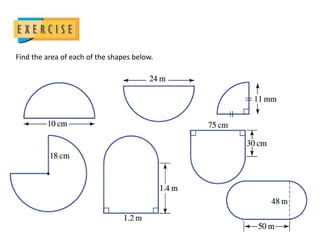
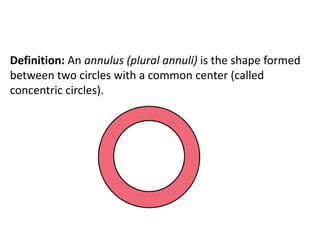
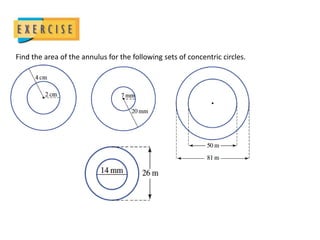
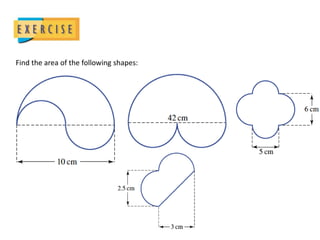
The document defines key terms related to circles such as diameter, radius, circumference, and area. It provides the formulas to calculate the circumference (C = πD) and area (A = πr^2) of a circle and includes examples of finding the circumference and area of various circles.

1. Circles

2. What is the circle?
• The set of all points those are equidistant
from a fixed point is called a circle.
• The fixed is called center of the circle.
• The line segment between two points on the
circle which is passing through the center is
called the diameter.
• The line segment between any point on the
circle and the center is called the radius (plural
radii).

3. circle
The fixed point
(center)

5. Circumference:
• The circumference is the length of the outer
boundary of a circle.

6. Finding the circumference
• The circumference of a circle is given by the
formula C = πD, where C is the circumference
and D is the diameter of a circle.
• Notice that D = 2xRadius = 2r
• π : an irrational number which is
approximately equal to 3.14.

7. Example:
• Find the circumference of each of the
following circles.

8. Find the circumference of each of these circles.

9. Find the perimeter of each of the shapes below. (Remember to add the lengths of
the straight sections.)

10. A scooter tire has a diameter of 32 cm. What is the perimeter of the tire?
Find the circumference of the Ferris wheel shown below.

12. Area of a circle
If the circle is divided into smaller
sectors, the curved sides of the
sectors become straighter
and, hence, the shape is closer to a
perfect rectangle.

13. Finding the area of a circle
• The area of a circle, A, can be found using the
formula A = π r2 , where π is a constant with a
value of approximately 3.14 and r is the radius
of the circle.

14. Example:
• Find the area of each of the following circles.

15. Find the area of each of these circles.

16. Find the area of each of the shapes below.

17. Definition: An annulus (plural annuli) is the shape formed
between two circles with a common center (called
concentric circles).

18. Find the area of the annulus for the following sets of concentric circles.

19. Find the area of the following shapes: