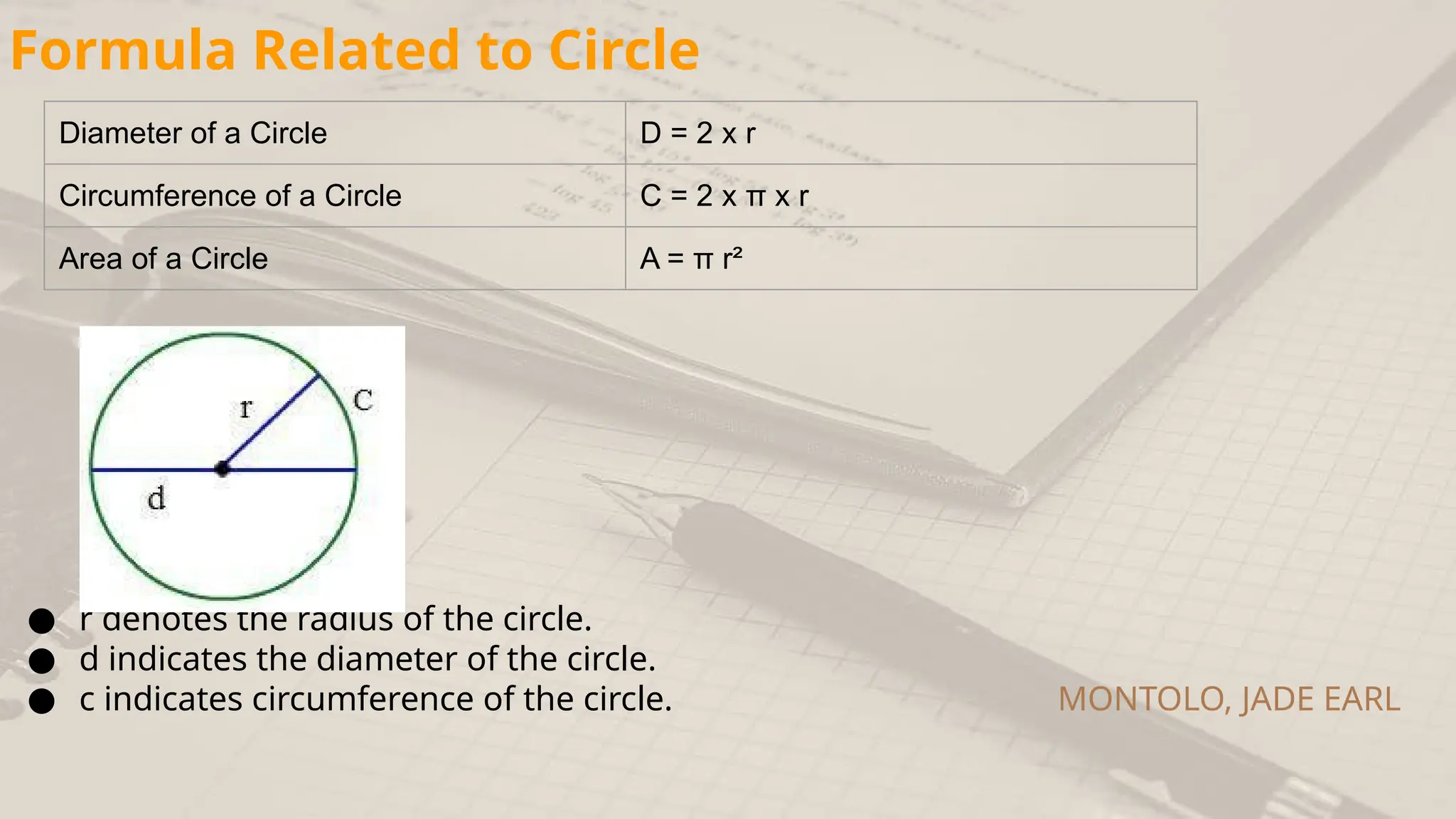
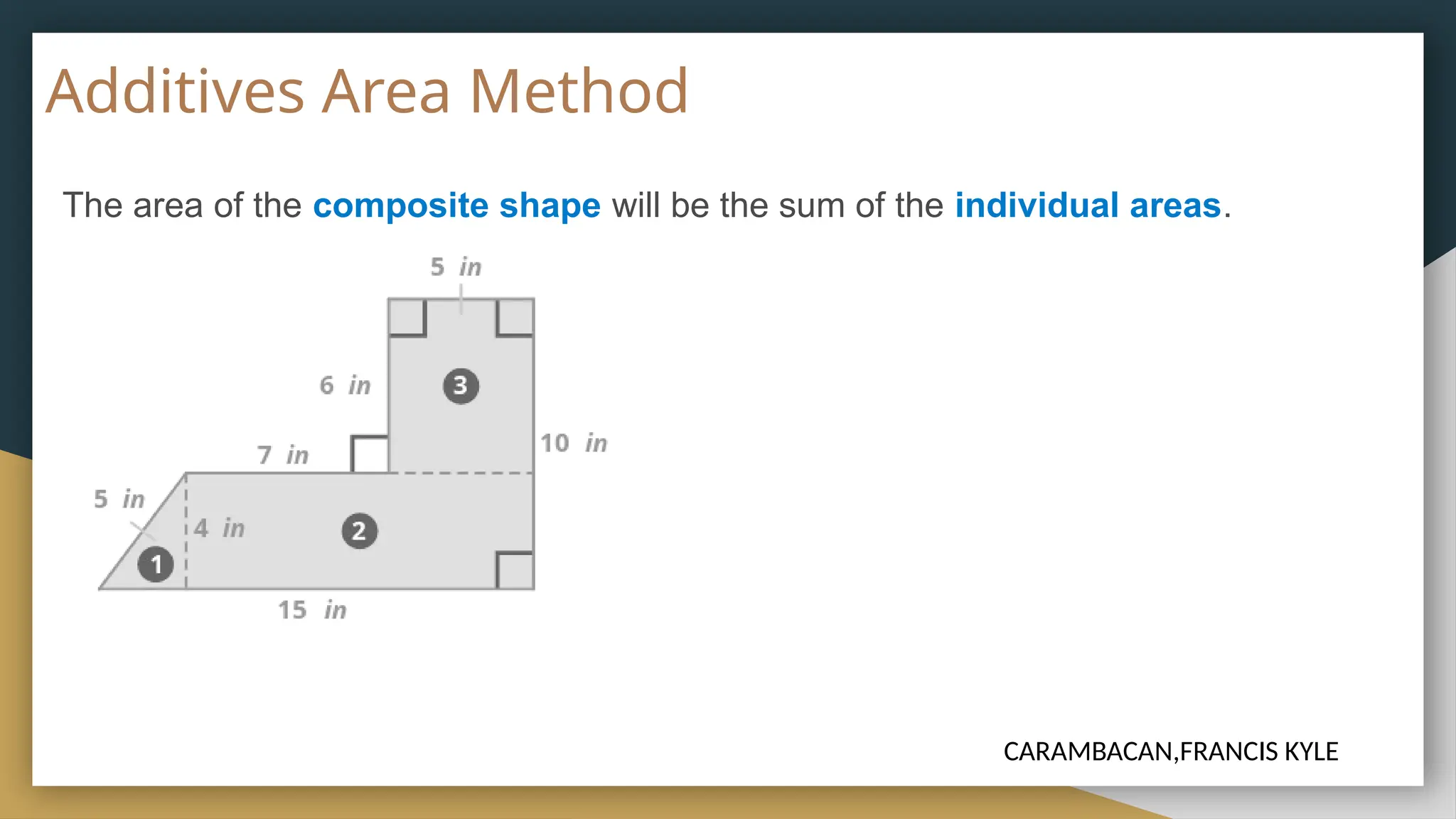
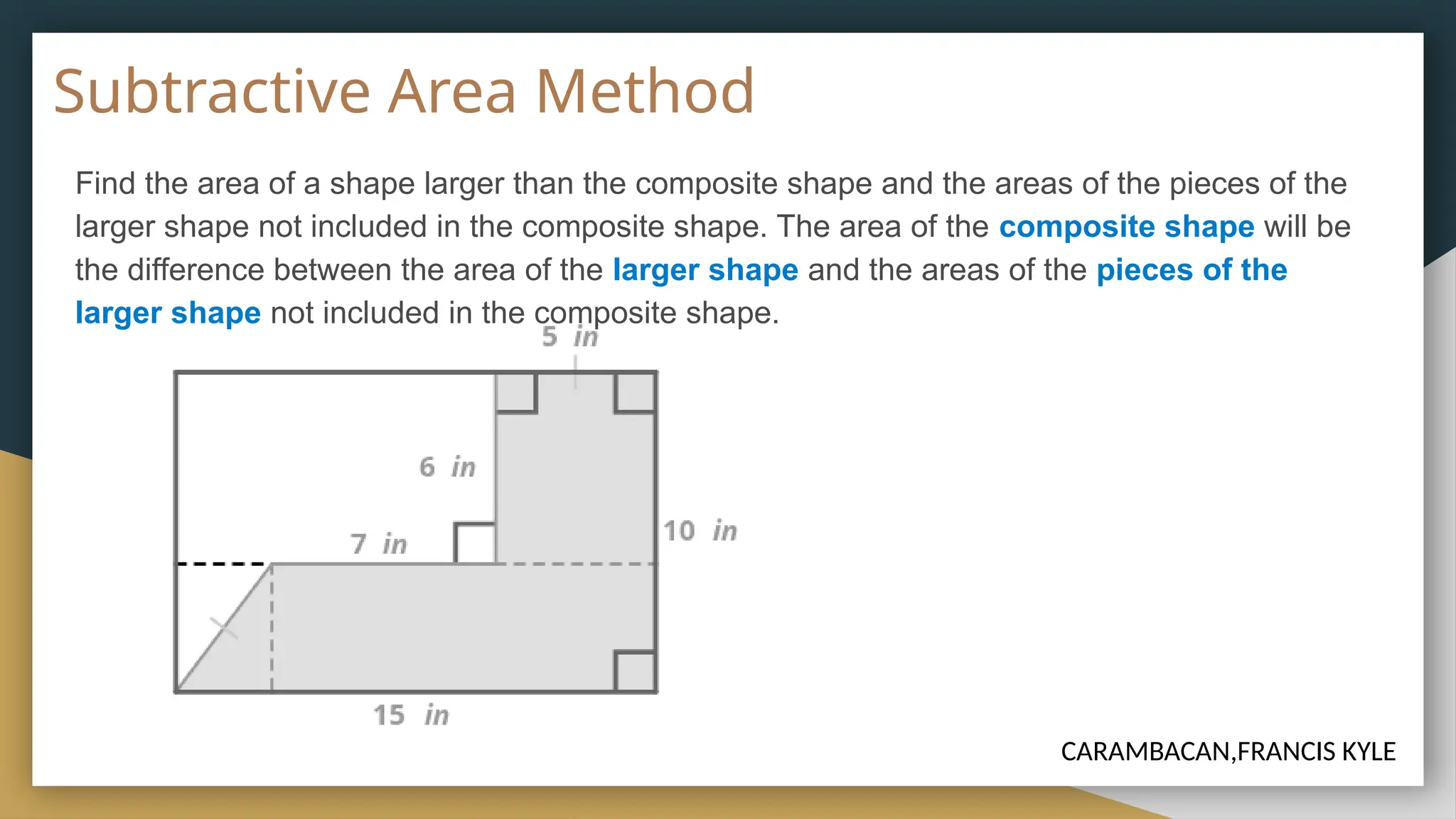
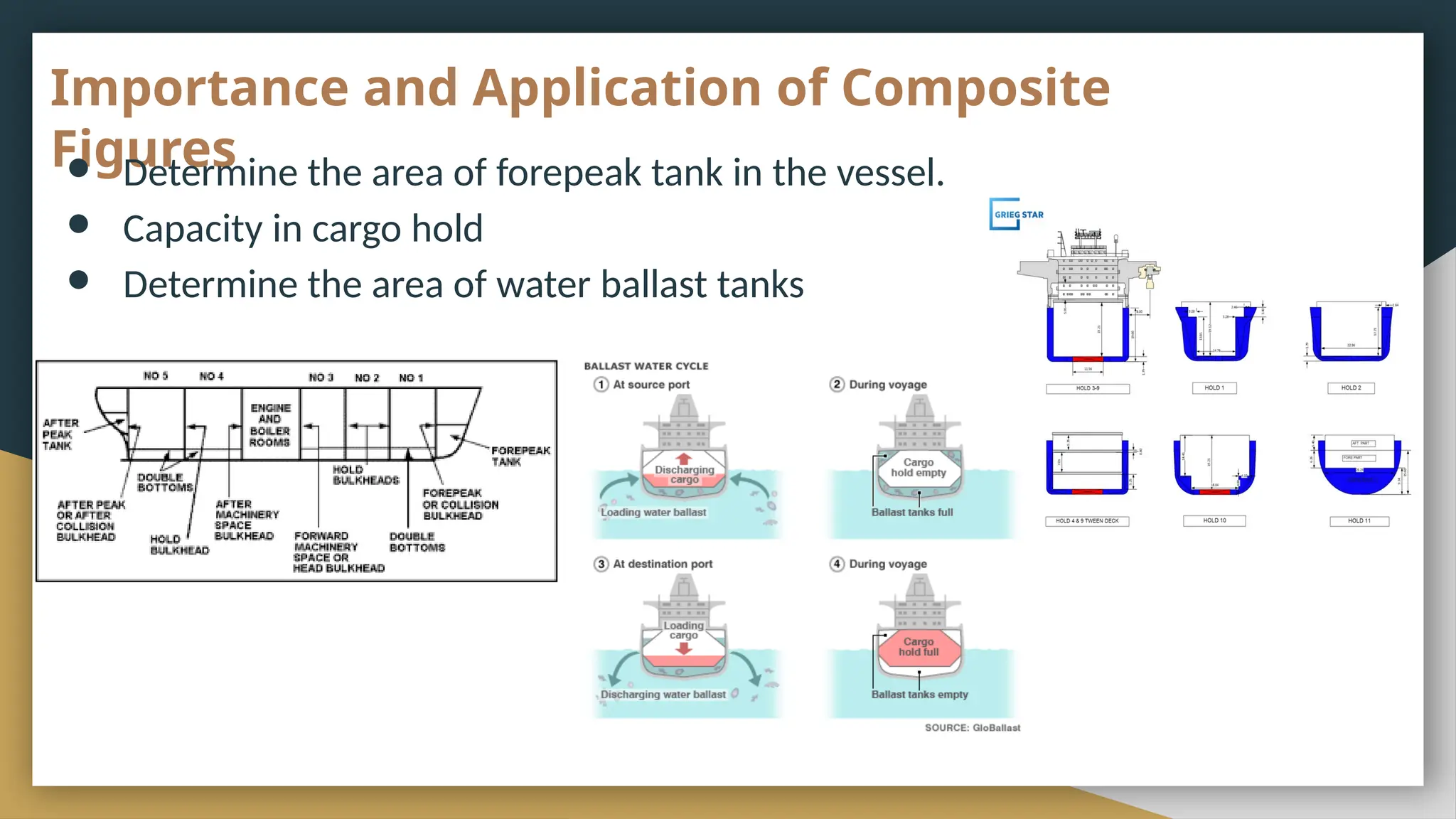
The document covers the properties and mathematical principles related to circles, including definitions, formulas for diameter, circumference, and area, as well as examples for practical calculation. It also discusses composite figures, outlining methods for calculating their areas through additive and subtractive approaches. The historical and etymological context of circles is presented, linking their significance to geometry and modern machinery.

1. Solid Mensuration
“CIRCLE AND COMPOSITE
FIGURES
Group 4
BARICUATRO,DEN MCKLEINT B.
CARAMBACAN,FRANCIS KYLE
DE ARCE, GOERGE
IGOT, AGUIDO
MONTOLO, JADE EARL
RIVERA, MYLES ANDRE O.
TECSON,STREAM LLYOD

2. OBJECTIVES OF A
CIRCLE

3. ● identify the radius, diameter, circumference, and center of
a circle,
● understand the relationship between the radius and the
diameter,
● measure parts of a circle.
BARICUATRO,DEN MCKLEINT B.

4. HISTORY
RIVERA, MYLES ANDRE O.

5. The word circle derives from the Greek
κίρκος/κύκλος (kirkos/kuklos), itself a
metathesis of the Homeric Greek κρίκος
(krikos), meaning "hoop" or "ring". The
origins of the words circus and circuit are
closely related.
RIVERA,MYLES ANDRE O.

6. The circle has been known since before the beginning of recorded history.
Natural circles would have been observed, such as the Moon, Sun, and a
short plant stalk blowing in the wind on sand, which forms a circle shape in
the sand. The circle is the basis for the wheel, which, with related inventions
such as gears, makes much of modern machinery possible. In mathematics,
the study of the circle has helped inspire the development of geometry,
astronomy and calculus.
RIVERA,MYLES ANDRE O.

7. Early science, particularly geometry and
astrology and astronomy, was connected to the divine
for most medieval scholars, and many believed that
there was something intrinsically "divine" or "perfect"
that could be found in circles
RIVERA,MYLES ANDRE O.

8. DEFINITION AND
IMPORTANT TERMS
RIVERA, MYLES ANDRE O.

9. Definition for a circle is a closed two-dimensional
figure in which the set of all the points in the plane
is equidistant from a given point called “centre”.
Every line that passes through the circle forms the
line of reflection symmetry. Also, it has rotational
symmetry around the centre for every angle.
REVIRA,MYLES ANDRE O.

10. The word ‘circle’ is derived from a Greek word that
means ‘hoop’ or ‘ring.’ In geometry, a circle is
defined as a closed two-dimensional figure in which
the set of all the points in the plane is equidistant
from a given point called “center.”
REVIRA, MYLES ANDRE O.

11. Formula Related to Circle
● r denotes the radius of the circle.
● d indicates the diameter of the circle.
● c indicates circumference of the circle. MONTOLO, JADE EARL
Diameter of a Circle D = 2 x r
Circumference of a Circle C = 2 x π x r
Area of a Circle A = π r²

12. Diameter of a Circle
The diameter of a circle is a line segment that passes through the center of the circle and with endpoints that lie on
the circumference of a circle. The diameter is also known as the longest chord of the circle and is twice the length of
the radius. The diameter is measured from one end of the circle to a point on the other end of the circle, passing
through the center. The diameter is denoted by the letter D. There can be an infinite number of diameters where the
length of each diameter of the circle is length.
● Diameter = Circumference/π (used when the circumference is given)
● Diameter = Radius × 2 (used when the radius is given)
● Diameter = 2√(Area/π) (used when the area of the circle is given)
IGOT, AGUIDO

13. Example of Diameter
1. Example 3: Find the diameter of a circle if its circumference is 88 cm.
Solution: If the circumference is given, we can find the diameter of a
circle using the following formula:
Diameter = Circumference/π
After substituting the value of circumference = 88 cm, and π = 3.14, we
get, Diameter = Circumference/π
Diameter = 88/3.14
= 28.02 cm
Therefore, the diameter of the circle is 28.02 cm.
IGOT,AGUIDO

14. Circumference of a Circle
The circumference of a circle is its boundary. In other words, when we measure the boundary or the
distance around the circle, that measure is called the circumference and it is expressed in units of length
like centimeters, meters, or kilometers. The circumference of a circle has three most important elements
namely, the center, the diameter, and the radius.
● r = radius of the circle.
● D = diameter of the circle.
● π = Pi with the value approximated to 3.14159 or 22/7.
IGOT,AGUIDO

15. Example of Circumference
1. Example 1: The circumference of a wheel is 540 cm. Find its radius and
diameter.
Solution:
Given, the Circumference of the wheel = 540 cm.
Circumference of a circle formula = 2πr
Let us substitute the given value of the circumference in the formula to find the
radius.
540 = 2πr
540 = 2 × 22/7 × r
r = 85.9 cm
Diameter = 2r
Diameter = 2 × 85.9
Therefore, the radius is 85.9 cm, and the diameter is 171.8 cm.
IGOT,AGUIDO

16. Area of a Circle
The area of a circle can be calculated in intermediate steps from the diameter, and the circumference of a
circle. From the diameter and the circumference, we can find the radius and then find the area of a circle.
But these formulae provide the shortest method to find the area of a circle. Suppose a circle has a radius 'r'
then the area of circle = πr2
or πd2
/4 in square units, where π = 22/7 or 3.14, and d is the diameter.
Area of a circle, A = πr2
square units
Circumference / Perimeter = 2πr units
Area of a circle can be calculated by using the formulas:
● Area = π × r2
, where 'r' is the radius.
● Area = (π/4) × d2
, where 'd' is the diameter.
● Area = C2
/4π, where 'C' is the circumference.
IGOT, AGUIDO

17. Example of Area of a Circle
Example 1: If the length of the radius of a circle is 4 units. Calculate its area.
Solution:
Radius(r) = 4 units(given)
Using the formula for the circle's area,
Area of a Circle = πr2
Put the values,
A = π42
A =π × 16
A = 16π ≈ 50.27
IGOT,AGUIDO

18. COMPOSITE FIGURES
BARICUATRO,DEN MCKLEINT B.

19. OBJECTIVES
● Find the areas of composite figures where two or
more shapes have been composed together,
● Find the areas of composite figures where one or
more shape is taken out of another shape.
BARICUATRO,DEN MCKLEINT B.

20. HISTORY
Made uf of distinct part or elements “ c, 1400, from old french composite from latin
compositus “placed together”, past participle of componere’ to put together, to collect a
whole from several parts , “ from com “,together”
CARAMBACAN, FRANCIS KYLE

21. COMPOSITE FIGURES
● a shape composed of a combination of other shapes.
● composite figures are often split into their component shapes to
calculate area.
● The two general methods to determine the area of a composite
shape, we could call them;
Additives area methon
Subtractive area methon
CARAMBACAN,FRANCIS KYLE

22. Additives Area Method
The area of the composite shape will be the sum of the individual areas.
CARAMBACAN,FRANCIS KYLE

23. Subtractive Area Method
Find the area of a shape larger than the composite shape and the areas of the pieces of the
larger shape not included in the composite shape. The area of the composite shape will be
the difference between the area of the larger shape and the areas of the pieces of the
larger shape not included in the composite shape.
CARAMBACAN,FRANCIS KYLE

24. Examples of
Composite Figures
CARAMBACAN, FRANCIS KYLE

25. CARAMBACAN, FRANCIS KYLE

26. CARAMBACAN,FRANCIS KYLE

27. CARAMBACAN, FRANCIS KYLE

28. Importance and Application of Composite
Figures
● Determine the area of forepeak tank in the vessel.
● Capacity in cargo hold
● Determine the area of water ballast tanks

29. REFERENCE
TECSON, STREAM LLYOD

30. https://www.wikihow.com/Calculate-the-Area-of-a-Circle?amp=1
https://www.
cuemath.com/measurement/area-of-composite-shapes/
https://byjus.com/circle-formula/
https://www.cuemath.com/geometry/area-of-a-circle/