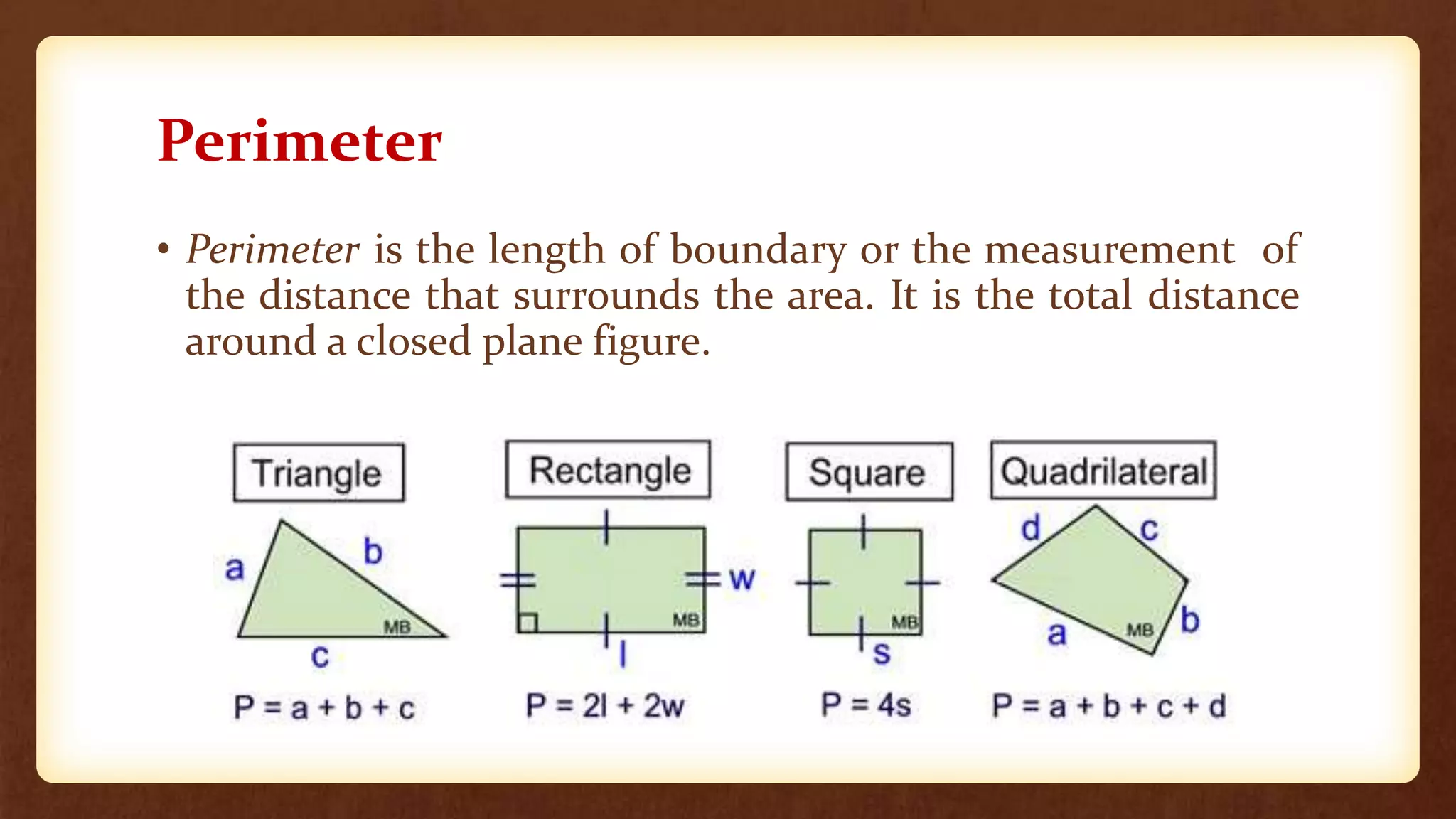
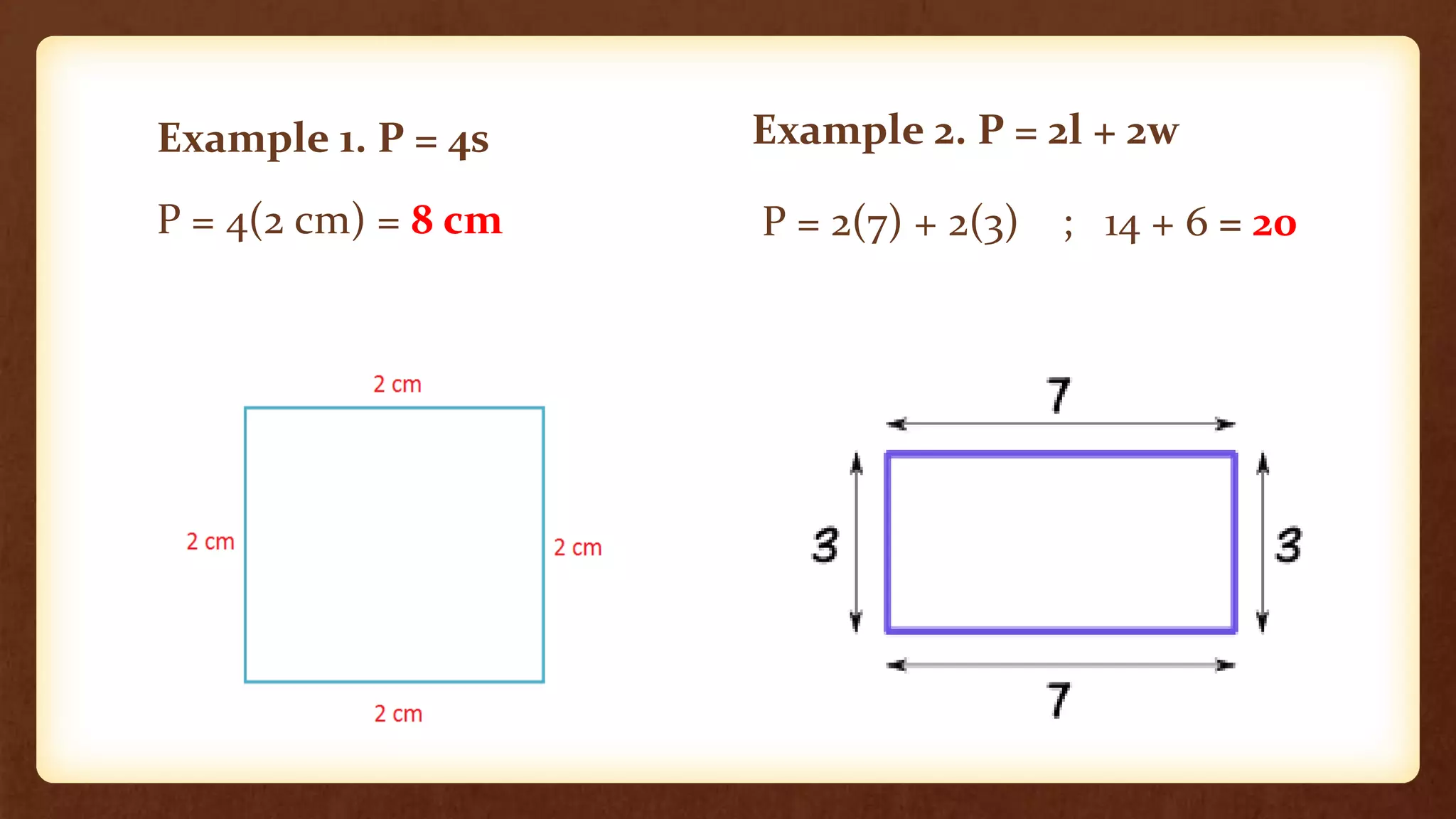
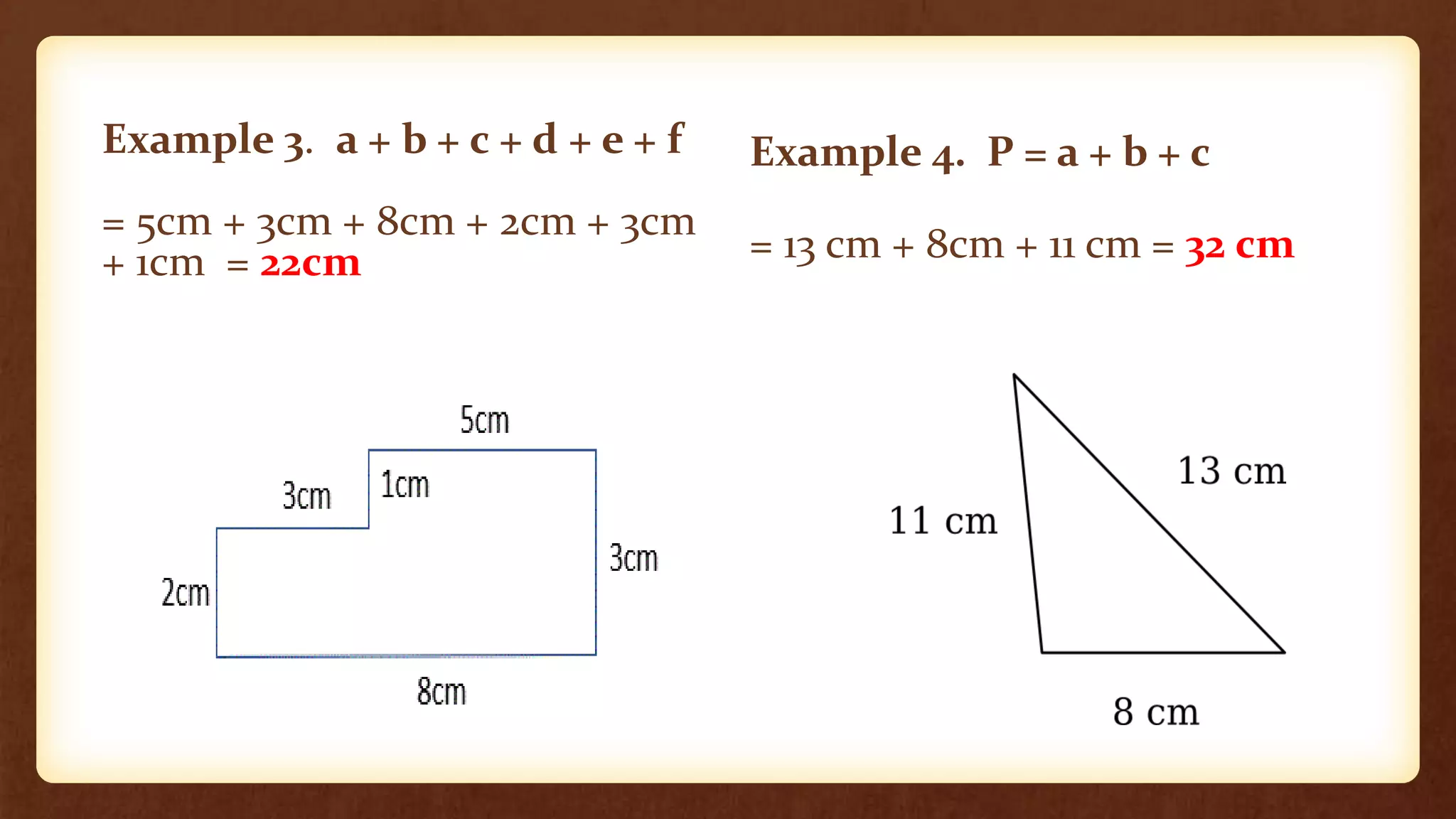
- Perimeter is the distance around a closed plane figure, while circumference is the distance around a circle. The perimeter/circumference is found using formulas involving the sides/radius and diameter. - Radius is half the diameter and measures the distance from the center of a circle to its edge, while diameter passes through the center and has endpoints on the circle, measuring twice the radius. 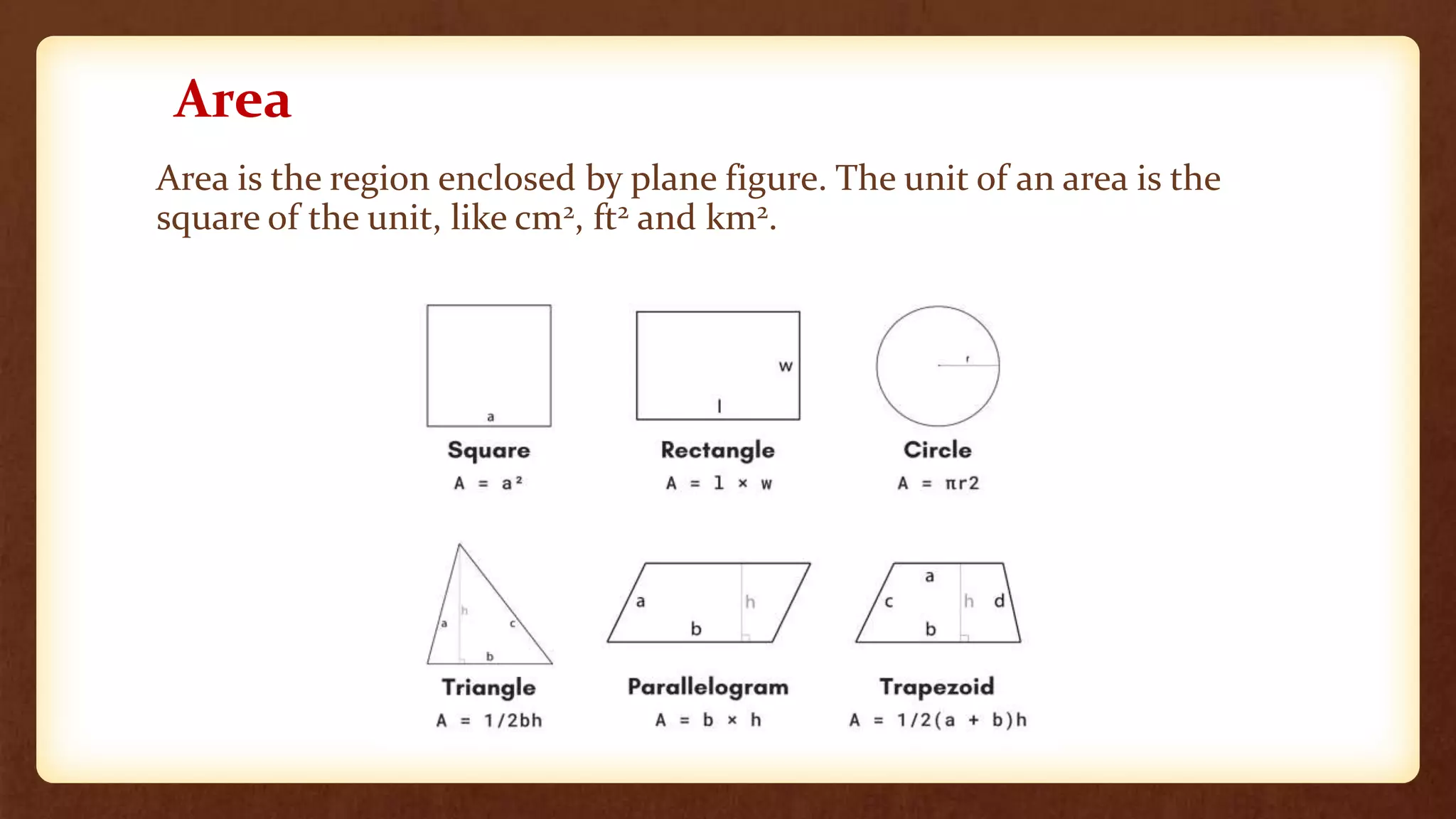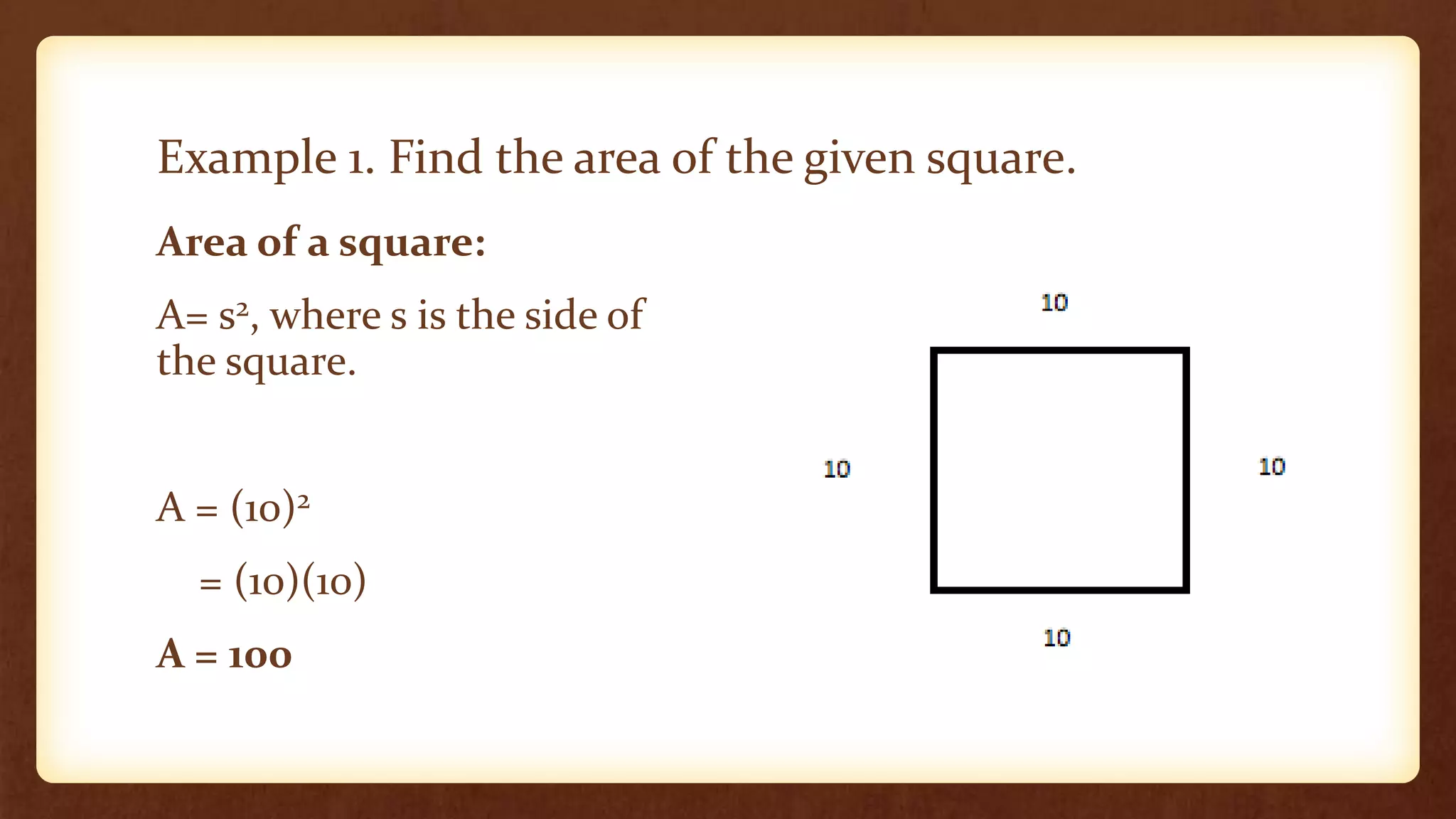- Area formulas are used to find the space enclosed by different shapes, such as squares using side length and rectangles using length and width.

2. Perimeter
• Perimeter is the length of boundary or the measurement of
the distance that surrounds the area. It is the total distance
around a closed plane figure.

3. Example 1. P = 4s
P = 4(2 cm) = 8 cm
Example 2. P = 2l + 2w
P = 2(7) + 2(3) ; 14 + 6 = 20

4. Example 3. a + b + c + d + e + f
= 5cm + 3cm + 8cm + 2cm + 3cm
+ 1cm = 22cm
Example 4. P = a + b + c
= 13 cm + 8cm + 11 cm = 32 cm

5. Example 5. a + b + c
= 3 cm + 6 cm + 8 cm = 17 cm
Example 6. equilateral
triangle = (all sides are equal)
P = 3s = 3(18 cm) = 54 cm

6. Circumference
• Circumference is the distance around a circle. It is the
perimeter of a circle.
To solve the circumference of a circle, use the following
formula:
C = 2𝜋r or C = 𝜋d
where r= radius and d = diameter.
Pi = 3.1416

7. • Radius is the distance from the center
of the circle to the point on the circle.
It measured one-half of a diameter.
• Diameter is the segment that passes
through the center of a circle and
whose endpoints lie on the circle. It
measured twice of the radius.

8. Example 1. C = 2(3.14)(8cm)

9. Example 2. The radius of a circle is 5 cm. Find the
circumference.
C = 2𝜋r
C = 2(3.14)(5cm)
C = 31.4 cm

10. Example 3. The circumference of a circle is 12.57 cm.
What is the radius?
Solution:
To find radius we have,
C = 2𝜋r
𝐶
2𝜋
= r
so, r =
𝐶
2𝜋
r =
12.57 𝑐𝑚
2(3.14)
r =
12.27 𝑐𝑚
6.28
r = 2 cm

11. Area
Area is the region enclosed by plane figure. The unit of an area is the
square of the unit, like cm2, ft2 and km2.

12. Example 1. Find the area of the given square.
Area of a square:
A= s2, where s is the side of
the square.
A = (10)2
= (10)(10)
A = 100

13. Example 2. Find the area of a rectangle whose length is
12 cm and the width is 7 cm.
Area of a rectangle = lw
A = lw
= (12cm)(7cm)
A = 84 cm2