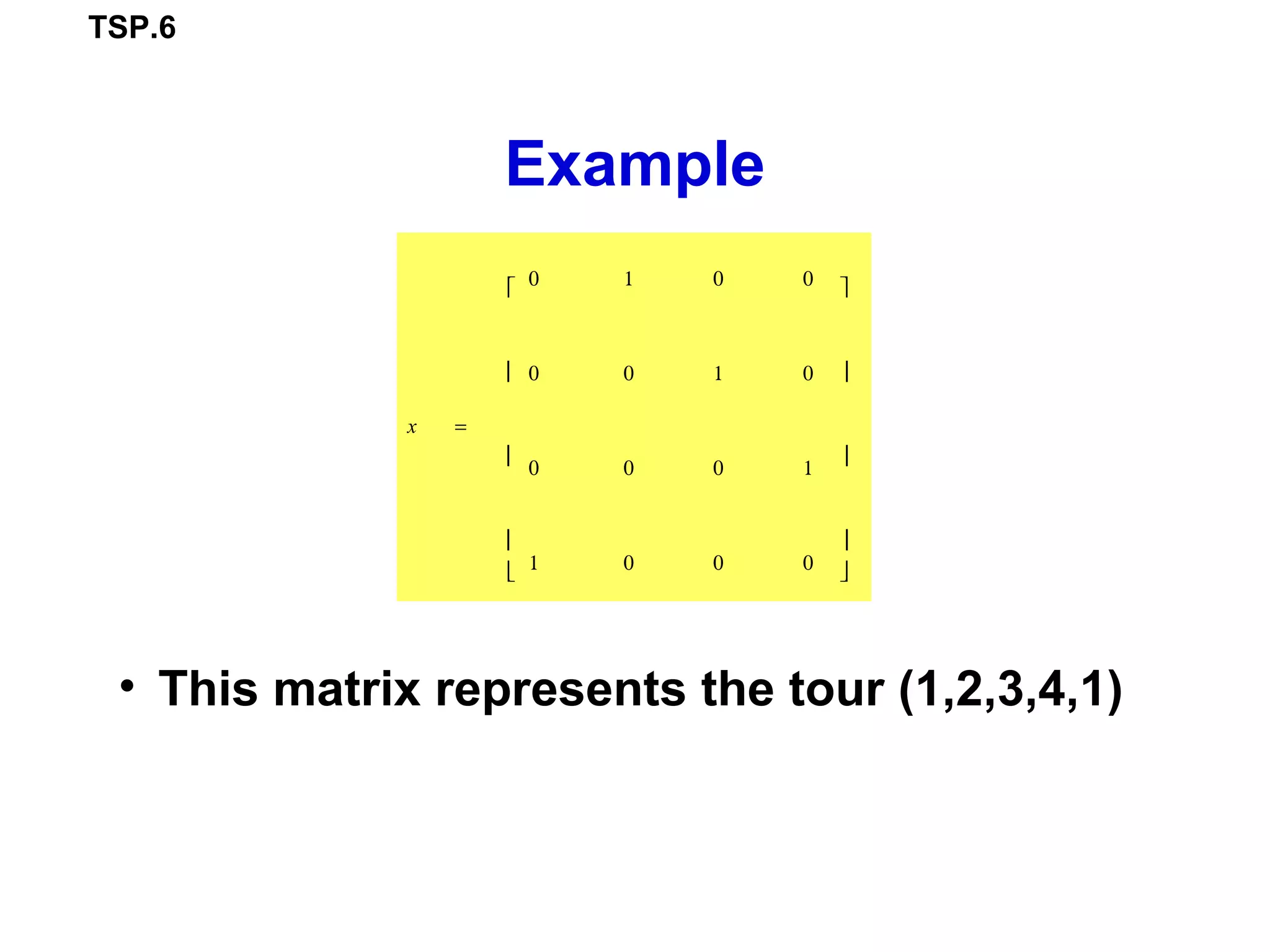
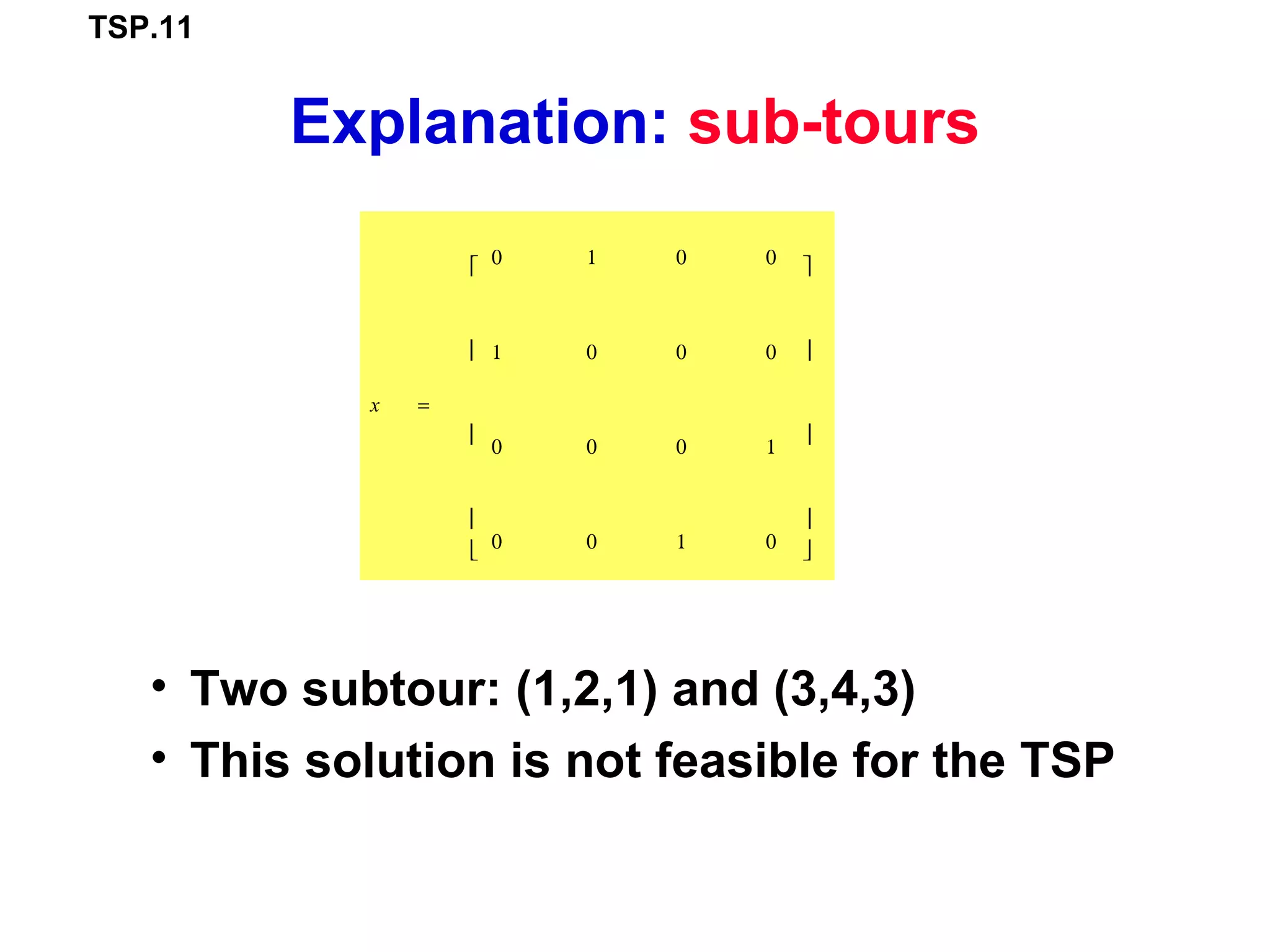
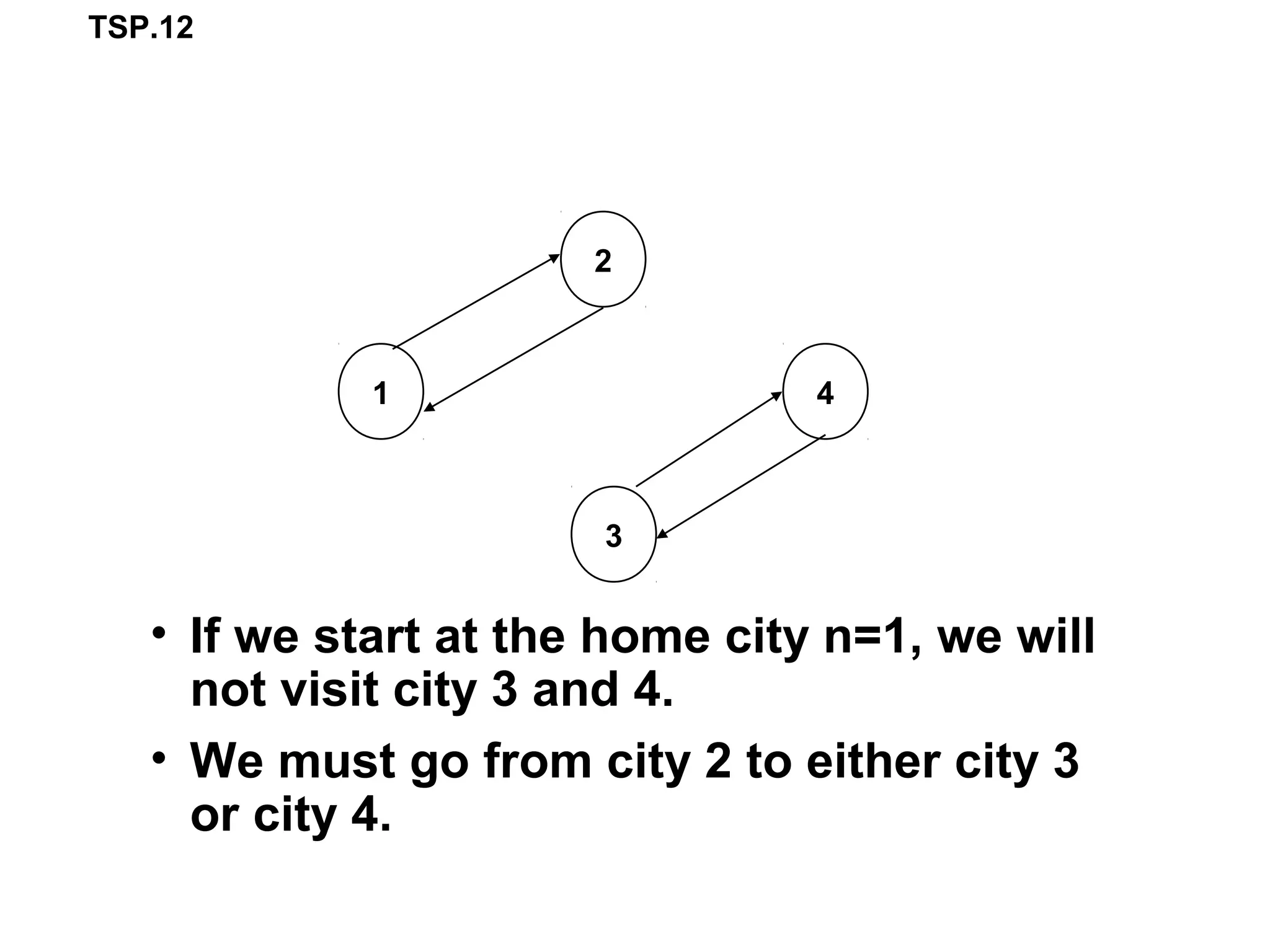
The document describes the travelling salesperson problem (TSP) and different approaches to solve it, including linear programming (LP) and dynamic programming (DP). It presents two LP formulations - one using a boolean decision variable matrix and constraints, and another using decision variables to represent the tour order. It also provides a DP formulation that recursively calculates the shortest tour length between subsets of remaining cities. An example problem is worked through step-by-step to demonstrate the DP approach.

1. TSP.1
9.4
Travelling Salesperson Problem
(TSP)
• Very famous problem
• Many practical applications
• Very easy to describe
• Very difficult to solve (Curse of Dimensionality)
• We shall consider the dynamic
programming (DP) approach
• Other approaches: see 620-362

2. TSP.2
Problem Formulation
• There are many ways to describe this
problem.
• We shall consider the following:
– English version
– Linear Programming oriented version
– Linear Programming Free version
– Dynamic programming version

3. TSP.3
English Version
• You are given a set of n cities
• You are given the distances between
the cities
• You start and terminate your tour at
your home city
• You must visit each other city exactly
once.
• Your mission is to determine the
shortest tour.

4. TSP.4
Maths versions
• We shall consider two Maths Version
• The first is LP-based
• The second is LP-free
• The first version dominates the OR
literature

5. TSP.5
TSP Version 1 (LP)
• Decision variable:
A boolean matrix x interpreted as
follows:
x(i,j):= 1, iff we go from city i to city j.
x(i,j) := 0, otherwise

6. TSP.6
Example
• This matrix represents the tour (1,2,3,4,1)
x =
0 1 0 0
0 0 1 0
0 0 0 1
1 0 0 0











7. TSP.7
Objective function
• d(i,j) = (direct) distance between city i and
city j.
z = ξ ( ι , ϕ ) δ ( ι , ϕ )
ϕ = 1
ν
∑
ι = 1
ν
∑

8. TSP.8
Constraints
• Each city must be “exited” exactly once
• Each city must be “entered” exactly once
x ( i , j )
j = 1
ν
∑ = 1 , ι = 1 , 2 , ..., ν
x ( i , j )
i = 1
ν
∑ = 1 , ϕ = 1 , 2 , ..., ν

9. TSP.9
Is this enough ?

10. TSP.10
No!
• The first two constraints allow sub-
tours
• Thus, we have to add a constraint that
will prevent sub-tours

11. TSP.11
Explanation: sub-tours
• Two subtour: (1,2,1) and (3,4,3)
• This solution is not feasible for the TSP
x =
0 1 0 0
1 0 0 0
0 0 0 1
0 0 1 0











12. TSP.12
• If we start at the home city n=1, we will
not visit city 3 and 4.
• We must go from city 2 to either city 3
or city 4.
1
2
3
4

13. TSP.13
Subtour elimination constraint
• S = subset of cities
• |S| = cardinality of S (# of elements in S)
• There are 2n
such sets !!!!!!!
x ( i , j ) ≤ Σ
ι , ϕ ∈ Σ
∑ − 1 , ∀ Σ ⊂ { 1 , 2 , ..., ν }

14. TSP.14
Example
• Consider S={1,2}, |S|=2
x =
0 1 0 0
1 0 0 0
0 0 0 1
0 0 1 0










x ( i , j ) = 2
ι , ϕ ∈ Σ
∑
• Hence the sub-tour
elimination constraint is
not satisfied.
• Indeed, thee are two
subtours in this solution

15. TSP.15
Thus, LP Version
min
x
x ( i , j ) d ( i , j )
j = 1
ν
∑
ι = 1
ν
∑
σ . τ.
ξ ( ι , ϕ) = 1 , ι = 1 , 2 , ..., ν
ϕ = 1
ν
∑
ξ ( ι , ϕ) = 1 , ϕ = 1 , 2 , ..., ν
ι = 1
ν
∑
ξ ( ι , ϕ) ≤ Σ − 1 , ∀ Σ ⊂ { 1 , 2 , ..., ν }
ι , ϕ∈ Σ
ν
∑
ξ ( ι , ϕ) ∈ { 0 , 1 }

16. TSP.16
LP-Free Version
• Decision variables:
xj := j-th city on the tour, j=1,2,…,n
• Example:
• x=(1,3,2,4,1)
• We start at city 1, then go to city 3,
then go to city 2 then go to city 4 then
return to city 1.

17. TSP.17
ASSUMPTION
• Assume that 0 is the home city, and
that there are n other cities

18. TSP.18
Objective function
z = δ ( 0 , ξ
1
) + δ ( ξ
ϕ
ϕ = 1
ν − 1
∑ , ξ
ϕ + 1
) + δ ( ξ
ν
, 0 )

19. TSP.19
Constraints
• The constraint basically says that x
is a permutation of the cities (1,2,3,
…,n)
• Make sure that you appreciate the
role of { } in this formulation.
x
1
, ..., x
n
{ } = { 1 , 2 , 3 , ..., ν }

20. TSP.20
LP-Free Formulation
• There are n! feasible solutions
x
1
, ..., x
n
{ } = { 1 , 2 , 3 , ..., ν }
min
x
d ( 0 , x
1
) + δ ( ξ
ϕ
ϕ = 1
ν − 1
∑ , ξ
ϕ + 1
) + δ ( ξ
ν
, 0 )







21. TSP.21
Which one do you prefer?

22. TSP.22
LP Version
min
x
x ( i , j ) d ( i , j )
j = 1
ν
∑
ι = 1
ν
∑
σ . τ.
ξ ( ι , ϕ) = 1 , ι = 1 , 2 , ..., ν
ϕ = 1
ν
∑
ξ ( ι , ϕ) = 1 , ϕ = 1 , 2 , ..., ν
ι = 1
ν
∑
ξ ( ι , ϕ) ≤ Σ − 1 , ∀ Σ ⊂ { 1 , 2 , ..., ν }
ι , ϕ∈ Σ
ν
∑
ξ ( ι , ϕ) ∈ { 0 , 1 }

23. TSP.23
LP Free Version
x
1
, ..., x
n
{ } = { 1 , 2 , 3 , ..., ν }
min
x
d ( 0 , x
1
) + δ ( ξ
ϕ
ϕ = 1
ν − 1
∑ , ξ
ϕ + 1
) + δ ( ξ
ν
, 0 )







24. TSP.24
DP Solution
• Let,
f(i,s) := shortest sub-tour given that we
are at city i and still have to visit the
cities in s (and return to home city)
Then clearly,
f (i,φ) = d(i,0), φ = empty set
f (i,s) = min
j ∈S
d(i, j) + f (j,s {j}){ }, s ≠ φ
s A:= {k ∈ s,k ∉ A}.

25. TSP.25
Explanation
• Then clearly, …..
(i,s)
We are at city i
and still have to
visit the cities
in s
Suppose we decide
that from here we
go to city j
Then we shall travel
the Distance d(i,j)
(j,s{j})
We are now at
city j and still
have to visit the
cities in s{j}
f (i,φ) = d(i,0), φ = empty set
f (i,s) = min
j ∈S
d(i, j) + f (j,s {j}){ }, s ≠ φ
s A := {k ∈ s,k ∉ A}.

26. TSP.26
Example (Winston, p. 751)
• Distance (miles)
• Cities: New York, Miami, Dallas, Chicago
d =
− 1334 1559 809
1334 − 1343 1397
1559 1343 − 921
809 1397 921 −
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥

27. TSP.27
Initialization (s=φ)
• f(1, φ) = d(1,0) = 1334
• f(2, φ) = d(2,0) = 1559
• f(3, φ) = d(3,0) = 809

28. TSP.28
Iteration (on, i and s)
• We shall generate s systematically by its “size”.
• Size = 1: Possible values for s: {1}, {2}, {3}.
• s = {1} : f(2,{1})= ? ; f(3,{1})= ?
• s = {2} : f(1,{2})= ? ; f(3,{2})= ?
• s = {3} : f(1,{3})= ? ; f(2,{3})= ?

29. TSP.29
|s|=1
f(i,{j}) = d(i,j)+f(j, φ)
• f(2,{1})= d(2,1) + f(1,φ) = 1343 + 1334 = 2677
• f(3,{1})= d(3,1) + f(1,φ) = 1397 + 1334 = 2731
• f(1,{2})= d(1,2) + f(2,φ) = 1343 + 1559 = 2902
• f(3,{2})= d(3,2) + f(2,φ) = 921 + 1559 = 2480
• f(1,{3})= d(1,3) + f(3,φ) = 1397 + 809 = 2206
• f(2,{3})= d(2,3) + f(3,φ) = 921 + 809 = 1730

30. TSP.30
|s| = 2
f(i,s)= min{d(i,j)+f(j,s{j}): j in s}
• Size = 2: Possible values for s: {1,2}, {1,3}, {2,3}
Thus, we have to determine the values of
• f(3,{1,2}) = ? ; f(2,{1,3}) = ? ; f(1,{2,3}) = ?
• Eg:
f(3,{1,2}) = min {d(3,j) + f(j,s{j}): j in {1,2} }
= min {d(3,1) + f(1,{2}) , d(3,2) + f(2,{1})}
= min {1397+2902,921+2677}
= min {4299,3598}
= 3598 , N(3,{1,2})={2}

31. TSP.31
|s| = 3
• In this case there is only one feasible s, namely
s={1,2,3}.
• Thus, there is only one equation to solve, namely
for i=0, s={1,2,3}. The value of f(0,{1,2,3}) is the
shortest tour.
• Note that in this case
• f(0,{1,2,3})=min {d(0,j) + f(j,{1,2,3}{j}: j in {1,2,3}
• = min {d(0,1)+f(1,{2,3}), d(0,2)+ f(2,{1,3}), d(0,3)+f(3,
{1,2})}
• =min {1334+3073, 1559+3549, 809 + 3598}
• = min {4407,5108,4407} = 4407, N(0,{1,2,3})={1,3}

32. TSP.32
Recovery
• S=(0,{1,2,3}), N(s)={1,3} , c=1
• S={1,{2,3}}, N(s)={2}, c=(1,2)
• S={2,{3}}, N(s)={3}, c=(1,2,3).
• Hence: x*=(0,1,2,3,0), z*=4407