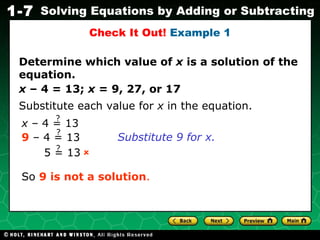
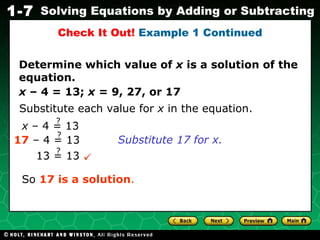
The document provides examples and explanations for solving simple linear equations and inequalities over rational numbers. It includes examples of determining if a number is a solution to an equation by substitution, using inverse operations like addition and subtraction to isolate variables, and applying equations to word problems involving forces. Step-by-step workings are shown for solving equations and checking solutions.

1. Warm Up California Standards Lesson Presentation Preview

2. Warm Up Add, subtract, multiply, or divide. 41 4 – 42 36 – 8 1. 24 + 17 2. 23 – 19 3. 12  3 4. 6(–7) 5. 6. –250 + (–85) – 335 – 64 8

3. Preparation for AF4.0 Students solve simple linear equations and inequalities over the rational numbers. AF1.4 Use algebraic terminology (e.g., variable, equation , term, coefficient, inequality, expression, constant) correctly. California Standards

4. Vocabulary equation inverse operation

5. An equation is a mathematical sentence that uses an equal sign to show that two expressions have the same value. All of these are equations. 3 + 8 = 11 r + 6 = 14 – 24 = x – 7 = 50 To solve an equation that contains a variable, find the value of the variable that makes the equation true. This value of the variable is called the solution of the equation. – 100 2

6. Determine which value of x is a solution of the equation. x + 8 = 15; x = 5, 7, or 23 Additional Example 1: Determining Whether a Number is a Solution of an Equation Substitute each value for x in the equation. Substitute 5 for x.  So 5 is not solution . 13= 15 ? x + 8 = 15 ? 5 + 8 = 15 ?

7. Determine which value of x is a solution of the equation. x + 8 = 15; x = 5, 7, or 23 Additional Example 1 Continued Substitute each value for x in the equation. Substitute 7 for x.  So 7 is a solution . 15= 15 ? x + 8 = 15 ? 7 + 8 = 15 ?

8. Determine which value of x is a solution of the equation. x + 8 = 15; x = 5, 7, or 23 Additional Example 1 Continued Substitute each value for x in the equation. Substitute 23 for x.  So 23 is not a solution . 31= 15 ? x + 8 = 15 ? 23 + 8 = 15 ?

9. Determine which value of x is a solution of the equation. x – 4 = 13; x = 9, 27, or 17 Check It Out! Example 1 Substitute each value for x in the equation. Substitute 9 for x.  So 9 is not a solution . 5 = 13 ? x – 4 = 13 ? 9 – 4 = 13 ?

10. Determine which value of x is a solution of the equation. x – 4 = 13; x = 9, 27, or 17 Check It Out! Example 1 Continued Substitute each value for x in the equation. Substitute 27 for x.  So 27 is not a solution . 23 = 13 ? x – 4 = 13 ? 27 – 4 = 13 ?

11. Determine which value of x is a solution of the equation. x – 4 = 13; x = 9, 27, or 17 Check It Out! Example 1 Continued Substitute each value for x in the equation. Substitute 17 for x.  So 17 is a solution . 13 = 13 ? x – 4 = 13 ? 17 – 4 = 13 ?

12. Adding and subtracting by the same number are inverse operations . Inverse operations “undo” each other. To solve an equation, use inverse operations to isolate the variable . In other words, get the variable alone on one side of the equal sign. The properties of equality allow you to perform inverse operations. These properties show that you can perform the same operation on both sides of an equation.

13. You can use the properties of equality along with the Identity Property of Addition to solve addition and subtraction equations .

14. Solve. Additional Example 2A: Solving Equations Using Addition and Subtraction Properties Since 10 is added to n, subtract 10 from both sides to undo the addition.  10 + n = 18 10 + n = 18 – 10 – 10 0 + n = 8 n = 8 Identity Property of Addition: 0 + n = n. Check 10 + n = 18 To check your solution, substitute 8 for n in the original equation. ? 10 + 8 = 18 18 = 18 ?

15. Solve. Additional Example 2B: Solving Equations Using Addition and Subtraction Properties Since 8 is subtracted from p, add 8 to both sides to undo the subtraction.  p – 8 = 9 p – 8 = 9 + 8 + 8 p + 0 = 17 p = 17 Identity Property of Addition: p + 0 = p. Check p – 8 = 9 To check your solution, substitute 17 for p in the original equation. ? 17 – 8 = 9 9 = 9 ?

16. Solve. Additional Example 2C: Solving Equations Using Addition and Subtraction Properties Since 11 is subtracted from y, add 11 to both sides to undo the subtraction.  22 = y – 11 22 = y – 11 + 11 + 11 33 = y + 0 33 = y Identity Property of Addition: y + 0 = y. Check 22 = y – 11 To check your solution, substitute 33 for y in the original equation. ? 22 = 33 – 11 22 = 22 ?

17. Solve. Check It Out! Example 2A Since 15 is added to n, subtract 15 from both sides to undo the addition.  15 + n = 29 15 + n = 29 – 15 – 15 0 + n = 14 n = 14 Identity Property of Addition: 0 + n = n. Check 15 + n = 29 To check your solution, substitute 14 for n in the original equation. ? 10 + 14 = 29 29 = 29 ?

18. Solve. Check It Out! Example 2B Since 6 is subtracted from p, add 6 to both sides to undo the subtraction.  p – 6 = 7 p – 6 = 7 + 6 + 6 p + 0 = 13 p = 13 Identity Property of Addition: p + 0 = p. Check p – 6 = 7 To check your solution, substitute 13 for p in the original equation. ? 13 – 6 = 7 7 = 7 ?

19. Solve. Check It Out! Example 2C Since 23 is subtracted from y, add 23 to both sides to undo the subtraction.  44 = y – 23 44 = y – 23 + 23 + 23 67 = y + 0 67 = y Identity Property of Addition: y + 0 = 0. Check 44 = y – 23 To check your solution, substitute 67 for y in the original equation. ? 44 = 67 – 23 44 = 44 ?

21. Jan and Alex are arguing over who gets to play a board game. If Jan, on the right, pulls with a force of 14 N, what force is Alex exerting on the game if the net force is 3 N? Additional Example 3: Problem Solving Application

22. Force is measured in newtons (N). The number of newtons tells the size of the force and the sign tells its direction. Positive is to the right and up, and negative is to the left and down. Helpful Hint!

23. The answer is the force that Alex, on the left, is exerting on the board game. List the important information: Jan, on the right pulls with a force of 14 N. The net force is 3 N. Show the relationship or the information: Additional Example 3 Continued Net force Alex’s force Jan’s force = + 1 Understand the Problem

24. Write an equation and solve it . Let f represent Alex’s force on the board game, and use the equation model. 3 = f + 14 3 = f + 14 Subtract 14 from both sides. – 11 = f Alex was exerting a force of – 11 N on the board game. Additional Example 3 Continued 2 Make a Plan Solve 3 – 14 – 14

25. Look Back The problem states that the net force is 3 N, which means that the person on the right, Jan, must be pulling with more force. The absolute value of Alex's force is less than the absolute value of Jan's force, |–11| < |14|, so the answer is reasonable. Additional Example 3 Continued 4

26. Frankie and Carol are playing tug of war using a rope. If Frankie, on the right, pulls with a force of 7 N, what force is Carol exerting on the game if the net force is 4 N? Check It Out! Example 3

27. The answer is the force that Carol, on the left is exerting on the rope. List the important information: Frankie, on the right pulls with a force of 7 N. The net force is 4 N. Show the relationship or the information: Check It Out! Example 3 Continued Net force Carol’s force Frankie’s force = + 1 Understand the Problem

28. Write an equation and solve it . Let f represent Carol’s force on the rope, and use the equation model. 4 = f + 7 4 = f + 7 Subtract 7 from both sides. – 3 = f Carol was exerting a force of –3 N on the rope. Check It Out! Example 3 Continued 2 Make a Plan Solve 3 – 7 – 7

29. Look Back The problem states that the net force is 4 N, which means that the person on the right, Frankie, must be pulling with more force. The absolute value of Carol's force is less than the absolute value of Frankie's force |–3| < |7|, so the answer is reasonable. Check It Out! Example 3 Continued 4

30. Lesson Quiz Determine which value of x is a solution of each equation. 1. x + 9 = 17; x = 6, 8, or 26 2. x – 3 = 18; x = 15, 18, or 21 Solve. 3. a + 4 = 22 4. n – 6 = 39 5. The price of your favorite cereal is now $4.25. In prior weeks the price was $3.69. Write and solve an equation to find n , the increase in the price of the cereal. 8 21 a = 18 n = 45 3.69 + n = 4.25; $0.56