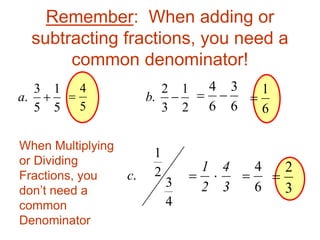
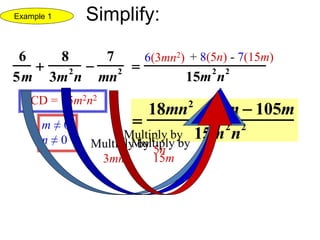
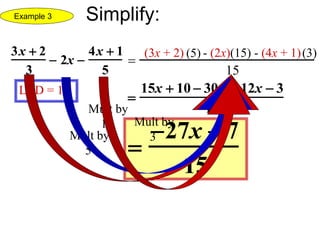
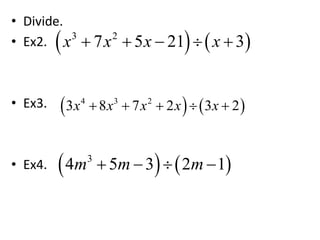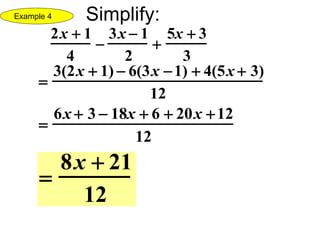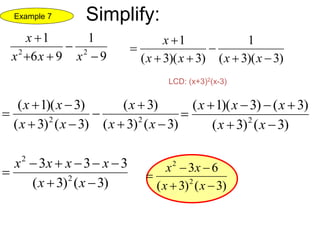1) The document discusses simplifying, multiplying, dividing, adding and subtracting rational expressions and radical functions. It provides examples and steps for simplifying, multiplying, dividing, rational expressions and finding common denominators when adding or subtracting them. 2) The document also discusses dividing polynomials using long division and provides examples. It explains how to add and subtract rational expressions with polynomial denominators by finding the least common denominator. 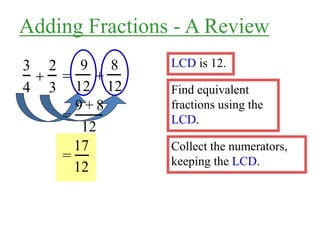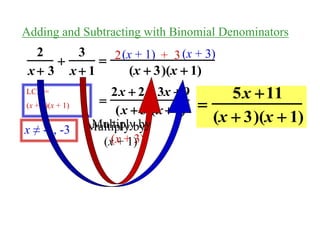3) Additional examples are given for adding and subtracting rational expressions with binomial and polynomial denominators. Steps are outlined for finding the least common denominator in order to combine like terms in the numerator.

1. CHAPTER 9
Simplifying, Multiplying, Dividing,
Adding and Subtracting
Radical Functions

2. Simplifying Rational Expressions
• Any expression that has a variable in the
denominator is a rational expression
• A rational expression is in simplest form if the
numerator and the denominator have no
common factors except 1
• To simplify rational expressions, you will often
have to factor (chapter 9)
• Ex1. Simplify 2
3 15
9 20
x
x x

 

3. • Simplify each of the following
• Ex2.
• Ex3.
2
6 12
4
x
x


2
2
20
7 12
m m
m m
 
 

4. Multiplying and Dividing Rational
Expressions
• You multiply rational expressions like you do
rational numbers
• Be sure to reduce if possible
• Multiply and simplify (if possible). Leave in
factored form.
• Ex1. Ex2.4
3 6
x x
x x


  2
4 10 15
5 12
x x
x x
 

 

5. • Divide rational expressions just like you would
rational numbers
• Leave answers in factored form
• Remember to flip the 2nd rational expression
• Divide
• Ex3. Ex4.
2
2 4 8
5 3 15
x x
x x x
 

 
 
2
2
2
7 12
5 4
3
x x
x x
x x
 
  


6. 12 – 5 Dividing Polynomials
• To divide a polynomial by a monomial, divide each
term of the polynomial by the monomial divisor
(you will often end up with rational parts to your
function)
• Ex1. Divide.
• To divide a polynomial by a binomial, you follow the
same process you use in long division
• If the dividend has terms missing (i.e. x³ + x + 1) you
must include that term (0x² in this case)
4 3 2
(6 10 8 ) 2x x x x  

7. • Divide.
• Ex2.
• Ex3.
• Ex4.
   3 2
7 5 21 3x x x x    
   4 3 2
3 8 7 2 3 2x x x x x    
   3
4 5 3 2 1m m m   

8. Adding and Subtracting
Rational Expressions
Goal 1 Determine the LCM of
polynomials
Goal 2 Add and Subtract Rational
Expressions

9. What is the Least Common Multiple?
Least Common Multiple (LCM) - smallest number
or polynomial into which each of the numbers or
polynomials will divide evenly.
Fractions require you to find the Least Common Multiple (LCM) in order to add
and subtract them!
The Least Common Denominator is the LCM
of the denominators.

10. Find the LCM of each set of
Polynomials
1) 12y2, 6x2 LCM = 12x2y2
2) 16ab3, 5a2b2, 20ac LCM = 80a2b3c
3) x2 – 2x, x2 - 4 LCM = x(x + 2)(x – 2)
4) x2 – x – 20, x2 + 6x + 8
LCM = (x + 4) (x – 5) (x + 2)

11. 3
4

2
3
LCD is 12.
Find equivalent
fractions using the
LCD.

9
12

8
12
=
9 + 8
12
=
17
12
Collect the numerators,
keeping the LCD.
Adding Fractions - A Review

12. Remember: When adding or
subtracting fractions, you need a
common denominator!
5
1
5
3
. a
5
4

2
1
3
2
. b
6
3
6
4

6
1

4
3
2
1
.c
3
4
2
1

6
4

3
2

When Multiplying
or Dividing
Fractions, you
don’t need a
common
Denominator

13. 1. Factor, if necessary.
2. Cancel common factors, if possible.
3. Look at the denominator.
4. Reduce, if possible.
5. Leave the denominators in factored form.
Steps for Adding and Subtracting Rational Expressions:
If the denominators are the same,
add or subtract the numerators and place the result
over the common denominator.
If the denominators are different,
find the LCD. Change the expressions according to
the LCD and add or subtract numerators. Place the
result over the common denominator.

14. Addition and Subtraction
Is the denominator the same??
• Example: Simplify

4
6x

15
6x

2
3x
2
2





5
2x
3
3



 Simplify...
2
3x

5
2x
Find the LCD: 6x
Now, rewrite the expression using the LCD of 6x
Add the fractions...
4 15
6x
= 19
6x

15. 6
5m

8
3m2
n

7
mn2 
15m2
n2

18mn2
 40n  105m
15m2
n2
LCD = 15m2n2
m ≠ 0
n ≠ 0
6(3mn2) + 8(5n) - 7(15m)
Multiply by
3mn2
Multiply by
5n
Multiply by
15m
Example 1 Simplify:

16. Examples:
xx
a
2
7
2
3
. 
x2
4

x
2

4
6
4
3
.


 xx
x
b
4
63



x
x
4
)2(3


x
x
or
Example 2

17. 3x  2
3
 2x 
4x  1
5

15

15x  10  30x  12x  3
15

27x  7
15
LCD = 15
(3x + 2) (5) - (2x)(15) - (4x + 1)(3)
Mult by
5
Mult by
15 Mult by
3
Example 3 Simplify:

18. 2x  1
4

3x  1
2

5x  3
3

3(2x  1)  6(3x 1)  4(5x  3)
12

6x  3  18x  6  20x 12
12

8x  21
12
Example 4 Simplify:

19. 4a
3b

2b
3a
LCD = 3ab

3ab

4a2
 2b2
3ab
a ≠ 0
b ≠ 0
Example 5
(a) (b)(4a) - (2b)
Simplify:

20. Adding and Subtracting with polynomials as denominators
Simplify:

3x  6
x  2  x  2 

8x 16
x  2  x  2 

3
(x  2)
x  2
x  2




8
(x  2)
x  2
x  2



 Simplify...
3
x  2

8
x  2
Find the LCD:
Rewrite the expression using the LCD of (x + 2)(x – 2)

3x  6  (8x 16)
(x  2)(x  2)
– 5x – 22
(x + 2)(x – 2)
(x + 2)(x – 2)

3x  6  8x 16
(x  2)(x  2)

21. 2
x  3

3
x  1

(x  3)(x  1)
LCD =
(x + 3)(x + 1)
x ≠ -1, -3

2x  2  3x  9
(x  3)(x  1) 
5x 11
(x  3)(x  1)
2 + 3(x + 1) (x + 3)
Multiply by
(x + 1)
Multiply by
(x + 3)
Adding and Subtracting with Binomial Denominators

22. 233
363
4
xx
x
x 
 ** Needs a common denominator 1st! Sometimes it
helps to factor the denominators to make it easier to
find your LCD.
)12(33
4
23


xx
x
x
LCD: 3x3(2x+1)
)12(3)12(3
)12(4
3
2
3





xx
x
xx
x
)12(3
)12(4
3
2



xx
xx
)12(3
48
3
2



xx
xx
Example 6 Simplify:

23. 9
1
96
1
22




xxx
x
)3)(3(
1
)3)(3(
1





xxxx
x
)3()3(
)3(
)3()3(
)3)(1(
22






xx
x
xx
xx
LCD: (x+3)2(x-3)
)3()3(
)3()3)(1(
2



xx
xxx
)3()3(
333
2
2



xx
xxxx
)3()3(
63
2
2



xx
xx
Example 7 Simplify:

24. 2x
x  1

3x
x  2

(x  1)(x  2)
x ≠ 1, -2 
2x2
 4x 3x2
 3x
(x 1)(x  2)

x2
 7x
(x  1)(x  2)
2x (x + 2) - 3x (x - 1)
Example 8 Simplify:

25. 3x
x2
 5x  6

2x
x2
 2x  3
(x + 3)(x + 2) (x + 3)(x - 1)
LCD
(x + 3)(x + 2)(x - 1)

(x  3)(x  2)(x  1)
3x

3x2
 3x  2x2
 4x
(x  3)(x  2)(x  1)

x2
 7x
(x  3)(x  2)(x  1)
x ≠ -3, -2, 1
- 2x(x - 1) (x + 2)
Simplify:Example 9

26. 4x
x2
 5x  6

5x
x2
 4x  4
(x - 3)(x - 2) (x - 2)(x - 2)

(x  3)(x  2)(x  2)
4x + 5x

4x2
 8x  5x2
15x
(x  3)(x  2)(x  2)

9x2
 23x
(x  3)(x  2)(x  2)
x ≠ 3, 2
(x - 2) (x - 3)
LCD
(x - 3)(x - 2)(x - 2)
Example 10 Simplify:

27. x  3
x2
1

x  4
x2
 3x  2
(x - 1)(x + 1) (x - 2)(x - 1)

(x  1)(x  1)(x  2)
(x + 3) - (x - 4)

(x2
 x  6)  (x2
 3x  4)
(x 1)(x 1)(x  2)

4x  2
(x  1)(x  1)(x  2)
x ≠ 1, -1, 2
(x - 2) (x + 1)
LCD
(x - 1)(x + 1)(x - 2)
Simplify:Example 11

28. • Add or subtract
• Ex1. Ex2.
• Ex3. Ex4.
6 7
2 2x x

 
4 1 5
3 4 3 4
x x
x x
 

 
2
1 6
9 14 7
x x
x x x


  
2 1 3
4 2
x x
x x


 