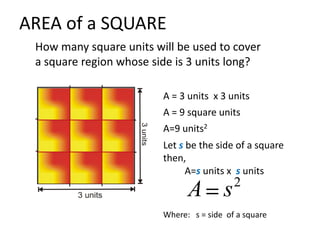
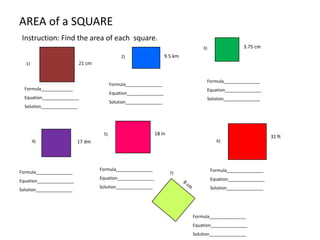
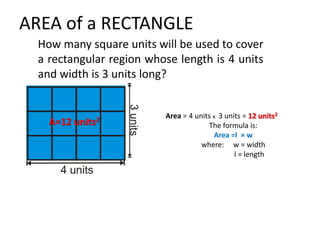
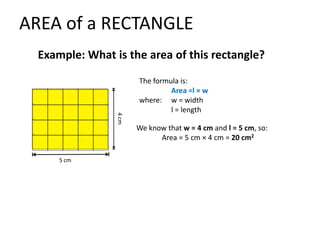
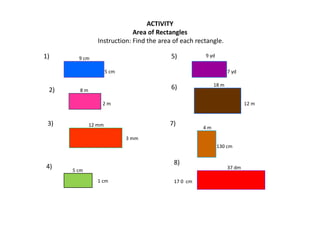
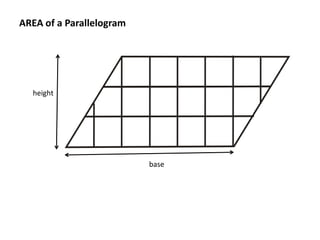
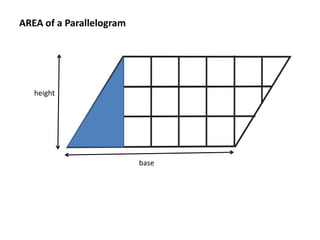
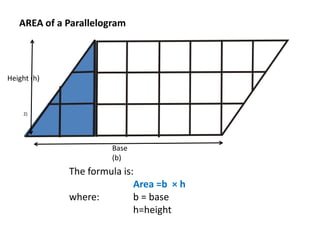
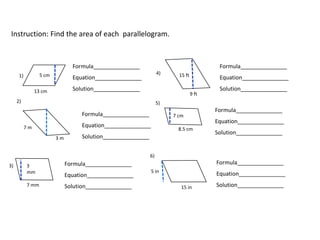
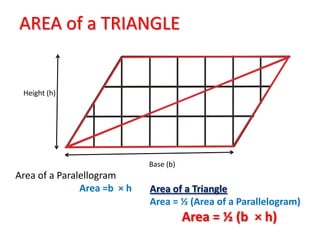
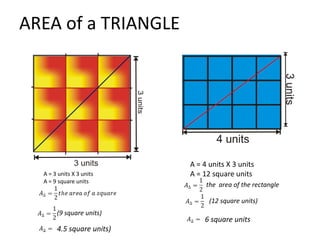
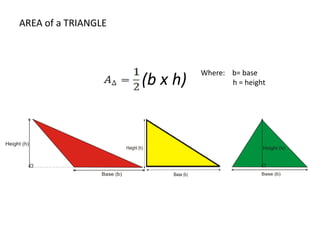
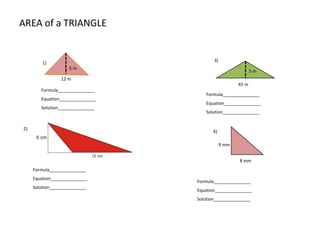
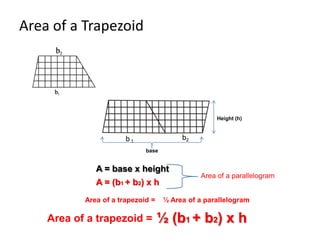
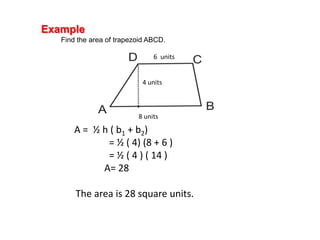
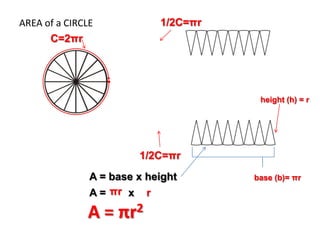
The document discusses how to calculate the area of different shapes including squares, rectangles, parallelograms, triangles, trapezoids, and circles. It provides the formulas for finding the area of each shape and works through examples of applying the formulas. Key formulas include: the area of a square is s2, the area of a rectangle is length x width, the area of a parallelogram is base x height, the area of a triangle is 1/2 x base x height, and the area of a circle is πr2.

1. AREA
Richard B. Paulino
INRSF – Laoag City

2. AREA
A square with a side of 1 unit has an area of 1 square unit in symbol
1 unit2
Hence, the unit of measure used for measuring the area of a plane
figure is square unit (unit2 )
Unit for Side Unit for AREA
cm cm2 (square centimeter)
m m2 (square meter)
ft ft2 (square feet)
– size of a surface or region.
- the number of square units to cover a surface or region.

3. AREA of a SQUARE
How many square units will be used to cover
a square region whose side is 3 units long?
2
sA
A = 3 units x 3 units
A = 9 square units
A=9 units2
Where: s = side of a square
Let s be the side of a square
then,
A=s units x s units

4. AREA of a SQUARE
21 cm
9.5 km
3.75 cm
18 in
31 ft
17 dm
1)
3)
7)
5)
4) 6)
2)
Formula_____________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Instruction: Find the area of each square.

5. AREA of a RECTANGLE
How many square units will be used to cover
a rectangular region whose length is 4 units
and width is 3 units long?
Area = 4 units x 3 units = 12 units2
The formula is:
Area =l × w
where: w = width
l = length
A=12 units2

6. AREA of a RECTANGLE
Example: What is the area of this rectangle?
5 cm
4cm
The formula is:
Area =l × w
where: w = width
l = length
We know that w = 4 cm and l = 5 cm, so:
Area = 5 cm × 4 cm = 20 cm2

7. ACTIVITY
Area of Rectangles
Instruction: Find the area of each rectangle.
9 cm
5 cm
9 yd
7 yd
8 m
2 m
12 mm
3 mm
5 cm
1 cm
18 m
12 m
4 m
130 cm
37 dm
17 0 cm
2)
5)1)
6)
3) 7)
4)
8)

8. Name:_______________________________ Score: ____
Grade/section: ____________ Date: _____
ACTIVITY
Instruction: Find the area of each rectangle using the given measures.
1 l = 7 km ,w= 14 km 6. l = 2.6 cm , w = 5 cm
2. l = 7 cm , w = 1.5 cm 7. l = 21 ft , w = 12 ft
3. l = 18 yd , w = 9 yd 8. l = 3.75 ft , w = 4.5 ft
4. l = 9.5 in , w = 9 in 9. l = 31 mm , w = 23 mm
5. l = 13 km , w = 8 km 10. l = 11 dm , w = 6 dm

9. ACTIVITY
AREA OF RECTANGLES
Instruction: Answer the following problems completely.
1. The measure of a basketball court is 26 cm by 14 cm, find its area.
Given: ____________________
Required:__________________
Formula: __________________
Equation/Number Sentence:__________________
Solution/Answer: __________________________
2. Find the area of a baseball court with the measure of 90 ft by 60 ft.
Given: ____________________
Required:__________________
Formula: __________________
Equation/Number Sentence:__________________
Solution/Answer: __________________________
3 . One face of chalk box has a length 60 cm and its width is 30 cm, find its area.
Given: ____________________
Required:__________________
Formula: __________________
Equation/Number Sentence:__________________
Solution/Answer: __________________________
4. If the measure of a volleyball court is 50ft by 70 ft, what is its area.
Given: ____________________
Required:__________________
Formula: __________________
Equation/Number Sentence:__________________
Solution/Answer: __________________________
5. The measure of a fishpond is 26 m by 78 m, find its area.
Given: ____________________
Required:__________________
Formula: __________________
Equation/Number Sentence:__________________
Solution/Answer: __________________________

10. Name:_______________________________ Score: ____
Year/section: ____________ Date: _____
ACTIVITY
Instruction: Answer the following problems completely.
6. Find the floor area of the gymnasium whose length and width is 65 m and 45 m
respectively.
7. A badminton court has a measure of 27 m by 36 m, find its area.
8. Find the width of a rectangle with the area of 186 square yards and a length of
13 yards.
9. One dimension of rectangular pool table is 76 cm. Its area is 8664 cm2, find the
other dimension.
10. The length of the base of the table in the canteen is 15 m and the length of the
diagonal is 17 m. Find its area.

11. AREA of a Parallelogram
height
base

12. AREA of a Parallelogram
height
base

13. AREA of a Parallelogram
2)
Height (h)
Base
(b)
The formula is:
Area =b × h
where: b = base
h=height

14. 1)
2)
6)
3)
5)
4)5 cm
13 cm
15 ft
9 ft
7 m
3 m
7 cm
8.5 cm
15 in
5 in
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Instruction: Find the area of each parallelogram.

15. AREA of a TRIANGLE
Height (h)
Base (b)
Area of a Paralellogram
Area =b × h Area of a Triangle
Area = ½ (Area of a Parallelogram)
Area = ½ (b × h)

16. AREA of a TRIANGLE
A = 3 units X 3 units
A = 9 square units
A = 4 units X 3 units
A = 12 square units
(9 square units)
4.5 square units)
the area of the rectangle
(12 square units)
6 square units

17. AREA of a TRIANGLE
(b x h)
Where: b= base
h = height

18. Example

19. AREA of a TRIANGLE
5 m
5 m
45 m
2)
1)
3)
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
12 m
9 mm
8 mm
4)
Formula_______________
Equation_______________
Solution_______________

20. Area of a Trapezoid
b1
b2
A = base x height
Height (h)
Area of a parallelogram
base
A = (b1 + b2) x h
Area of a trapezoid = ½ Area of a parallelogram
Area of a trapezoid = ½ (b1 + b2) x h

21. Example
Find the area of trapezoid ABCD.
6 units
4 units
8 units
A = ½ h ( b1 + b2)
= ½ ( 4) (8 + 6 )
= ½ ( 4 ) ( 14 )
A= 28
The area is 28 square units.

22. 3 m
7.25 m
2.5 m
18 cm
25 cm
6 cm
10 ft
5 ft
4 ft
3 m
2 m
7 m
5 ft
3 ft
10 ft
5 in
14 in
23 in
Formula_______________
Equation_______________
Solution_______________ Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
Formula_______________
Equation_______________
Solution_______________
2)
5)
1)
6)
3)
4)
Instruction: Find the area of each trapezoid.

23. AREA of a CIRCLE
Radius (r)
C=2πr
1/2C=πr
1/2C=πr
base (b)= πr
height (h) = r
A = base x height
A =
A = πr2
x rπr

24. d = 6 cm
Example 1
The radius of a circle is 2 cm. Find its area.
Solution:
A = r2 r=2 cm
3.14 (2)2 ●
12.56 cm2
The area is 12.56 square cm.
Example 2
The diameter of a circle is 6 cm. Find its area.
Solution:
Step 1. Find the radius
Radius( r ) = diameter (d) divided by 2
r = 6 2
r = 3 cm
The radius is 3 cm. ●
Step 2. Find the area.
A = r2
3.14 (3)2
3.14 (9)
28.26 cm2
The area is 28.26 cm2

25. Try this out
Find the area of each circle with the given diameter or
radius Use 3.14 for .
1. `radius = 5 cm
2. radius = 1.5 mm
3. diameter = 4 cm
4. diameter = 12 dm
5. radius = 4.6 m
6. radius = 2.2 cm
7. diameter = 4.8 dm
8. diameter = 6.4 cm
9. radius = 4.8 m
10. radius = 3.4 dm

26. Let’s Summarize
1. The area of a region is the number of square units
contained in the region.
2. A square unit is a square with a side 1 unit in length.
The area (A) of a rectangle is the product of its length
(l) and its width (w). A = lw
3. The area (A) of a square is the square of the length
of a side (s). A = s2
4. The area (A) of a parallelogram is equal to the
product of the base (b) and the height (h). A = bh

27. 5. The area (A) of a triangle equals half the product of
the base (b) and the height (h). A = ½ bh. Sometimes
altitude is used instead of height.
6. The area (A) of a trapezoid is one half the product of
the length of its altitude and the sum of the lengths of
the two bases. A = ½ h (b1 + b1).
7. A circle is a set of points in a plane that have the
same distance from a given point in the plane.
8.The formula for the area of a circle with a radius of r
and diameter of d units are: A = r2 and A = (d/2)2
respectively.
Note: In all circles the ratio of the circumference to the diameter is always equal to the
same number, represented by the Greek letter .