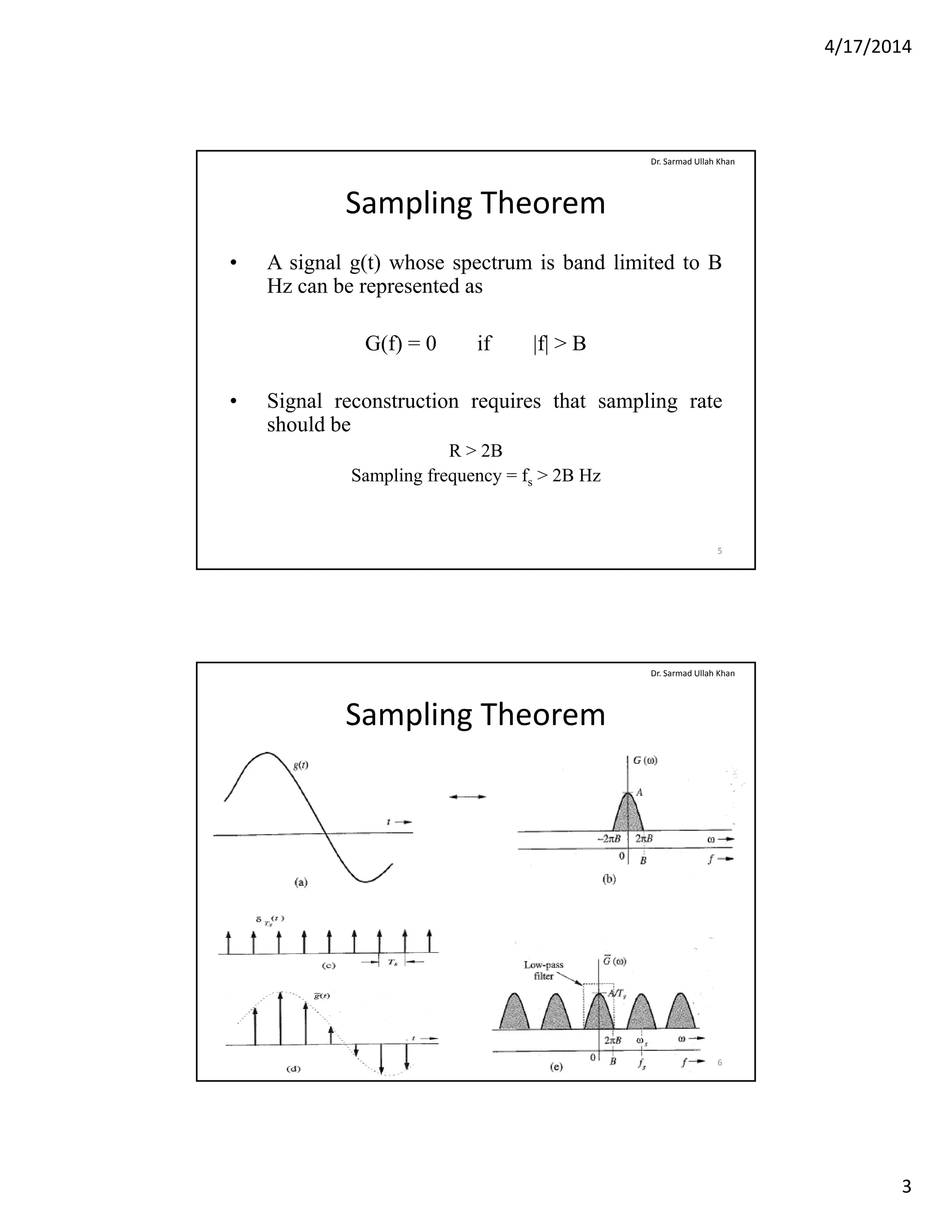
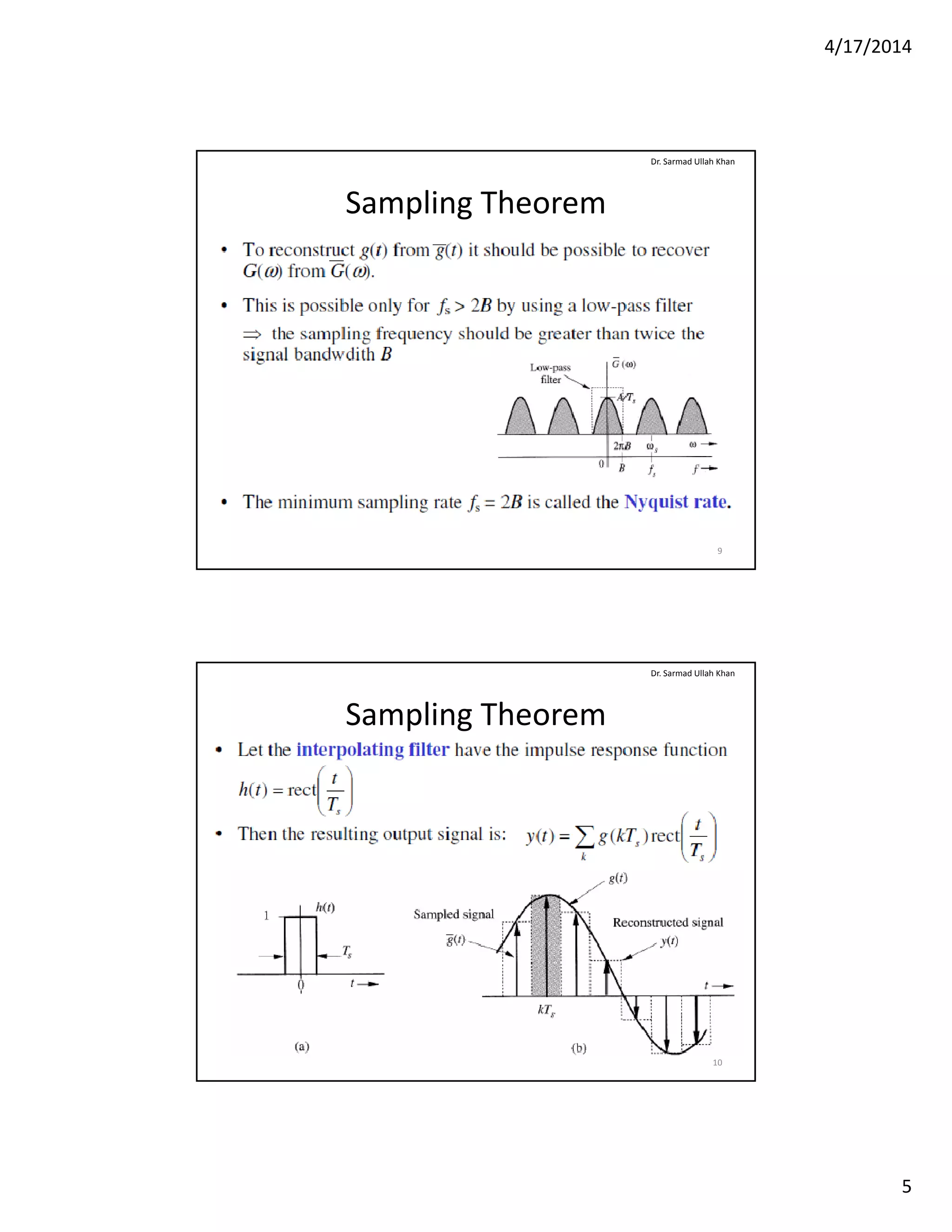
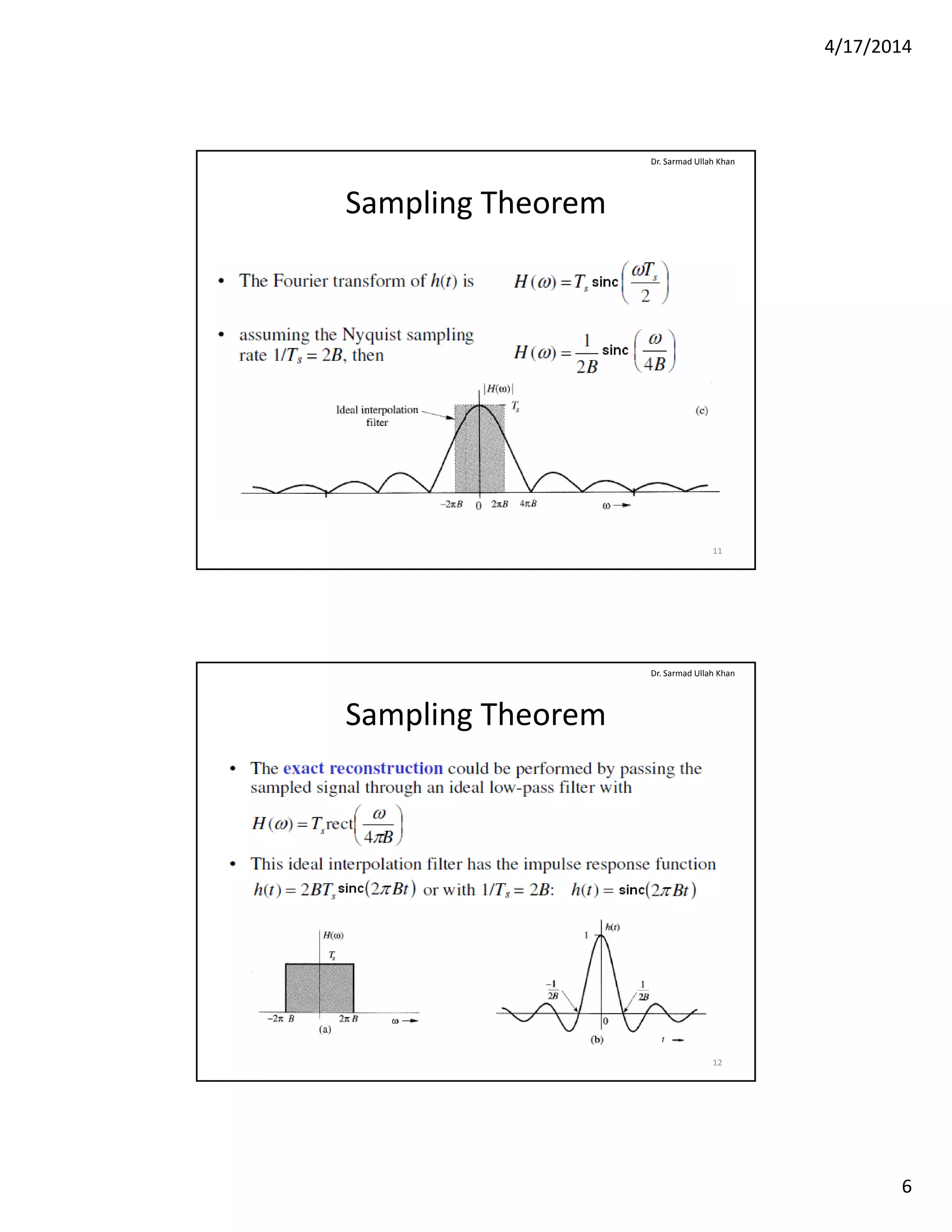
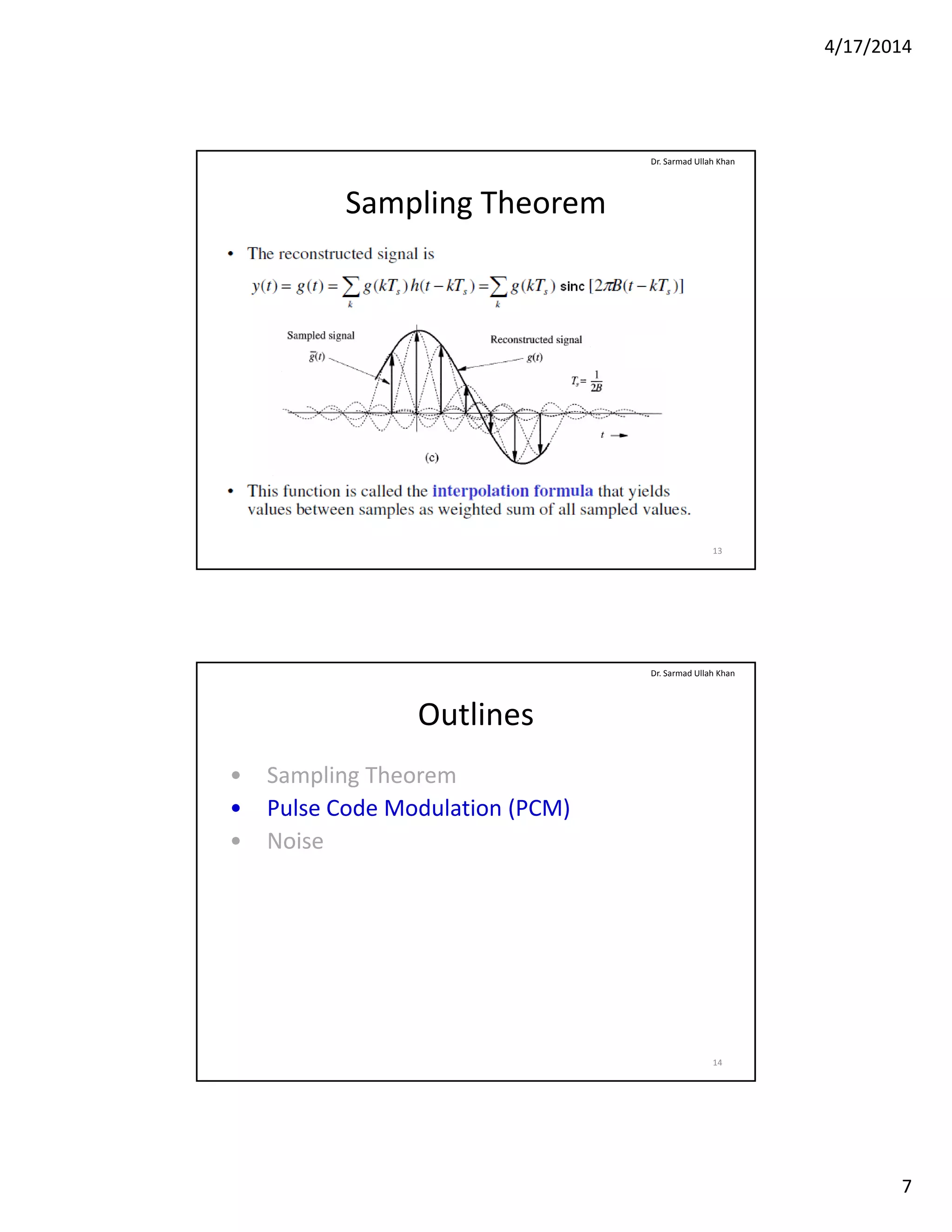
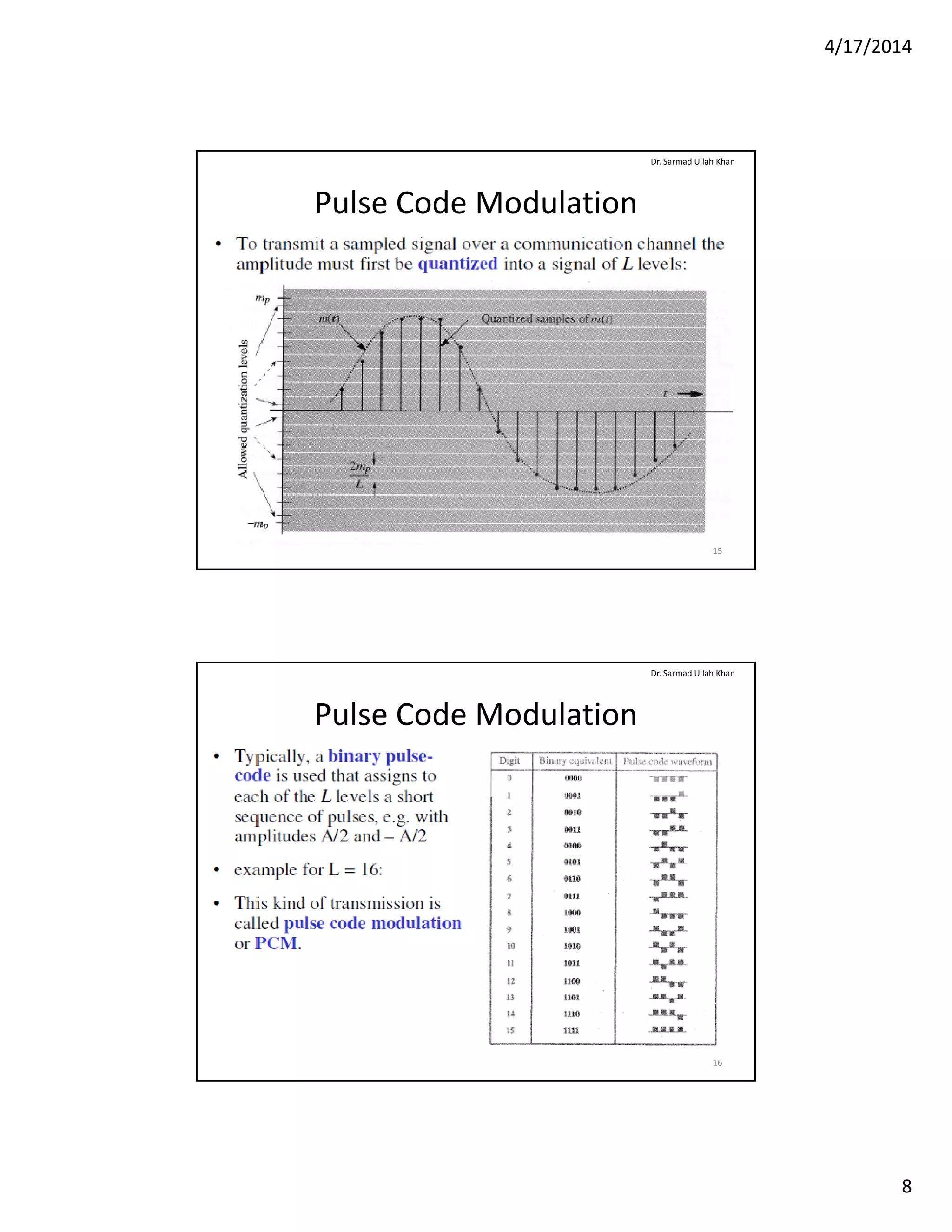
The document outlines key concepts of sampling and analog to digital conversion, focusing on the sampling theorem, pulse code modulation (PCM), and noise. It emphasizes that a signal's sampling rate must exceed twice its bandwidth for accurate reconstruction and discusses various types of noise impacting communication systems. Additionally, it details the characteristics and measurements of noise, including signal-to-noise ratio and noise factor, relevant to amplifiers in communication systems.