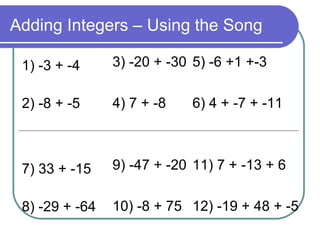
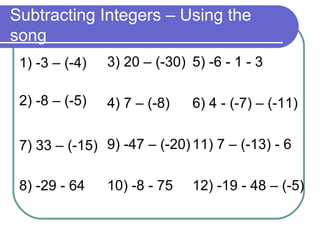
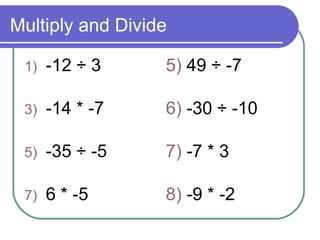
This document provides an overview of operations with integers including: - Defining integers as positive and negative whole numbers including 0 - Ordering and comparing integers - Absolute value and opposite of integers - Adding and subtracting integers using number lines and sign rules - Multiplying and dividing integers and the sign of the result - Properties like distributive property for operations with integers

1. Chapter 2 Integers + - * ÷

2. Integers Integers- Negative and Positive whole numbers. INCLUDES 0 Write some integers on your paper: …-4, -3, -2, -1, 0, 1, 2, 3, 4…

3. Ordering integers Order the following from least to greatest: -7, 2, -1, 0, -2 -7, -2, -1, 0, 2 9, -4, 12, -11, -1 -11, -4, -1, 9, 12 3) 0, -99, 44, -60, 16 -99, -60, 0, 16, 44

4. Absolute Value Absolute Value- The distance between the number and zero on a number line. The absolute value of n looks like: │ n │ Find the absolute value of the following: │ 6 │ │ -8 │ │ 15 │

5. Opposite Opposite of a number- same distance from 0. On different sides of 0. Opposite numbers have the same AV. Find the opposite: -6 14 -27

6. Evaluate: - │ 8 │ - │ -5 │ (-6) -(- 4)

7. Do Now 9/30 Write the opposite and Absolute Value: 18 -45 -16 Evaluate: 4) -(-2) 5) - │ -18 │

8. Adding Integers – Number Line Use your number line to add integers: Positive numbers right, Negative numbers left 3 + (-4) -5 + 2 Start at zero Move 3 units to the right Move 4 units to the left 1) Start at zero 2) Move 5 units to the left 3) Move 2 units to the right

9. Adding Integers – Number Line Use your number line to add integers: Positive numbers right, Negative numbers left 3) -6 + -1 4) -4 + 2 1) Start at zero 2) Move 6 units to the left 3) Move 1 unit to the left 1) Start at zero 2) Move 4 units left 3) Move 2 units right

10. Do Now 10/1/09 Add using a number line: 7 + (-10) -2 + ( -3) -8 + 5 5 + 3

11. Adding Integers- Walking on a number line -2 + 4 7 + (-8) -6 + -3 5 + (-4) -8 + 3 -2 + (-7) 12 + (-8) -16 + 9 9) 9 + (-11) 10) -6 + 14 11) 17 + (-7) 12) -14 + - 6 13) 7 + (-4) 14) -8 + 8 15) -12 + (-7) 16) 15 + (-8) 17) 19 + (-11) 18) -16 + 3 19) 7 + (-7) 20) -16 + - 2 21) 15 + (-8) 22) -8 + 3 23) -12 + (-2) 24) 19 + (-7)

12. What are the Adding Integer RULES?! Write a rule for: (+) + (+) (-) + (- ) ( - ) + (+) / (+) + (- )

13. Adding Integers - Integer song: Integer Operations Song ( Row Row Row Your Boat) Same sign - add and keep Different sign - subtract Keep the sign of the bigger number Then you’ll be exact.

14. Adding Integers – Using the Song 1) -3 + -4 2) -8 + -5 7) 33 + -15 8) -29 + -64 3) -20 + -30 4) 7 + -8 9) -47 + -20 10) -8 + 75 5) -6 +1 +-3 6) 4 + -7 + -11 11) 7 + -13 + 6 12) -19 + 48 + -5

15. Do Now 10/5 Add: -35 + 42 -64 + -37 3) 73 + -19 4) -128 + -84

16. Adding Integers – Zero Pairs zero pairs- is a pair of numbers whose sum is zero. 4 + -7 3 + -2 -6 + 5 -3 + - 4

17. Subtracting Integers – Add Opposite Subtract Integers- Add the opposite of the second number. 11 – 12 -5 – 3 -7 – (-6) 8 – (-2)

18. Do Now 10/7/09 Subtract – Add the opposites -6 – 9 72 – 114 -18 – (-88) 25 – (-93)

19. Subtracting Integers –Song Subtract – no, don’t do! Just change the second sign Now add the numbers like you did And then you will be fine

20. Subtracting Integers – Using the song 1) -3 – (-4) 2) -8 – (-5) 7) 33 – (-15) 8) -29 - 64 3) 20 – (-30) 4) 7 – (-8) 9) -47 – (-20) 10) -8 - 75 5) -6 - 1 - 3 6) 4 - (-7) – (-11) 11) 7 – (-13) - 6 12) -19 - 48 – (-5)

21. Do Now- 10/8/09 Subtract: -8 – (-3) - 74 – 19 -56 – (-32) 43 – 93

22. Adding and Subtracting Integers Be careful, you have to decide which rule to follow (adding or subtracting) -54 + 84 - 35 – 32 49 – 9 23 + -84 -34 - 63 6) - 5 – 28 7) 19 – 57 8) 38 + -45 9) -79 + -11 10) -42 – 34

23. Do Now 10/14/09 Add or subtract: 14 + -12 48 – 59 -71 + - 34 -84 - 49

24. Multiplying and Dividing Integers- Multiply and Divide numbers as you normally do. -If both signs are positive or negative the answer is positive -If one sign is positive and one sign is negative the answer is negative

25. Multiply and Divide -12 ÷ 3 -14 * -7 -35 ÷ -5 6 * -5 5) 49 ÷ -7 6) -30 ÷ -10 7) -7 * 3 8) -9 * -2

26. Do Now 10/15 1) 20 * (-3) 2) 16 ÷ (-8) 3) -40 ÷ (-20) 4) -8 * 5

27. Multiplying and Dividing with Zeros Zero – 0 Multiplying- 0 * -32 = 0 Dividing- 0 ÷ -4 = 0 = -4 -4 ÷ 0= -4 = 0 0 undefined = u

28. Multiplying and Dividing Integers- Song Multiply or Divide - what do I do now? Same sign- positive – Different sign- negative I got it now KERPOW!!

29. Multiplying and Dividing Integers- Song -10 ÷ 5 -2 * -7 * 5 -90 ÷ -5 6 * -3 * -3 5) 49 ÷ -7 6) -110÷ -10 7) -7 * -4 * -2 8) -9 * -12

30. Do Now 10/16 Add/subtract/Multiply and Divide 5 + -3 -3 * 7 -28 ÷ -2 14 – (-8)

31. Peer Grading of projects Tell what Grade you should get and why on back of rubric. Show each other all the rules on your project. (check that each person included all parts of the rules) Show each other all the real life examples on your project. (check that there are atleast 3 and that they are different ideas).

32. Do Now: Identify the following properties of Math (use your text if you forgot): 1- Identity Property- Sum of a number and zero = the number Product of a number and 1 = the number a + 0 = a b * 1 = b 2- Commutative Property- Can add or multiply numbers in any order a+b = b +a cd= dc 3-Associative Property- Changing the grouping will not affect the sum or product a + (b+c) = (a + b) + c abc= cba

33. Distributive Property- You can multiply a number and a sum by multiplying the number by each part of the sum and then adding these products. The same applies to subtraction. A(B + C) = AB + AC D(E – F) = DE – DF

34. Ex1: -5 (x + 10) -5 x + -5 (10) = -5x + -50 or = -5x – 50

35. Ex2: 2 (x - 7) 2 x - 2 (7) = 2x - 14

36. Ex3: 3 [x – 20 + (-5)] 3 (x) – 3 (20) + 3 (-5) 3x – 60 + (-15) 3x + (-60) + (-15) 3x + (-75)

37. Simplify using Distributive Property 1) -2 (5 + 12) 2) -4(-7 – 10) 3) 2(w – 8) 4) -8(z + 25)

38. Tell Which property each displays: Do Now 10/28 1) 3(2x + 1)= 6x +3 2) (2 + 4) + y = 2 + (4 + y) 4x = x*4 6(2*15)= (6*2)15

39. Like Terms- Identical variable parts raised to the same power For example: 2m and 14m 3x 4 and 12x 4 12xy 2 z and xy 2 z 3 and 62 Write 3 more examples on your page:

40. Simplify the expression by combining like terms: c + 8c 3m + -4m 15y 2 + 9y + 11y 2 -5x -7t +2x -9t

41. Like Terms- 5x – 2x 2a + 3a 7p – 3p + 25 10k + 21+ -8k 13z + 7 - 5z

42. Simplify the expressions: 9w (w + -4) 8(1 +4d) – 3d 9p – ( 7p + 2) 11(2g - 4) +12 -18g

43. Solve Equations Involving Distribution 3(x – 9) = -39 z + 4(6 – z) = 21 8 = -7(y + 1) + 2y