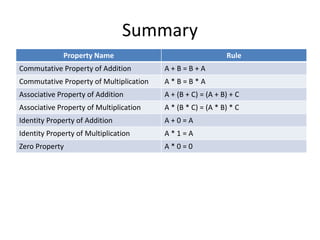
The document explains key mathematical properties including commutative, associative, identity, zero, and distributive properties. It provides definitions, examples, and the rules associated with each property, illustrating how they apply to addition and multiplication. It emphasizes that these properties hold true for all real numbers but may not apply beyond that set.

1. Math Properties
Commutative, Associative,
Distributive, Identity, and Zero
Properties
𝐴 ∗ 𝐵 = 𝐵 ∗ 𝐴

2. What are properties?
Math Properties are rules in math.
Properties are always true for every
number.
**Once you go beyond the set of Real numbers the properties may no longer hold.

3. Commute
• To commute means to travel from one place
to another.
• For example, you commute to school in the
morning.

4. Commutative Property
• Just like you commute from home to school, a
number may commute from one spot to
another.
• A + B = B + A (The numbers change places.)
• This is called the commutative property of
addition.
• Ex) 2 + 3 = 3 + 2
• Both 2 + 3 and 3 + 2 equal 5.

5. The commutative property may be used with
addition as seen previously and also with
multiplication.
• A * B = B * A
• Ex) 3 * 5 = 5 * 3
• Both 3 * 5 and 5 * 3 equal 15.
• This is called the commutative property of
multiplication.

6. Associate
• An associate is a friend or someone
you work with.
• For example, the head cheerleader is
an associate of the school mascot.

7. Now imagine the football team played a late game
and the cheerleader and mascot forgot to study for
the math test.
Suddenly the cheerleader associates
with someone else.

8. Associative Property
The associative property is when a number
associates with a different number.
A + (B + C)
(A + B) + C
A + + C
B

9. Associative Property
• (A + B) + C = A + (B + C) is called the
associative property of addition.
• Ex) (2 + 3) + 4 = 2 + (3 + 4)
• The order in which you add does not change
your answer.
• A * (B * C) = (A * B) * C is called the
associative property of multiplication.

10. Identity
• Your identity is who you are.
• Changing your clothes or getting a new haircut
does not change your identity.
• Your identity remains the same.

11. Identity Property of Addition
• A number also has an identity
• The identity of a number is the value of the
number
• The additive identity is the number that when
added to another number does not change
the identity of the original number
• 3 + __ = 3 (What goes in the blank?)
0

12. Zero
• The additive identity is zero.
• We can add zero to any number
and the answer is the original
number.

13. Identity Property of Multiplication
• We also have a multiplicative identity
• 3 * __ = 3 (What goes in this blank?)
• We can multiply any number by one and the
answer will be the original number.
1

14. Identity Properties
Identity Property of Addition
A + 0 = A
Identity Property of Multiplication
A * 1 = A

15. Zero Property
• The zero property sounds just like what it is, a
property about zero.
• A * 0 = 0
• The zero property tells us that any number
multiplied by zero equals zero.

16. Summary
Property Name Rule
Commutative Property of Addition A + B = B + A
Commutative Property of Multiplication A * B = B * A
Associative Property of Addition A + (B + C) = (A + B) + C
Associative Property of Multiplication A * (B * C) = (A * B) * C
Identity Property of Addition A + 0 = A
Identity Property of Multiplication A * 1 = A
Zero Property A * 0 = 0

17. Distribute
• Distribute means to deliver or pass out
• If we distribute food to three boxes, we put
food in each of the three boxes

18. Distributive Property
• A(B + C) = A*B + A*C
• The A is the food and the boxes are B and C.
• We pass out A to each of B and C.
• In this case that means that we multiply A by
both B and C separately and then add the
resulting products.

19. Ex) 4(X + 3)
4
X 3
4X 12
=4X + 12

20. Now you try these examples.
1) 5(X + 3) =
2) 7(X + 4) =
3) 2(Z -3) =
5X + 15
7X + 28
2Z - 6

21. Summary
Property Name Rule
Commutative Property of Addition A + B = B + A
Commutative Property of Multiplication A * B = B * A
Associative Property of Addition A + (B + C) = (A + B) + C
Associative Property of Multiplication A * (B * C) = (A * B) * C
Identity Property of Addition A + 0 = A
Identity Property of Multiplication A * 1 = A
Zero Property A * 0 = 0
Distributive Property A(B + C) = A*B + A*C