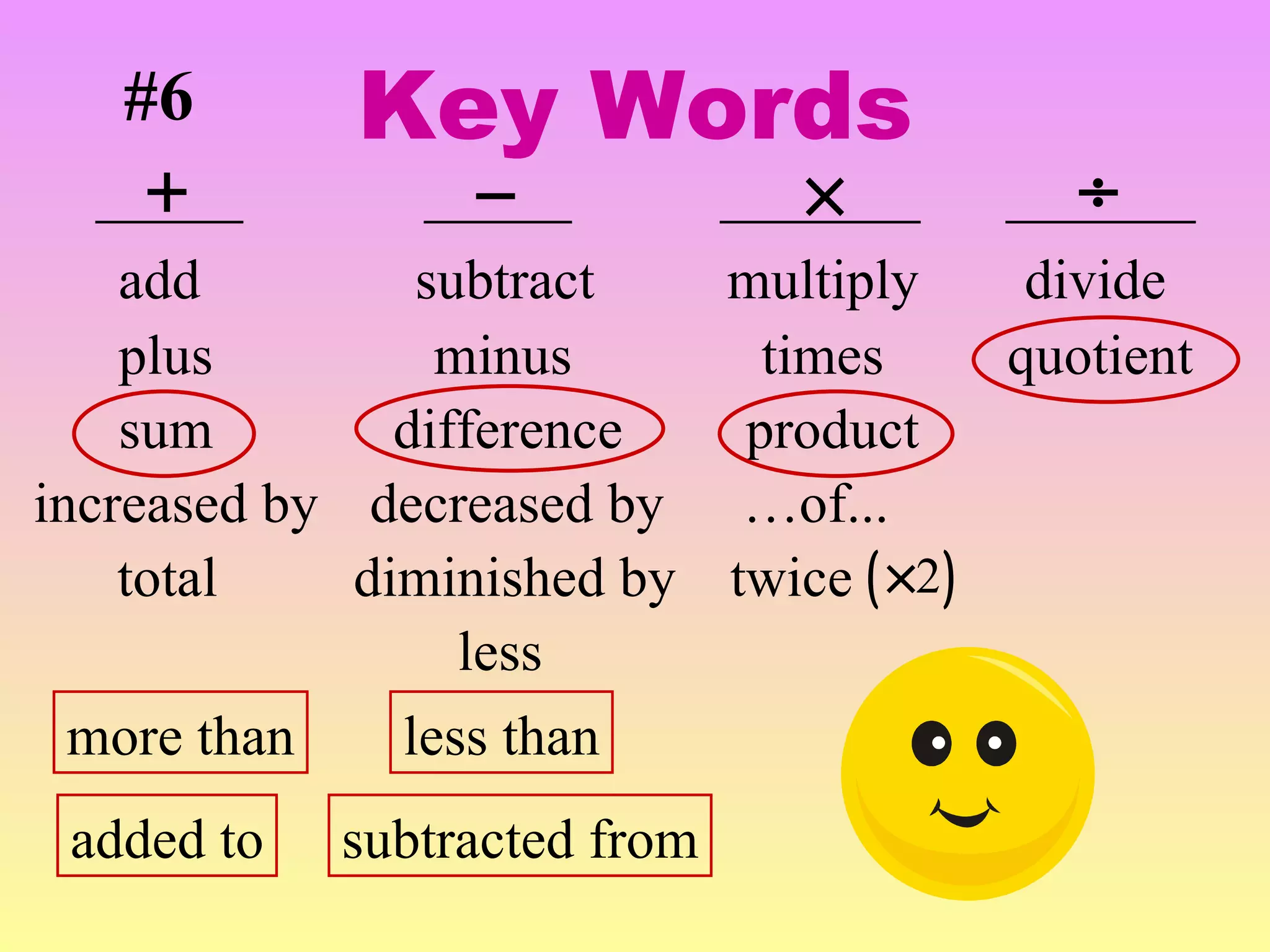
The document discusses the order of operations (PEMDAS) and provides examples of how to evaluate expressions and solve equations. It explains that parentheses, exponents, multiplication/division from left to right, and addition/subtraction from left to right have priority in calculations. Algebraic expressions and equations are introduced along with rules for manipulating integers and solving different types of equations.

1. Order Of Operations PEMDAS: P lease E xcuse M y D ear A unt S ally #1 Step 4: Add or Subtract in order by reading the problem from left to right. Step 1: Parenthesis first Step 2: Exponents or powers second Step 3: Multiply or Divide in order by reading the problem from left to right. _ _ _ _ _ _

2. The rules for order of operations exist so that everyone can perform the same consistent operations and achieve the same results. Order Of Operations Example Follow all the rules for order of operations. Remember PEMDAS #2

3. #3 Parenthesis 1 st Exponents 2 nd Mult. / Div. left to right Add / Subt. left to right P E MD AS PEMDAS

4. An expression is NOT an equation because it does not have an equal sign. There are 2 types of expressions. NUMERICAL EXPRESSION : Contains only numbers and symbols. Example: 5 3 + 4 ALGEBRAIC EXPRESSION : Contains numbers, symbols, and variables. Also known as a variable expression. Example: m + 8 A VARIABLE is a letter or symbol that represents a number. Example: x TYPES OF E X P R E S S I O N S #4

5. #5 Substitute & Evaluate when x = 2 and y = 4 Evaluate Show the substitution Show your work down Circle your answer Show your work down, one step at a time, no equal signs!

6. add plus sum increased by total more than added to subtract minus difference decreased by diminished by less than subtracted from less multiply times product … of... divide quotient Key Words #6 twice

7. WORD PHRASES A word phrase is a sentence that can be translated into a variable expression or equation. A word phrase is like a verbal phrase. It is made up of only words. Example: The difference of 8 and a number. Algebraic Expression: 8 - n #7

8. Write an Algebraic Expression for the Word Phrases. 5.8 more than 4 times a 5.8 + 4a or 4a + 5.8 The difference of 3a and 2 3a - 2 6 less than the number 58t 58t - 6 Writing Algebraic Expressions # 8

9. Integers Integers - are the set of numbers including positive whole numbers, negative whole numbers and zero. Negative Numbers Positive Numbers * Negative integers are less than zero *Positive integers are greater than zero * The integer zero is neither positive or negative #9 0 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6

10. Opposites Pairs of integers that are the same distance from zero on a number line are opposites . Example: 3 and -3 are opposites because each integer is 3 units away from zero Other Examples: 2 and –2 5 and -5 #10

11. Absolute Value Absolute value of an integer is the distance the number is from zero on a number line. Examples: |-2| = 2 |1| = 1 The absolute value of -5 is 5 spaces from zero . #11 Two vertical bars around the number means find the absolute value . 0 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6

12. Steps To Add Integers 1) Put in the 1 st number of + or – 2) Add the 2 nd number of + or – 3) Balance out what you have 5) The leftovers are the final answer Virtual Manipulative: Color Chips - Addition #12 4) One + balances out one – When a + and – cancel each other out it is called a NEUTRAL FIELD or ZERO BANK

13. Integer Addition Rules If the signs are the same Add the numbers. The sign stays the same. 4 + 3 = -4 + -3 = + + + + + + + 7 _ _ _ _ _ _ _ -7 If the signs are different Subtract the numbers. The “larger number” determines the sign of the answer. -9 + 5 = 9 - 5 = 4 Subtract the numbers - 4 #13 _ _ _ _ _ + + + + + _ _ _ _ Answer -4 because you started with more negatives

14. 8 7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 -6 -7 -8 Integer Elevator Ground Floor -5 + 2 = -3 -5 + 2 Positive = Up Negative = Down Add Integers With a Number Line #14

15. A Model to Subtract Integers 1) Put in the 1 st number of + or – 2) Subtract , or remove, the 2 nd number of + or – Show that you remove them by circling them & attaching an arrow to them. 3) IF YOU CANNOT REMOVE THE 2 nd NUMBER ADD ENOUGH ZERO PAIRS SO YOU CAN. 4) Count your remaining tiles. (one + balances out one - ) 5) Record your answer (the leftovers) #15

16. Subtract Integers Example 1 3 - 2 1) Put in 3 2) Take away 2 3) You are left with 1 = 1 3 - -2 1) Put in 3 2) You can’t take away –2 so add 2 zeros 3) Take away -2 4) You are left with + 5 = 5 + + + + + - - + + + #16

17. Subtract Integers Example 2 -3 - -2 1) Put in -3 2) Take away -2 3) You are left with -1 = -1 -3 - 2 1) Put in -3 2) You can’t take away 2 so add 2 zeros 3) Take away +2 4) You are left with -5 = -5 http://www.matti.usu.edu/nlvm/nav/frames_asid_162_g_2_t_1.html _ _ _ _ _ + + _ _ _ #17

18.  Subtracting Integer Rules Keep the first number and add the opposite . 5 – 6 5 – 6 Is the same as = -1 4 – ( – 2 ) Is the same as 4 – ( – 2 ) = 6 -3 – 1 Is the same as -3 – ( 1 ) = -4 #18 * SUBTRACT = PLUS CHANGE!

19. 8 7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 -6 -7 -8 Integer Elevator Ground Floor -4 - 2 = -6 -4 - 2 1)Start at 0. Move to the 1 st number. 2) Then look at the 2 nd number. 3) Subtract a Positive = Down 4) Subtract a Negative=Up Subtract Integers With a Number Line #19

20. To Remember Multiply & Divide Integers #20 When good things, happen to good people, that’s good! + • + = + When bad things, happen to bad people, that’s good! – • – = + When good things, happen to bad people, that’s bad! + • – = – When bad things, happen to good people, that’s bad! – • + = – +  + = + –  – = + +  – = – –  + = –

21. RULES FOR DIVIDING INTEGERS When determining the sign, the rules of multiplying integers are the same for dividing integers. If the signs are the same , the answer is positive . - 64  - 8 = 8 If the signs are different , the answer is negative . - 8  4 = -2 #21

22. 0 8 = 8 0 = 0 undefined 22 Dividing with Zero A calculator might display “ ERROR ” when you divide by 0. No ZERO in the denominator!

23. Equations An equation is a mathematical statement that shows 2 quantities are equal . An equation contains an equal sign. #23 12 – 3 = 9 Numerical 3a = 30 Algebraic To solve any equation use inverse operations . Your goal is to get the variable all by itself.

24. To solve an addition equation m + 8 = 12 Get the variable alone. – 8 –8 Subtract 8 from both sides. m = 4 +8 and -8 cancel each other out. 4 + 8 = 12 Show your check. Subtract the same number from both sides #24 12 = 12 Finish your check!

25. To solve a subtraction equation a – 15 = 22 Get the variable alone. +15 +15 Add 15 to both sides . a = 37 +15 and -15 cancel out 37 - 15 = 22 Show your check! Add the same number to both sides #25 22 = 22 Finish your check!

26. To Solve a Multiplication Equation 5x = 40 Get the variable alone. 5 5 Divide 5 into both sides. x = 8 5 divided by 5 cancels out to 1. 5 8 = 40 Show your check! Divide the same number into both sides #26 40 = 40 Finish your check!

27. To Solve a Division Equation = 20 Get the variable alone. 2 = 2 20 Multiply both sides by 2. x = 40 2 divided by 2 cancels out to 1. Show your check! x 2 x 2 Multiply the same number to both sides #27 20 = 20 Finish your check!