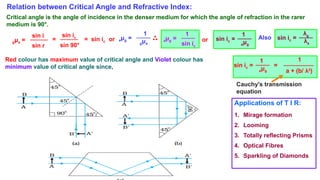
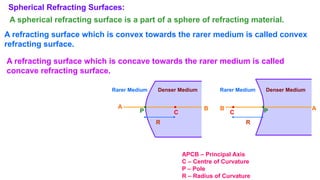
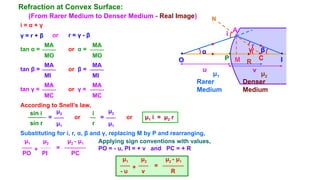
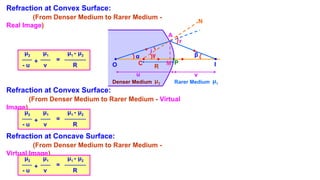
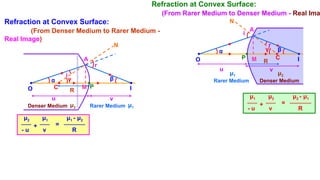
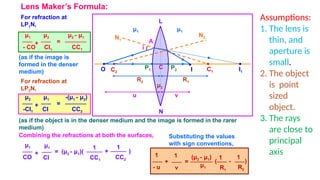
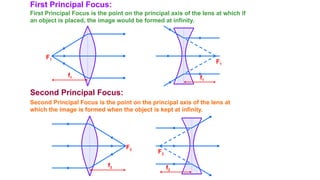
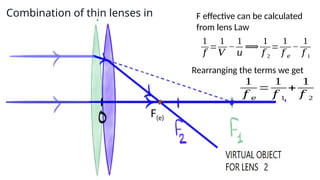
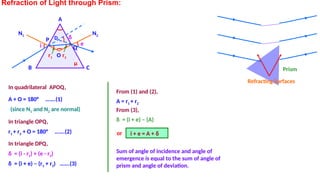
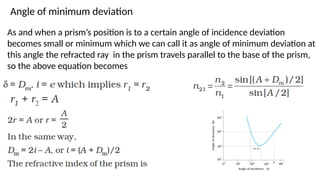
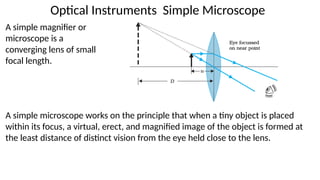
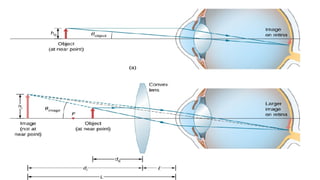
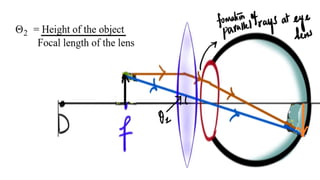
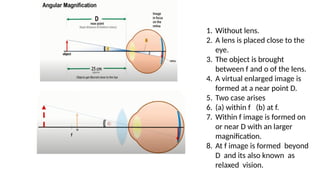
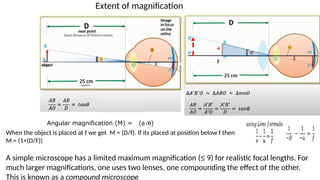
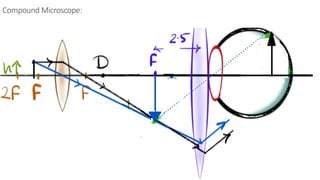
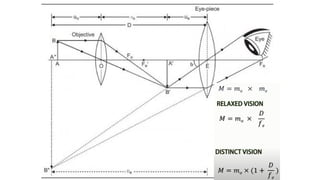
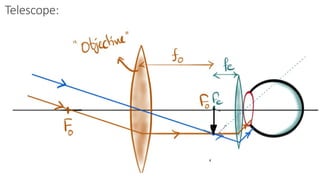
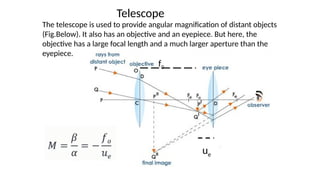
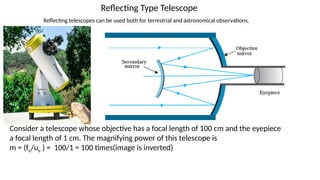
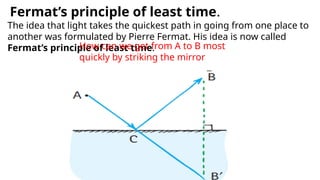
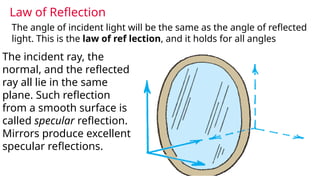
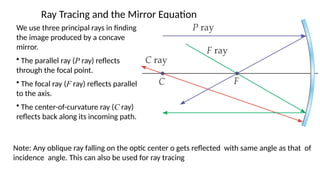
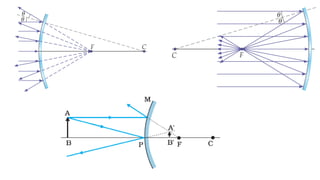
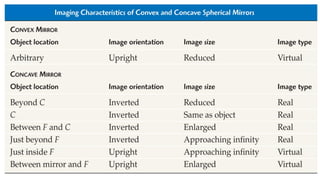
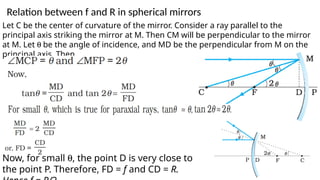
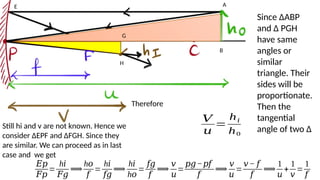
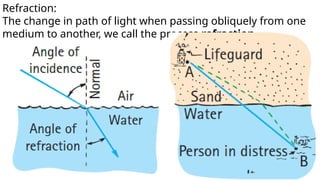
The document discusses principles of ray optics, focusing on reflection and refraction of light. It explains concepts like the law of reflection, the formation of images by mirrors, the principles of Fermat and Snell, and phenomena such as total internal reflection and apparent depth. Various equations, sign conventions, and examples illustrate the behavior of light in different media and mirror configurations.

1. RAY OPTICS

2. Reflection:
• Most of the things we see around us do not emit light of
their own. They are visible because they reemit light that
reaches their surface from a primary source, such as the
Sun or a lamp.
• When light falls on the surface of a material, it is either
reemitted without change in frequency or absorbed into
the material and converted to heat.
Note:
When sunlight or lamplight illuminates this page, electrons
in the atoms of the paper and ink vibrate more energetically
in response to the oscillating electric fields of the
illuminating light. The energized electrons reemit the light

3. Fermat’s principle of least time.
The idea that light takes the quickest path in going from one place to
another was formulated by Pierre Fermat. His idea is now called
Fermat’s principle of least time.
How can we get from A to B most
quickly by striking the mirror

4. Law of Reflection
The angle of incident light will be the same as the angle of reflected
light. This is the law of ref lection, and it holds for all angles
The incident ray, the
normal, and the reflected
ray all lie in the same
plane. Such reflection
from a smooth surface is
called specular reflection.
Mirrors produce excellent
specular reflections.

5. A light wave can be considered to travel from one point to another,
along a straight line joining them. The path is called a ray of light,
and a bundle of such rays constitutes a beam of light.
Ray and Beam:
Reflection from a smooth surface is called
specular reflection; if the surface is rough, it is
diffuse reflection.

6. Images formed by curved mirror:
• When the mirror is curved, the sizes and distances of object and
image are no longer equal.
• A curved mirror behaves as a succession of flat mirrors, each at a
slightly different angular orientation from the one next to it.
• geometric center of a
spherical mirror is called its
pole.
• The line joining the pole and
the center of curvature of the
spherical mirror is known as the
principal axis.

7. Ray Tracing and the Mirror Equation
We use three principal rays in finding
the image produced by a concave
mirror.
• The parallel ray (P ray) reflects
through the focal point.
• The focal ray (F ray) reflects parallel
to the axis.
• The center-of-curvature ray (C ray)
reflects back along its incoming path.
Note: Any oblique ray falling on the optic center o gets reflected with same angle as that of
incidence angle. This can also be used for ray tracing

10. A spherical mirror has the shape of a section of a sphere. If the outside is
mirrored, it is convex; if the inside is mirrored, it is concave.
For a convex mirror, the focal length is negative,
as the rays do not go through the focal point.
The opposite is true for a concave mirror.

11. Relation between f and R in spherical mirrors
Let C be the center of curvature of the mirror. Consider a ray parallel to the
principal axis striking the mirror at M. Then CM will be perpendicular to the mirror
at M. Let q be the angle of incidence, and MD be the perpendicular from M on the
principal axis. Then,
Now, for small q, the point D is very close to
the point P. Therefore, FD = f and CD = R.

12. MIRROR EQUATION

13. A
B
E
G
H
Since ∆ABP
and ∆ PGH
have same
angles or
similar
triangle. Their
sides will be
proportionate.
Then the
tangential
angle of two ∆
Therefore
𝑉
𝑢
=
h𝑖
h0
Still hi and v are not known. Hence we
consider ∆EPF and ∆FGH. Since they
are similar. We can proceed as in last
case and we get
𝐸𝑝
𝐹𝑝
=
h𝑖
𝐹𝑔
⟹
h𝑜
𝑓
=
h𝑖
𝑓𝑔
⟹
h𝑖
h𝑜
=
𝑓𝑔
𝑓
⟹
𝑣
𝑢
=
𝑝𝑔−𝑝𝑓
𝑓
⟹
𝑣
𝑢
=
𝑣− 𝑓
𝑓
⟹
1
𝑢
+
1
𝑣
=
1
𝑓

14. Sign convention:
A sign convention defines the position off the object or image playlist against
the mirror or lens generally any object placed on the reflective side off the
mirror is considered as negative and the back side of the mirror direction is
considered as positive .Henceforth the above equation can be rewritten with
their positions and final conclusion can be arrived
1
− 𝑓
=
1
−𝑢
+
1
−𝑣
Removing all the negative signs from the equation we get
1
𝑓
=
1
𝑢
+
1
𝑣
Similarly, the same can be applied for magnification
equation end the result would be
−
h𝐼
h0
=
− 𝑉
−𝑢
⇒
− h𝐼
h0
=
𝑣
𝑢
⇒
h𝐼
h0
=−
𝑣
𝑢

15. Suppose that the lower half of the concave mirror’s reflecting surface in Fig.
below is covered with an opaque (non-reflective) material. What effect will this
have on the image of an object placed in front of the mirror?
As the area of the reflecting surface has been reduced, the intensity of
the image will be low (in this case, half).
An object is placed at (i) 10 cm, (ii) 5 cm in front of a concave mirror of
radius of curvature 15 cm. Find the position, nature, and magnification
of the image in each case.
(i) f = -7.5, V = -30cm, magnification =-3 (ii) V = 15 and m = 3
Suppose while sitting in a parked car, you notice a jogger approaching
towards you in the side view mirror of R = 2 m. If the jogger is running
at a speed of 5 m s–1
, how fast the image of the jogger appear to move
when the jogger is (a) 39 m, (b) 29 m, (c) 19 m, and (d) 9 m away.
Ans: 3.46×10 3
−
m/s, 6.38×10 3
−
m/s, 0.0154m/s
0.078m/s

16. Refraction:
The change in path of light when passing obliquely from one
medium to another, we call the process refraction.

17. Effect on frequency speed and wavelength due to refraction of light
When a ray of light gets refracted from rarer to a denser medium the speed of light decreases
while if it is refracted from a denser to rarer medium the speed of light increases
The frequency of light depends on the source of light show it doesn't change on refraction
The speed of light in a medium is related to its wavelength and the frequency as 𝑣=𝜈𝜆
In general, the refractive index of second medium
with respect to first medium is related to the speed of
light in the 2 media as follows
1µ2 =
Henceforth the relation between wavelength in 2
mediums can be written as
𝑐
𝜆
=
𝑣
𝜆
1
𝜇=
𝑐
𝑣
=
𝜆
𝜆1
𝜆
1
=
𝜆
𝜇

18. Refraction of Light:
Refraction is the phenomenon of change in the path of
light as it travels from one medium to another (when the
ray of light is incident obliquely).
It can also be defined as the phenomenon of change in
speed of light from one medium to another.
Rarer
Rarer
Denser
N
N
r
i
r
i
Laws of Refraction:
I Law: The incident ray, the normal to the refracting surface at the point
of incidence and the refracted ray all lie in the same plane.
II Law: For a given pair of media and for light of a given wavelength, the
ratio of the sine of the angle of incidence to the sine of the angle of
refraction is a constant. (Snell’s Law)
μ = sin i
sin r
(The constant μ is called refractive index of the medium,
i is the angle of incidence and r is the angle of
refraction.)
μ

19. Note:
1. μ of optically rarer medium is lower and that of a denser medium is higher.
2. μ of denser medium w.r.t. rarer medium is more than 1 and that of rarer medium w.r.t. denser medium is
less than 1. (μair = μvacuum = 1)
3. In refraction, the velocity and wavelength of light change.
4. In refraction, the frequency and phase of light do not change.
5. aμm =Ca / V m and aμm = λa / λm
Principle of Reversibility of Light:
Rarer
(a)
N
r
i
Denser
(b)
sin i
aμb =
sin r
sin r
bμa =
sin i
aμb x bμa = 1 or aμb = 1 / bμa
If a ray of light, after suffering any number of reflections and/or
refractions has its path reversed at any stage, it travels back to
the source along the same path in the opposite direction.
A natural consequence of the principle of reversibility is that the image and object
positions can be interchanged. These positions are called conjugate positions.
μ
Refraction occurs when the
average speed of light
changes in going from one
transparent
medium to another.

20. Refraction through a Parallel Slab:
Rarer (a)
Rarer (a)
Denser
(b)
N
N
r1
i1
i2
r2
M
t
δ
y
sin i1
aμb =
sin r1
sin i2
bμa =
sin r2
But aμb x bμa = 1
sin i1
sin r1
sin i2
sin r2
x = 1
It implies that i1 = r2 and i2 = r1 since i1 ≠ r1 and i2 ≠ r2.
Lateral Shift:
t sin δ
y =
cos r1
t sin(i1- r1)
y =
cos r1
or
Special Case:
If i1 is very small, then r1 is also very small. i.e. sin(i1 – r1) = i1 – r1 and cos r1 = 1
y = t (i1 – r1) or y = t i1(1 – 1 /aμb)
μ

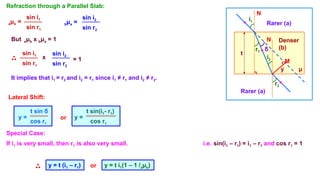
21. Apparent Depth of a Liquid:
Rarer (a)
Denser (b)
O
O’
N
μb
hr
ha
i
r
r
i
sin i
bμa =
sin r
sin r
aμb =
sin i
or
hr
aμb =
ha
=
Real depth
Apparent depth
.Apparent Depth of a Number of Immiscible Liquids:
ha = ∑ hi / μi
i = 1
n
Apparent Shift or Normal shift: Height through which an object appears to be raised in a denser
medium
Apparent shift = hr - ha = hr – (hr / μ)
= hr [ 1 - 1/μ]
μa
An object placed in a denser medium when seen from rarer
medium appears to be at the depth smaller than its actual
depth in the denser medium this is known as the apparent
depth
As the refractive index of any medium (except vacuum) is greater than Unity So
the apparent depth is lesser than real depth.
Normal Shift depends on the refractive index of the denser
medium the higher the value of μ greater the apparent
shift

22. Note:
1. If the observer is in rarer medium and the object is in denser medium then ha < hr. (To a bird, the fish
appears to be nearer than actual depth.)
2. If the observer is in denser medium and the object is in rarer medium then ha > hr. (To a fish, the bird
appears to be farther than actual height.)
An air bubble in a glass slab with refractive index 1.5 (near normal incidence) is 5 cm deep when
viewed from one surface and 3 cm deep when viewed from the opposite face. The thickness (in
cm) of the slab is
(a) 8 (b) 10 (c) 12 (d) 16.

23. Total Internal Reflection:
Total Internal Reflection (TIR) is the phenomenon of complete reflection of light back into the same medium
for angles of incidence greater than the critical angle of that medium.
N N N N
O
r = 90°
ic i > ic
i
Rarer
(air)
Denser
(glass)
μg
μa
Conditions for TIR:
1. The incident ray must be in optically denser medium.
2. The angle of incidence in the denser medium must be greater than the critical angle for the pair of media
in contact.

24. Relation between Critical Angle and Refractive Index:
Critical angle is the angle of incidence in the denser medium for which the angle of refraction in the rarer
medium is 90°.
sin i
gμa =
sin r
sin ic
=
sin 90°
= sin ic or
1
aμg =
gμa
1
aμg =
sin ic
or
1
sin ic =
aμg
Red colour has maximum value of critical angle and Violet colour has
minimum value of critical angle since,
1
sin ic =
aμg
=
1
a + (b/ λ2
)
Applications of T I R:
1. Mirage formation
2. Looming
3. Totally reflecting Prisms
4. Optical Fibres
5. Sparkling of Diamonds
λg
sin ic =
λa
Also
Cauchy's transmission
equation

25. Figure given below shows a cross-section of a ‘light pipe’ made of a glass fibre of
refractive index 1.68. The outer covering of the pipe is made of a material of
refractive index 1.44. What is the range of the angles of the incident rays with the
axis of the pipe for which total reflections inside the pipe take place, as shown in
the figure.
A small coin is resting on the bottom of a beaker filled with liquid. A ray of light
from the coin travels upto the surface of the liquid and moves along its surface.
How fast is the light travelling in the liquid?
(a) 2.4 × 108
m/s (b) 3.0 × 108
m/s (c) 1.2 × 108
m/s (d) 1.8 × 108
m/s.

26. An object is placed at a distance of 40 cm from a concave mirror of focal
length 15 cm. If the object is displaced through a distance of 20 cm towards
the mirror, the displacement of the image will be
(a) 30 cm away from the mirror (b) 36 cm away from the mirror (c) 30 cm towards
the mirror
(d) 36 cm towards the mirror
The direction of ray of light incident on a concave mirror is shown by PQ
while directions in which the ray would travel after reflection is shown by
four rays marked 1, 2, 3 and 4 (Fig. given alongside). Which of the four rays
correctly shows the direction of reflected ray?
(a) 1 (b) 2 (c) 3 (d) 4
A concave mirror of focal length 15 cm forms are image
having twice the linear dimensions of the object. The
position of the object, when the image is virtual, will be
(a) 22.5 cm (b) 7.5 cm (c) 30 cm (d) 45 cm
A short pulse of white light is incident from air to a glass slab at normal
incidence. After
travelling through the slab, the first colour to emerge is

27. Spherical Refracting Surfaces:
A spherical refracting surface is a part of a sphere of refracting material.
A refracting surface which is convex towards the rarer medium is called convex
refracting surface.
A refracting surface which is concave towards the rarer medium is called
concave refracting surface.
•
•
C C
P P
R R
A B A
B
APCB – Principal Axis
C – Centre of Curvature
P – Pole
R – Radius of Curvature
•
•
Denser Medium
Denser Medium Rarer Medium
Rarer Medium

28. Assumptions:
1. Object is the point object lying on the principal axis.
2. The incident and the refracted rays make small angles with the principal axis.
3. The aperture (diameter of the curved surface) is small.
(The diameter (length) of the reflecting surface of the spherical mirror is called the aperture.)
New Cartesian Sign Conventions:
1. The incident ray is taken from left to right.
2. All the distances are measured from the pole of the refracting surface.
3. The distances measured along the direction of the incident ray are taken
positive and against the incident ray are taken negative.
4. The vertical distances measured from principal axis in the upward
direction are taken positive and in the downward direction are taken
negative.

29. Refraction at Convex Surface:
(From Rarer Medium to Denser Medium - Real Image)
•
C
P
R
O
•
Denser
Medium
Rarer
Medium
• •
I
M
μ2
μ1
α β
γ
i
r
i = α + γ
γ = r + β or r = γ - β
A
tan α =
MA
MO
tan β =
MA
MI
tan γ =
MA
MC
or α =
MA
MO
or β =
MA
MI
or γ =
MA
MC
According to Snell’s law,
μ2
sin i
sin r μ1
= or
i
r μ1
=
μ2
or μ1 i = μ2 r
Substituting for i, r, α, β and γ, replacing M by P and rearranging,
μ1
PO
μ2
PI
μ2 - μ1
PC
+ =
Applying sign conventions with values,
PO = - u, PI = + v and PC = + R
v
u
μ1
- u
μ2
v
μ2 - μ1
R
+ =
N

30. Refraction at Convex Surface:
(From Denser Medium to Rarer Medium -
Real Image)
•
C P
R
O
•
Denser Medium Rarer Medium
• •
I
M
μ2 μ1
α β
γ
r
A
v
u
N
i
μ2
- u
μ1
v
μ1 - μ2
R
+ =
Refraction at Convex Surface:
(From Denser Medium to Rarer Medium - Virtual
Image)
μ2
- u
μ1
v
μ1 - μ2
R
+ =
Refraction at Concave Surface:
(From Denser Medium to Rarer Medium -
Virtual Image)
μ2
- u
μ1
v
μ1 - μ2
R
+ =

31. Note:
1. Expression for ‘object in rarer medium’ is same for whether it is real or virtual
image or convex or concave surface.
2. Expression for ‘object in denser medium’ is same for whether it is real or
virtual image or convex or concave surface.
3. However the values of u, v, R, etc. must be taken with proper sign
conventions while solving the numerical problems.
4. The refractive indices μ1 and μ2 get interchanged in the expressions.
μ1
- u
μ2
v
μ2 - μ1
R
+ =
μ2
- u
μ1
v
μ1 - μ2
R
+ =

32. Refraction at Convex Surface:
(From Rarer Medium to Denser Medium - Real Ima
•
C
P
R
O
•
Denser Medium
Rarer Medium
• •
I
M
μ2
μ1
α β
γ
i
r
A
v
u
μ1
- u
μ2
v
μ2 - μ1
R
+ =
N
Refraction at Convex Surface:
(From Denser Medium to Rarer Medium -
Real Image)
•
C P
R
O
•
Denser Medium Rarer Medium
• •
I
M
μ2 μ1
α β
γ
r
A
v
u
N
i
μ2
- u
μ1
v
μ1 - μ2
R
+ =

33. An air bubble is trapped at point B (CB = 20cm) in a glass sphere of radius 40 cm
and refractive index 1.5 as shown in figure. Find the nature and position of the
image of the bubble as seen by an observer at point P.

34. Lens Maker’s Formula:
R1
P1
•
O
•
μ2
μ1
i
A
v
u
N1
R2
C1
• •
I1
N2
L
C
N
P2
•
C2
•
I
•
μ1
For refraction at
LP1N,
μ1
- CO
μ2
CI1
μ2 - μ1
CC1
+ =
(as if the image is
formed in the denser
medium)
For refraction at
LP2N,
(as if the object is in the denser medium and the image is formed in the rarer
medium)
μ2
-CI1
μ1
CI
-(μ1 - μ2)
CC2
+ =
Combining the refractions at both the surfaces,
μ1
CO
(μ2 - μ1)(
CC1
+ =
1
μ1
CI CC2
+ )
1
Substituting the values
with sign conventions,
1
- u
(μ2 - μ1)
R1
+ =
1
1
v R2
- )
1
(
μ1
Assumptions:
1. The lens is
thin, and
aperture is
small.
2. The object
is point
sized
object.
3. The rays
are close to
principal
axis

35. Since μ2 / μ1 = μ
1
- u
μ2
R1
+ =
1
1
v R2
- )
1
(
μ1
- 1)
(
or
1
- u
(μ – 1)
R1
+ =
1
1
v R2
- )
1
(
When the object is kept at infinity, the image is formed at the principal focus.
i.e. u = - ∞, v = + f.
So, (μ – 1)
R1
=
1
1
f R2
- )
1
(
This equation is called ‘Lens Maker’s Formula’.
Also, from the above equations we get,
1
- u f
+ =
1
1
v

36. First Principal Focus:
First Principal Focus is the point on the principal axis of the lens at which if
an object is placed, the image would be formed at infinity.
F1
f1
F2
f2
Second Principal Focus:
Second Principal Focus is the point on the principal axis of the lens at
which the image is formed when the object is kept at infinity.
F2
f2
F1
f1

37. Thin Lens Formula (Gaussian Form of Lens Equation):
For Convex Lens:
f
•
R
u
C
A
B
A’
B’
M
Triangles ABC and A’B’C are similar.
A’B’
AB
=
CB’
CB
Triangles MCF2 and A’B’F2 are similar.
A’B’
MC
=
B’F2
CF2
v
A’B’
AB
=
B’F2
CF2
or
•
2F2
•
F2
•
F1
•
2F1
CB’
CB
=
B’F2
CF2
CB’
CB
=
CB’ - CF2
CF2
According to new Cartesian sign
conventions,
CB = - u, CB’ = + v and CF2 = + f.
1
v f
- =
1
1
u

38. Linear Magnification:
Linear magnification produced by a lens is defined as the ratio of the size of the image to the size of the
object.
m =
I
O
A’B’
AB
=
CB’
CB
+ I
- O
=
+ v
- u
According to new Cartesian sign
conventions,
A’B’ = + I, AB = - O, CB’ = + v and
CB = - u.
m
I
O
=
v
u
=
or
Magnification in terms of v and f:
m =
f - v
f
Magnification in terms of u and f:
m =
f
f - u
Power of a Lens:
Power of a lens is its ability to bend a ray of light falling on it and is reciprocal of its focal length. When f is in
metre, power is measured in Dioptre (D).
P =
1
f

39. Combination of thin lenses in
contact
F(e)
F effective can be calculated
from lens Law
1
𝑓
=
1
𝑉
−
1
𝑢
⟹
1
𝑓 2
=
1
𝑓 𝑒
−
1
𝑓 1
Rearranging the terms we get
1
𝑓 𝑒
=
1
𝑓 1
+
1
𝑓 2

40. Significance of combining lenses:
1. The derivation is valid for any number of thin lenses in contact. If several thin
lenses of focal length f1, f2, f3,... are in contact, the effective focal length of their
combination is given by
2. In terms of power, Eq. can be written as
4. Since the image formed by the first lens becomes the object for the second, Eq
implies that the total magnification m of the combination is a product of
magnification (m1, m2, m3,...) of individual lenses m = m1 m2 m3 ...
where P is the net power of the lens combination. Note that the sum in Eq. is an
algebraic sum of individual powers, so some of the terms on the right side may
be positive (for convex lenses) and some negative (for concave lenses)
3. Combination of lenses helps to obtain diverging or converging lenses of desired
magnification. It also enhances sharpness of the image.

43. Refraction of Light through Prism:
A
Refracting Surfaces
Prism
i
δ
A
B C
e
O
P
Q
r1 r2
N1 N2
D
In quadrilateral APOQ,
A + O = 180° …….(1)
(since N1 and N2 are normal)
In triangle OPQ,
r1 + r2 + O = 180° …….(2)
In triangle DPQ,
δ = (i - r1) + (e - r2)
δ = (i + e) – (r1 + r2) …….(3)
From (1) and (2),
A = r1 + r2
From (3),
δ = (i + e) – (A)
or i + e = A + δ
μ
Sum of angle of incidence and angle of
emergence is equal to the sum of angle of
prism and angle of deviation.

44. Angle of minimum deviation
As and when a prism’s position is to a certain angle of incidence deviation
becomes small or minimum which we can call it as angle of minimum deviation at
this angle the refracted ray in the prism travels parallel to the base of the prism,
so the above equation becomes

45. Strontium titanate is a rare oxide a natural mineral found in Siberia. It is used as a substitute for diamond because its refractive
index and critical angle are 2.41 and 24.5°, respectively, which are approximately equal to the refractive index and critical angle
of diamond. It has all the properties of diamond. Even an expert jeweller is unable to differentiate between diamond and
strontium titanate. A ray of light is incident normally on one face of an equilateral triangular prism ABC made of
strontium titanate. ( board exam 2023)
(a) Trace the path of the ray showing its passage through the prism.1
(b) (b) Find the velocity of light through the prism.1
(c) Briefly explain two applications of total internal reflection. 2
OR
(c) Define total internal reflection of light. Give two conditions for it. (2)
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it
just suffers total internal reflection at the other face? The refractive index of prism is 1.524.

46. Optical Instruments Simple Microscope
A simple magnifier or
microscope is a
converging lens of small
focal length.
A simple microscope works on the principle that when a tiny object is placed
within its focus, a virtual, erect, and magnified image of the object is formed at
the least distance of distinct vision from the eye held close to the lens.

49. 1. Without lens.
2. A lens is placed close to the
eye.
3. The object is brought
between f and o of the lens.
4. A virtual enlarged image is
formed at a near point D.
5. Two case arises
6. (a) within f (b) at f.
7. Within f image is formed on
or near D with an larger
magnification.
8. At f image is formed beyond
D and its also known as
relaxed vision.

50. Extent of magnification
Angular magnification (M) = (f /q)
When the object is placed at f we get M = (D/f). If its placed at position below f then
M = (1+(D/F))
A simple microscope has a limited maximum magnification (£ 9) for realistic focal lengths. For
much larger magnifications, one uses two lenses, one compounding the effect of the other.
This is known as a compound microscope

51. Compound Microscope:

53. 1. A compound microscope has an objective of focal length 1 cm and an eyepiece
of focal length 2.5 cm. An object has to be placed at a distance of 1.2 cm away
from the objective for normal adjustment. (a) Find the angular magnification. (b)
Find the length of the microscope tube.
2. The radii of curvature of the faces of a double-convex lens are 20 cm and 30 cm. Its power
is(25/6) D. What is the refractive index of the glass of the lens?
3. solid glass sphere of radius 6-0 cm has a small air bubble trapped at a distance 3.0 cm from
its centre C as shown in the figure. The refractive index of the material of the sphere is 1.5.
Find the apparent position of this bubble when seen through the surface of the sphere from an
outside point E in air
4. The power of a thin lens is +5 D. When it is immersed in a
liquid, it behaves like a concave lens of focal length 100 cm.
Calculate the refractive index of the liquid. Given refractive
index of glass = 1.5.

54. Telescope:

55. Telescope
The telescope is used to provide angular magnification of distant objects
(Fig.Below). It also has an objective and an eyepiece. But here, the
objective has a large focal length and a much larger aperture than the
eyepiece.
f0
ue

56. Working principle:
•A telescope bring the far object near and then it magnifies.
• The objective has a large focal length and a much larger aperture
than the eyepiece.
•Light from a distant object enters the objective and a real image is
formed in the tube at its second focal point.
•The eyepiece magnifies this image producing a final inverted image.
•The magnifying power m is the ratio of the angle b subtended at
the eye by the final image to the angle a which the object subtends
at the lens or the eye.
•Hence
The above formula holds good when the virtual object exactly falls on
the focal length of the eye piece. This adjustment of the telescope is
called Normal adjustment.
In this case length of the telescope will be f0+fe.

57. When Final image is formed at the least distance of distinct vision:
In this case lens formula can be applied for the eyepiece as
f
1
f
f
-
m
get
we
u
f
-
m
ion
magnificat
for
equation
in the
value
this
ng
Substituti
f
1
f
1
D
1
f
1
u
1
f
1
u
-
1
-
D
-
1
get
eqution we
above
in
values
these
pluging
so
f
f
,
u
-
u
-D,
v
here
1
1
1
e
e
0
e
0
e
e
e
e
e
e
e
e


































D
D
f
u
v
From the above two cases it is clear that the fo should be greater than
fe . Negative sign in the formula indicates that the final image is
inverted. Magnification is max. when object is formed at D.

58. Reflecting Type Telescope
Reflecting telescopes can be used both for terrestrial and astronomical observations.
Consider a telescope whose objective has a focal length of 100 cm and the eyepiece
a focal length of 1 cm. The magnifying power of this telescope is
m = (fo/ue ) = 100/1 = 100 times(image is inverted)

59. For a brighter image the
objective lens should have
enough aperture to gather
all the light and its difficult
to manufacture