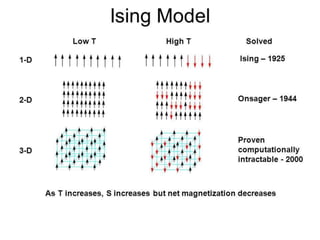
1. The Ising model is a statistical mechanics model of ferromagnetism. It represents magnetic dipole moments as "spins" on a lattice that can point in one of two directions and interact with neighboring spins. 2. The Ising model can explain phase transitions like ferromagnetism, anti-ferromagnetism, gas-liquid transitions, and liquid-solid transitions. 3. The statistical mechanics of the Ising model are studied using the Hamiltonian, which includes terms for spin-spin interaction energy and the energy of an external magnetic field interacting with the magnetic moments. Partition functions are then used to calculate thermodynamic properties.

1. Ising Model
Presentation on “Advanced Statistical Mechanics (PHY604)”
to
Dr. Khalid Mahmood Khattak
By
Muhammad Usama Daud (12987)
Riphah International University Faisalabad

2. Introduction
• This model was given by Ising (student of Lenz)
during his PHD.
• It is a dynamical model of phase transition.
• There is a model:
“Array of lattice sites, with only nearest
neighbor (n.n) interaction that depends upon
the manner of occupation of neighboring
sites.”

5. What can be explained by this model?
• This model can explain
1. Ferromagnetism and anti ferromagnetism
transition.
2. Gas to liquid transition.
3. Liquid to solid transition.

6. Study of Statistical mechanics of ising model
• To study the statistical mechanics:
1. We disregard K.E of atoms sitting at various lattice sites.
2. Phase transition is essentially result of interaction energy
among atoms and we include only nearest neighbors
interaction.
3. To study properties such as magnetic susceptibility (χ) we
subject the lattice to external magnetic field B. (Directed
upward)
4. The spin σi, then possess additional potential energy
Here μ=atomic magnetic moment=
g= lande g Factor
μB= Bohr Magneton
−𝐵𝜇𝜎𝑖
𝒈𝝁 𝒃 𝒋(𝒋 + 𝟏)

8. Bohr Magneton

9. Statistical Mechanics of Ising model
• Consider a system in the configuration {σ1, σ2, σ3,……,
σn }
• After applying external magnetic field
So the Hamiltonian of above configuration

10. •The 1st term is due to interaction of spin with magnetic field.
•In the 2nd term both of sigma represents nearest neighbors .
•The 2nd term is due to exchange interaction term.
•To explain the concept of n.n in 2nd term , consider the given
triangle. All vertices have spin interaction with each other.
•If the spins are given by
•Then
𝜎1,𝜎2, 𝜎3

11.  if spins are in same direction,
𝜎𝑖 𝜎𝑗 =(1)(1)=1
 If spins are in opposite direction, then
𝜎𝑖 𝜎𝑗 =(1)(-1)=-1
The above equation is known as Ising model equation.
•Due to change in magnetic field:
•J is exchange energy/Ising Interaction/ Ising Energy
Exchange interaction occurs between identical particles.
This effect is due to wave function of indistinguishable particles
being subject to exchange symmetry.
It is Quantum mechanical effect.
For the given configuration of N particles
−𝜇𝐵𝜎1+ −𝜇𝐵𝜎2 + −𝜇𝐵𝜎3 … … … . . +(−𝜇𝐵𝜎 𝑛 )
= −𝜇𝐵[𝜎1+ 𝜎2 + 𝜎3 … … … . . +(𝜎 𝑛 )]=−𝜇𝐵 𝜎𝑖
𝑛
𝑖=1

12. Different Notations
• Some authors write in different ways:
𝐻 = −𝐽 𝑆𝑖 𝑆𝑗<𝑖,𝑗 > -𝜇𝐵 𝑆𝑖𝑖=𝑁 𝑆𝑖 = ±1
<𝑖,𝑗 > is sum over nearest neighbor.
Note:
𝑺𝒊 𝑺 𝒋𝒏.𝒏 = 𝑺𝒊 𝑺 𝒋 = 𝑺𝒊 𝑺𝒊+𝟏𝒊<𝒊,𝒋>

14. The Partition Function
𝑇ℎ𝑒 𝑝𝑎𝑟𝑡𝑖𝑡𝑖𝑜𝑛 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑐𝑎𝑛 𝑏𝑒 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑 𝑤𝑖𝑡ℎ 𝑡ℎ𝑒 ℎ𝑒𝑙𝑝 𝑜𝑓
𝑍 = 𝑔𝑛 𝑒−𝛽𝐸𝑖
𝑖
But in case of Ising model
𝑍 𝑁 𝐵, 𝑇 = 𝜎1
+ 𝜎2
+ 𝜎3
+ ⋯……….. 𝜎 𝑛
𝑒−𝛽𝐻 𝜎𝑖

15. When the partition function is found a lots of
properties can be calculated.
• Helmholtz Free Energy:
• Internal Energy:
• Specific Heat:
• Net Magnetization:
𝑀 𝐵, 𝑇 = −
𝜕𝑓
𝜕𝛽 𝑇

16. Net Magnetization
• If T<Tc (Critical Temperature) and B=0 i.e in the
absence of external field then net magnetization
gives spontaneous magnetization of the system.
• If it is non zero i.e B>0 and system would be:
1. Ferromagnetic T<Tc
2. Paramagnetic T>Tc

17. • The last property can be found by partition function is
Magnetic Susceptibility
• “It is measure of the extent to which material can be
magnetized in relation to applied field.
𝜒 𝑚 𝐵, 𝑇 = (
𝜕𝑀
𝜕𝐵
) 𝑇