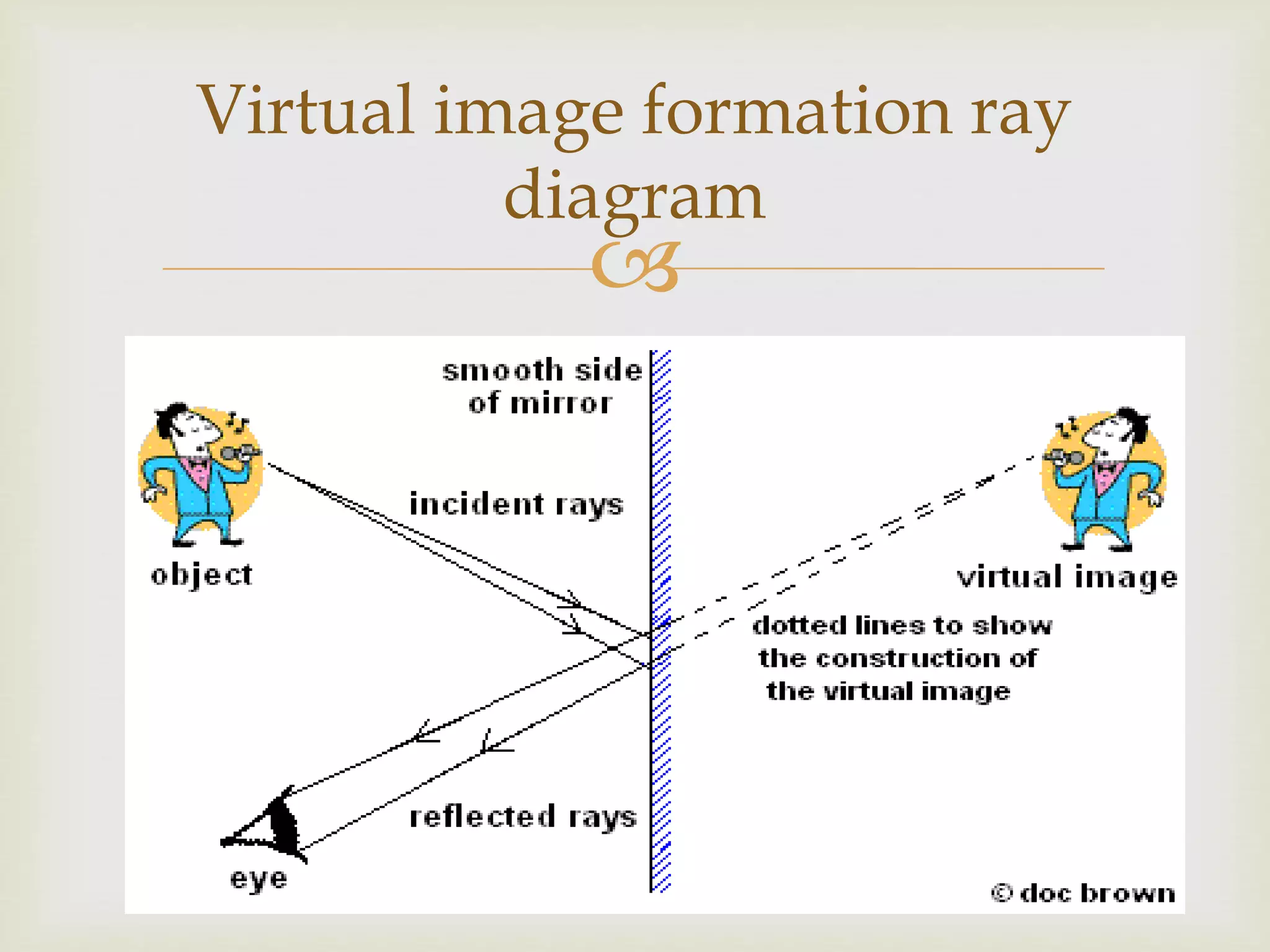
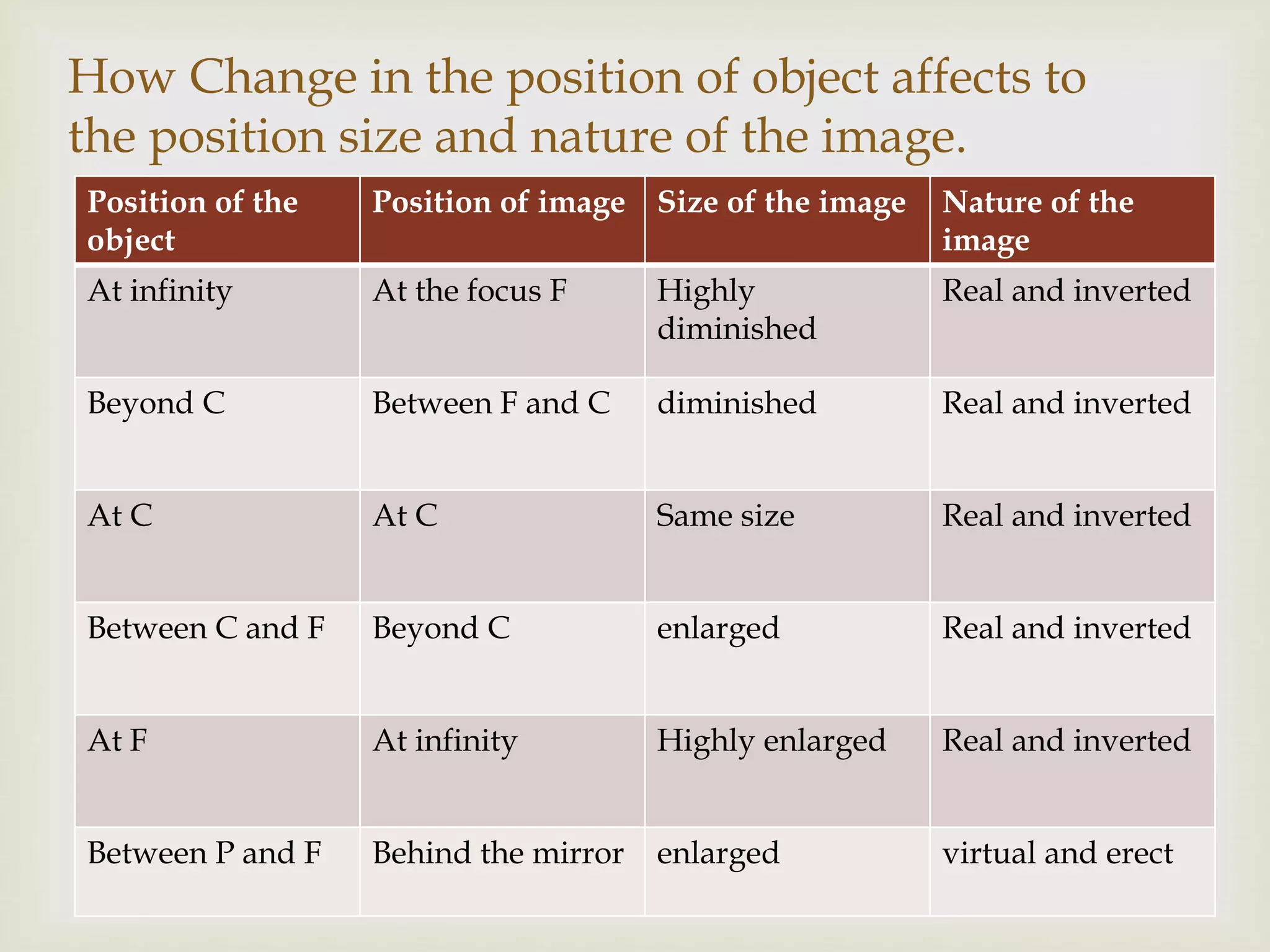
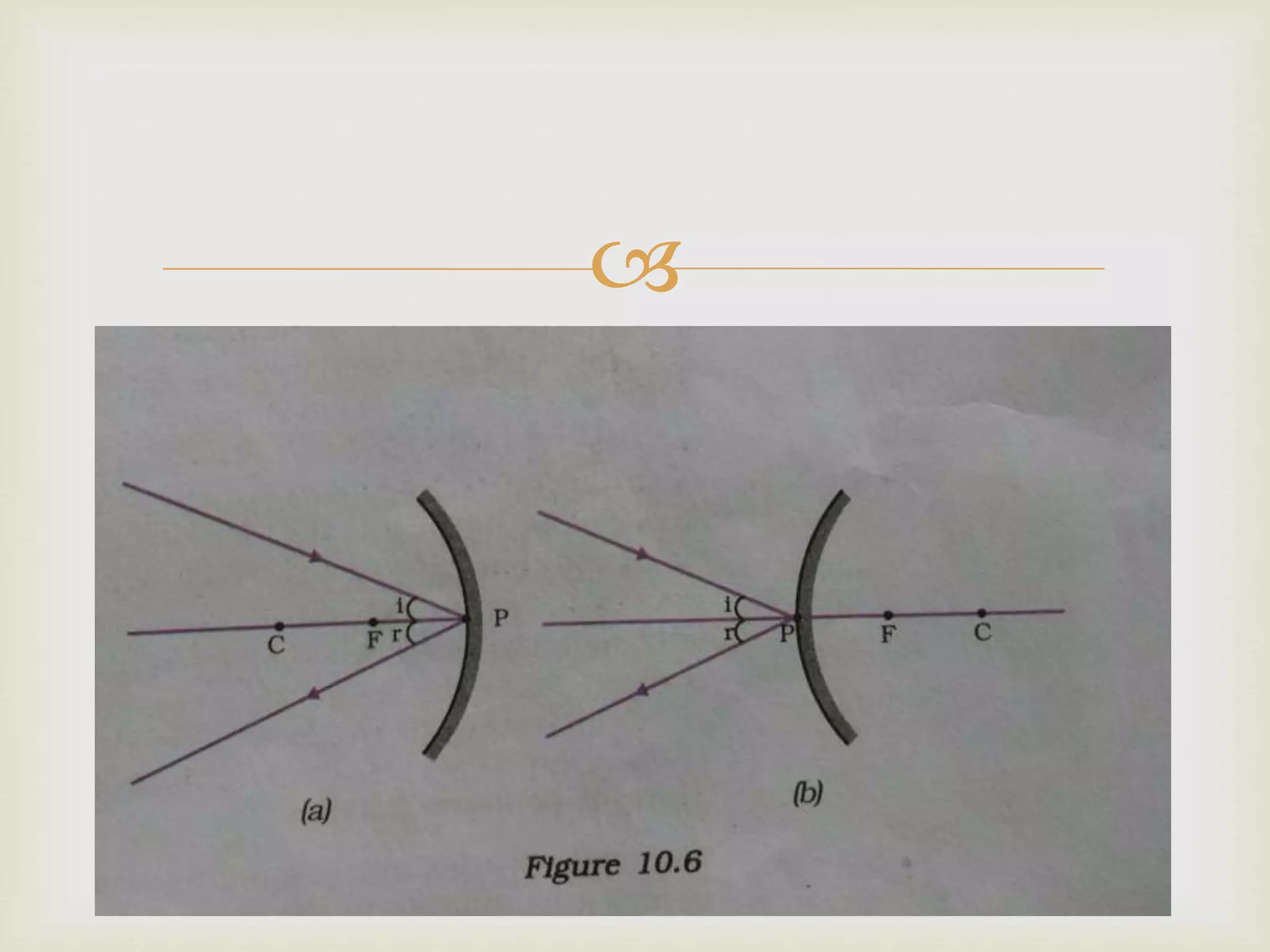
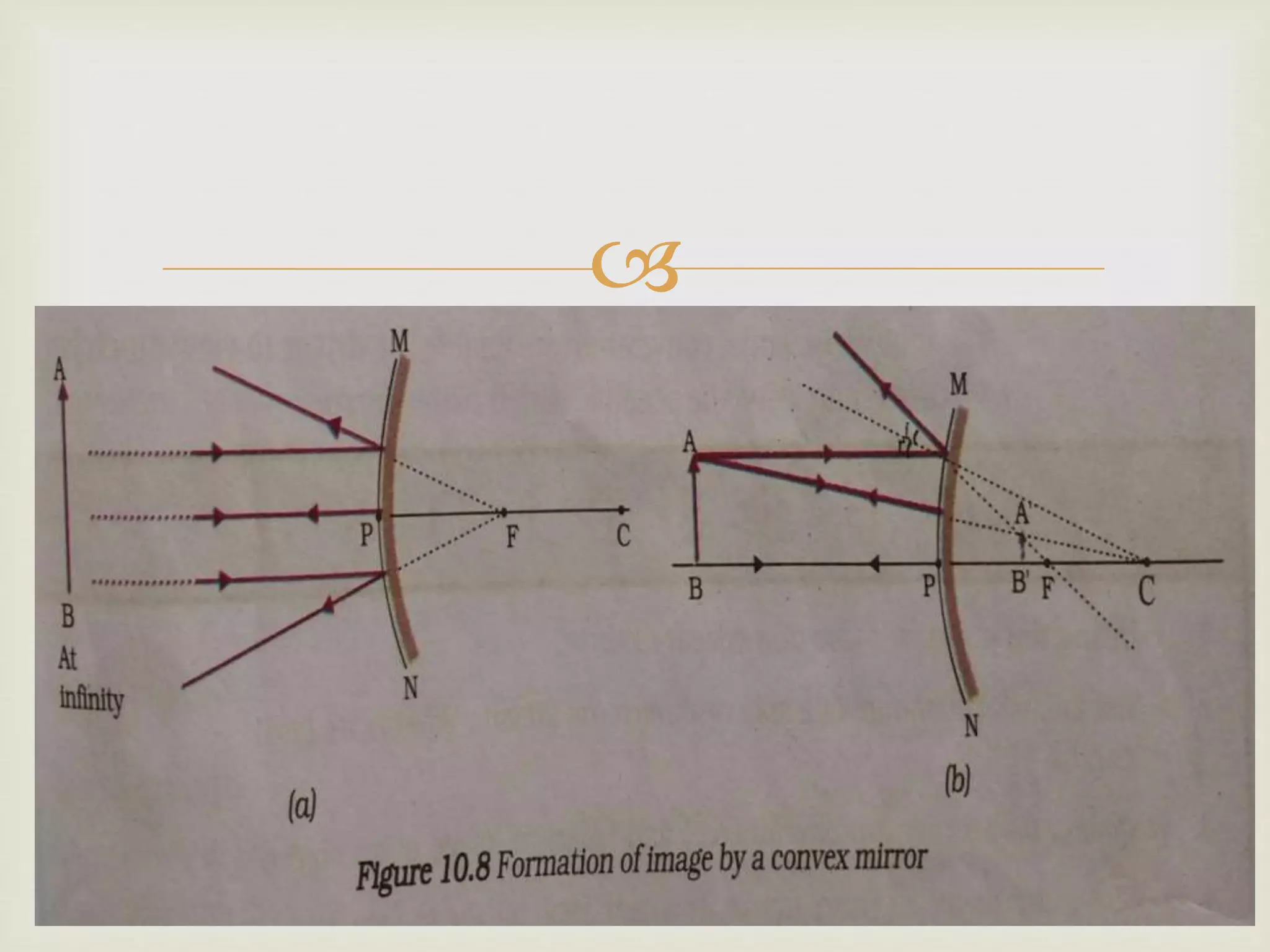
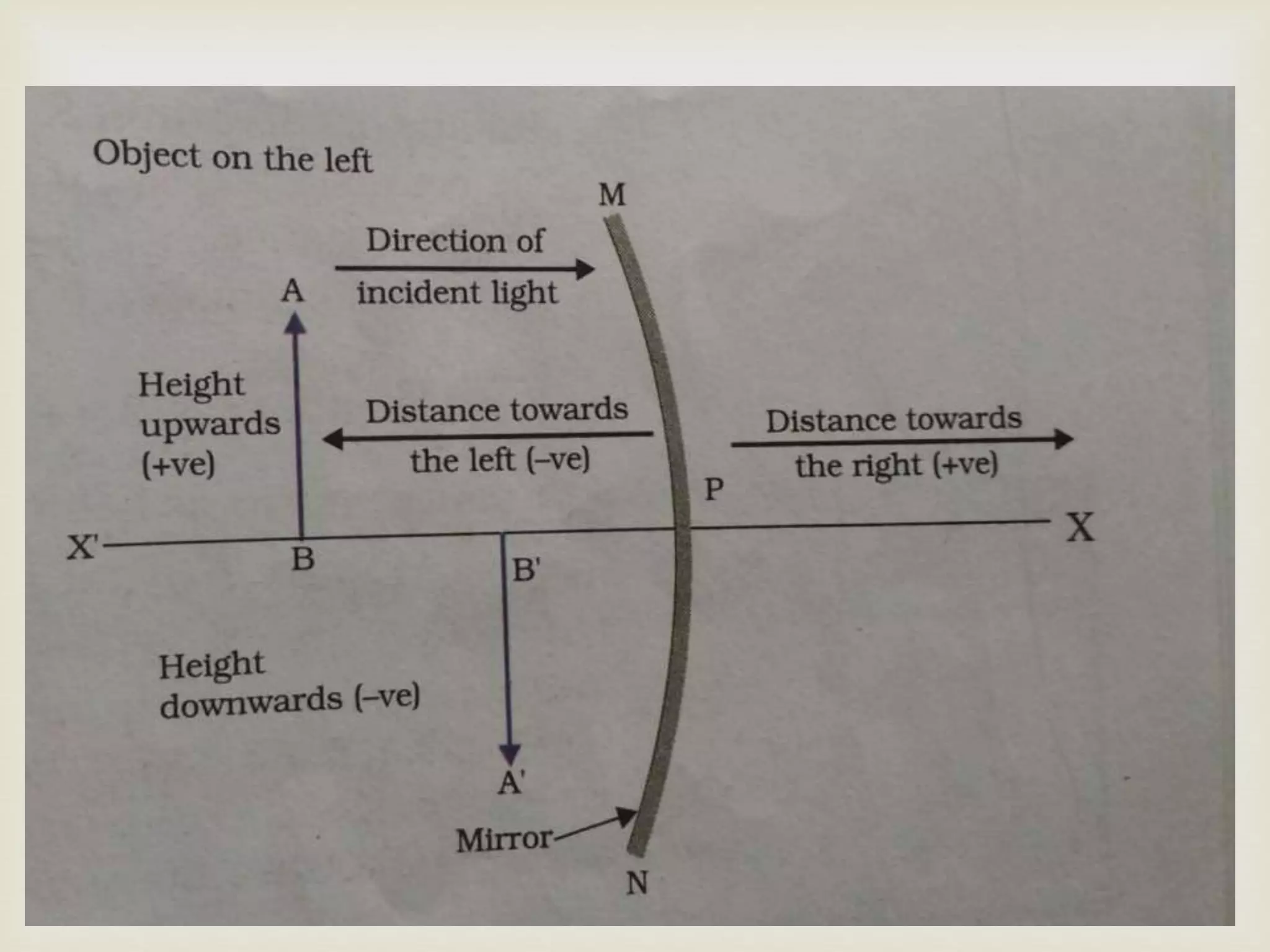
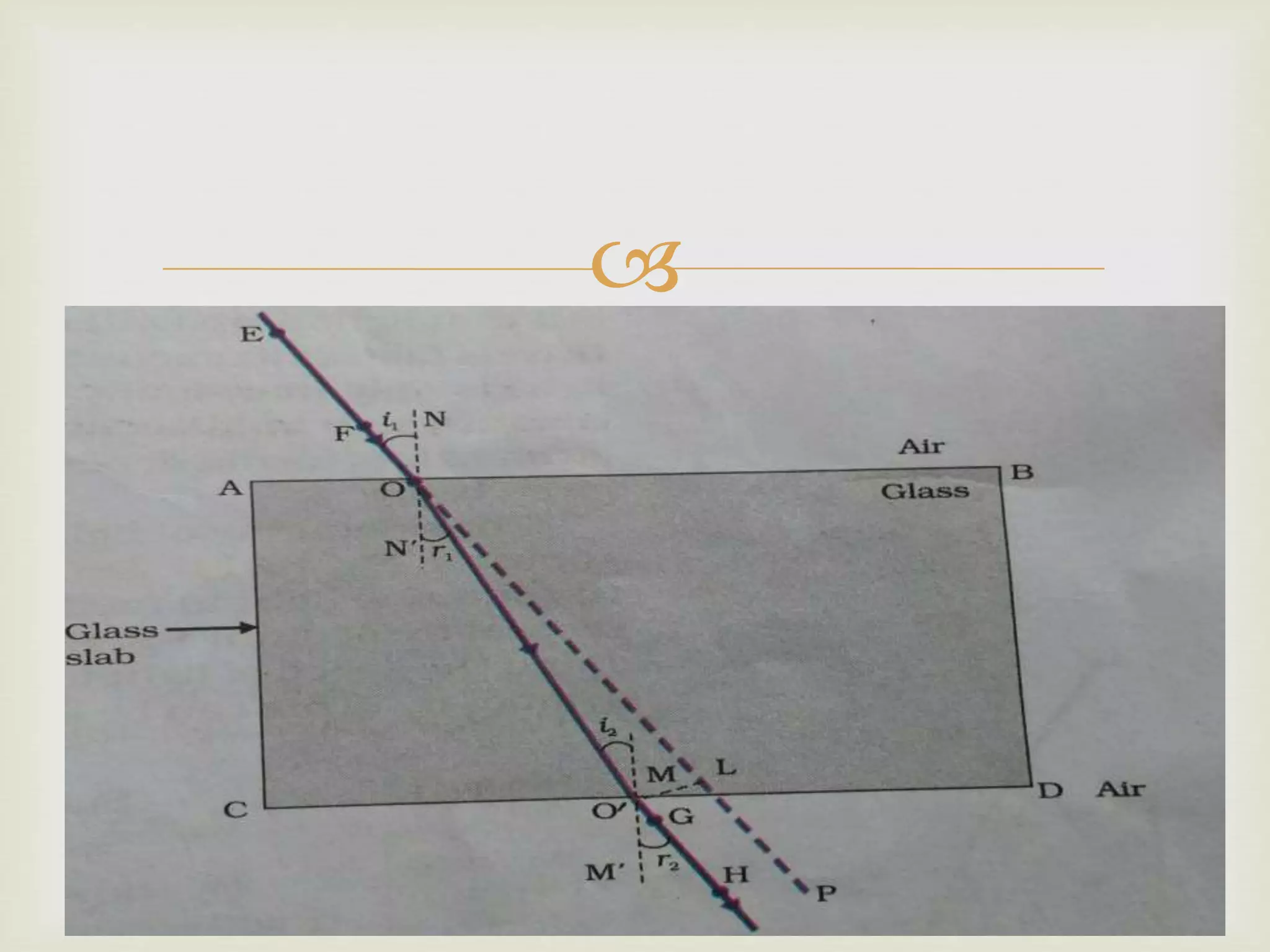
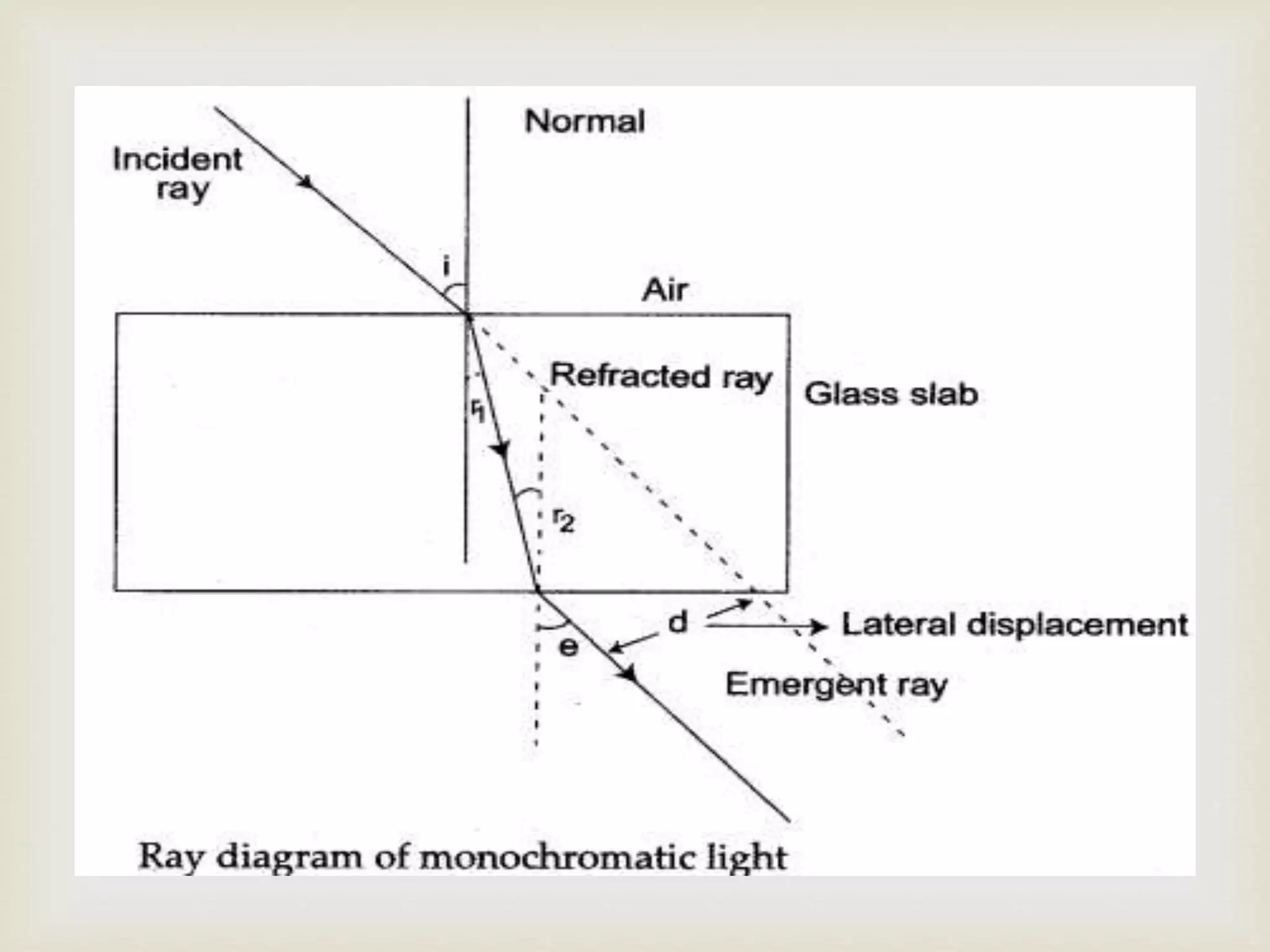
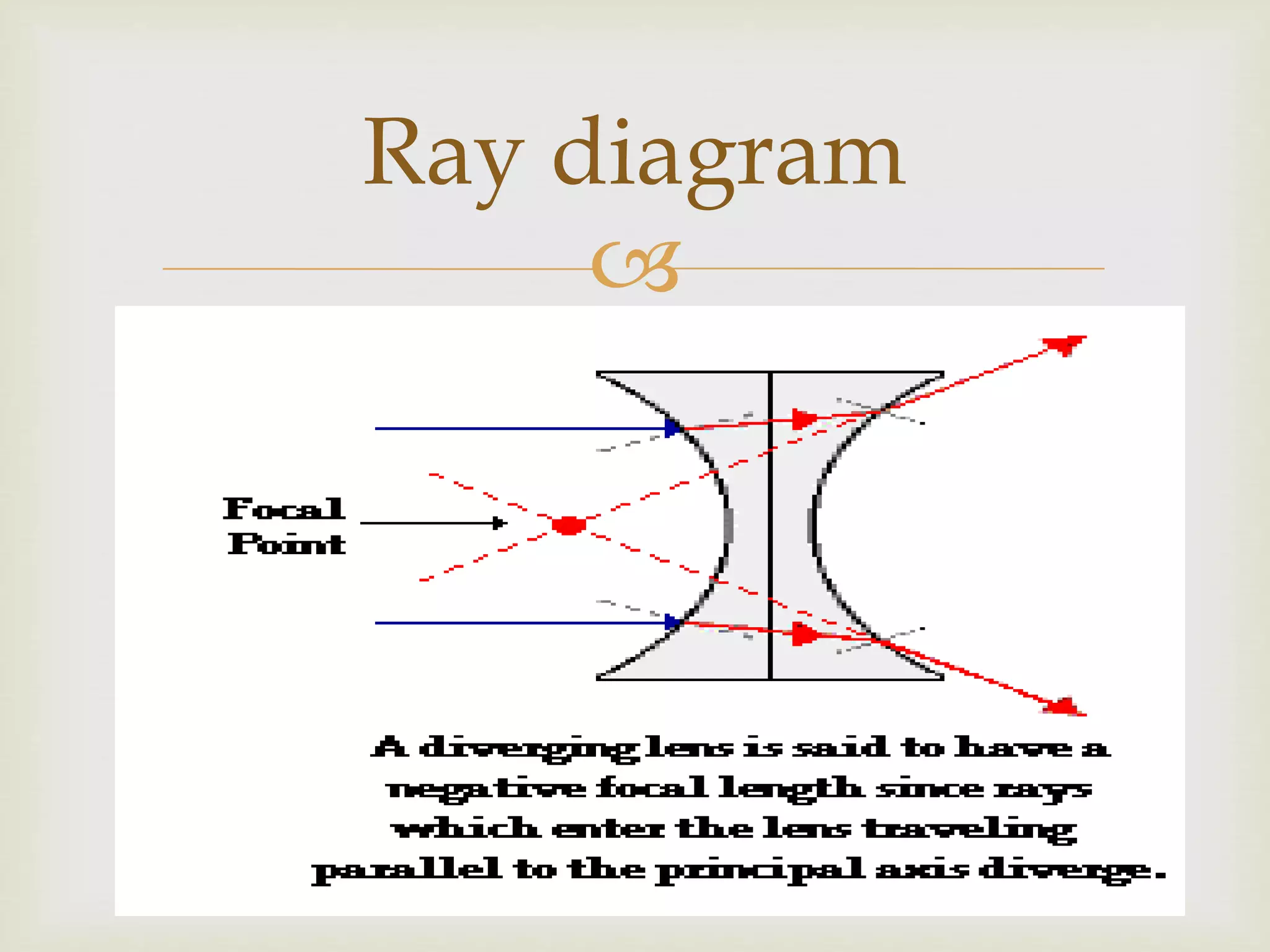
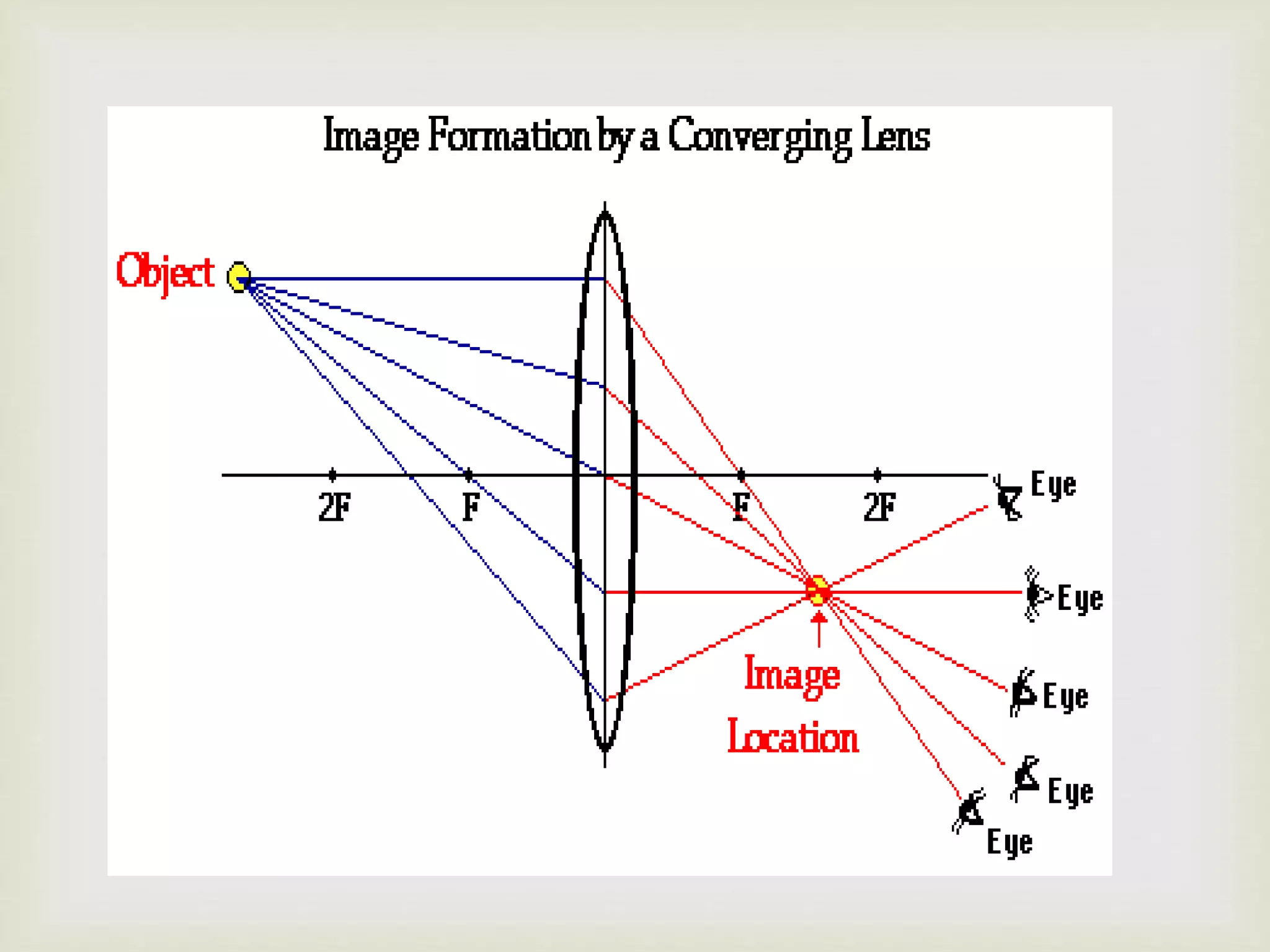
The document explains the principles of light reflection and refraction, including the laws of reflection, types of mirrors, and image formation in concave and convex mirrors. It details the characteristics of images, magnification, and the sign conventions used in spherical mirrors. Additionally, it covers the concept of lenses, their types, and how they refract light.