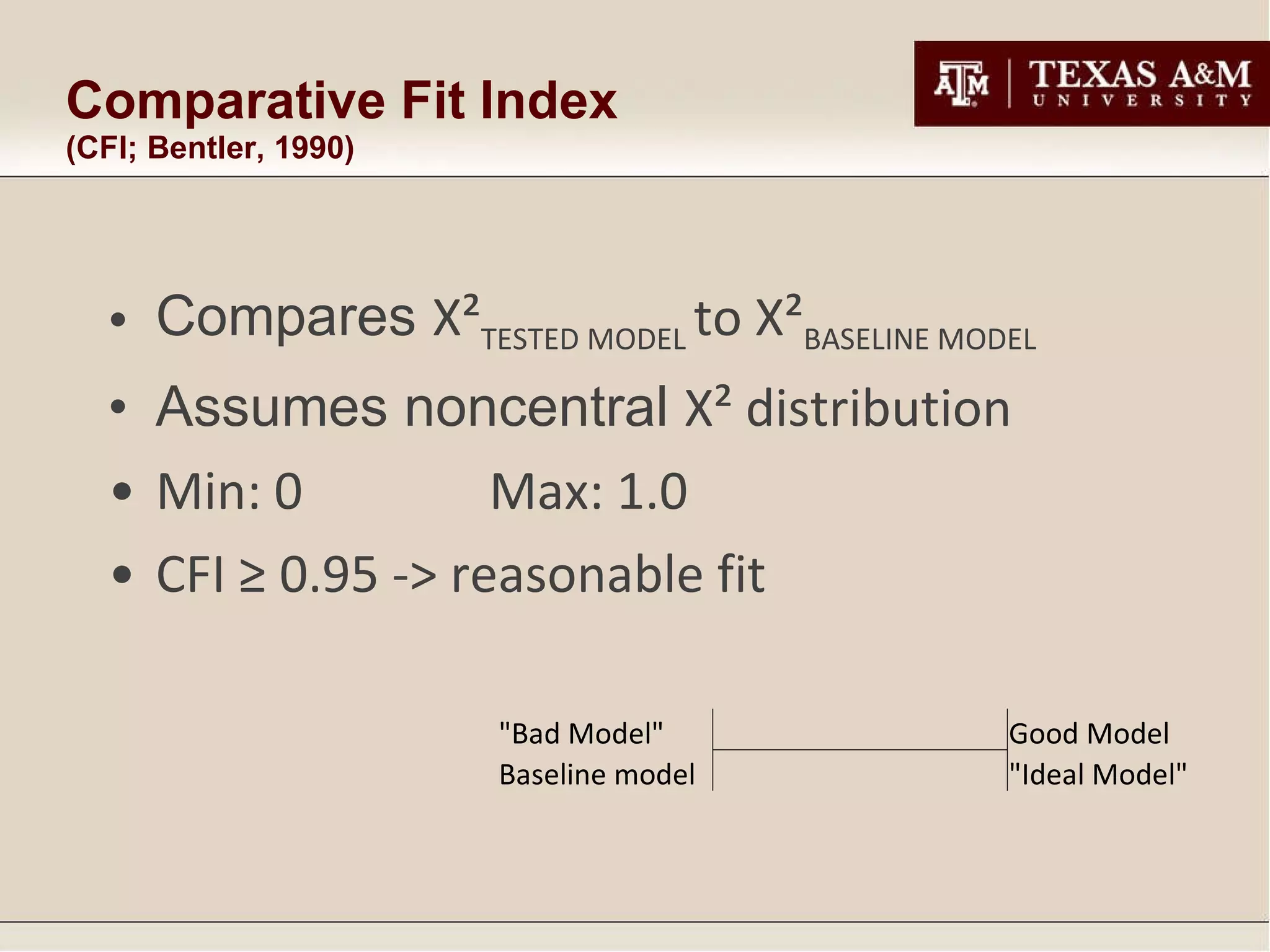
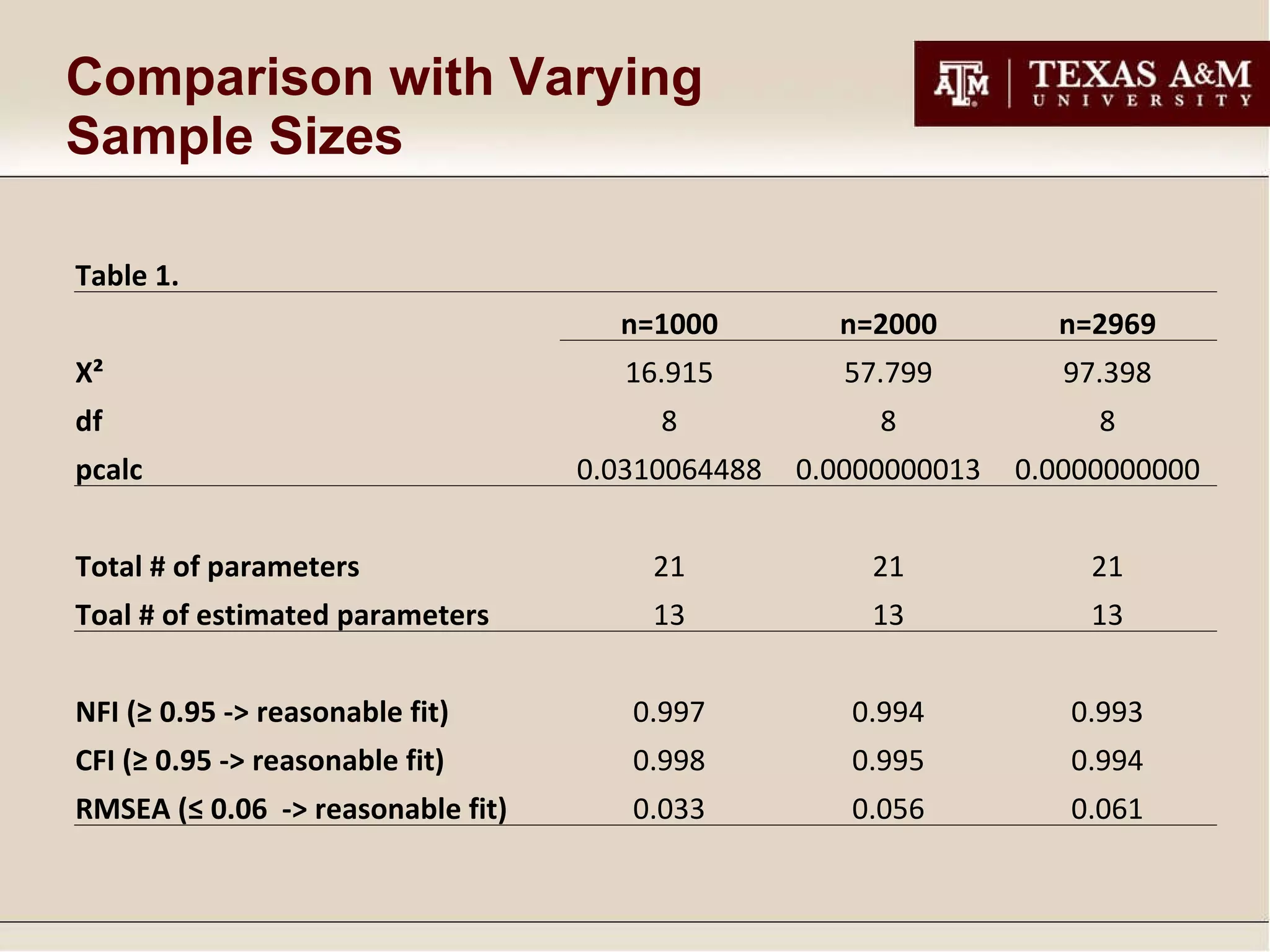
1. Researchers should consult multiple fit statistics when evaluating the fit of a confirmatory factor analysis model as no single statistic is ideal. 2. Different fit statistics were developed with different rationales and assess model fit in various ways. 3. Sample size impacts the chi-square statistic, with larger samples increasing the likelihood of rejection.

1. Confirmatory Factor Analysis Fit Statistics Nicola Ritter, M.Ed. EPSY 643: Multivariate Methods This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License .

2. Take Away Points Researchers should consult several fit statistics when evaluating model fit. There are similarities and differences between all fit statistics. Sample size impacts the chi-square statistic. There are numerous fit statistics. Fit statistics are estimated using a covariance matrix.

3. 5. Fit statistics are estimated using a covariance matrix. Analyze matrix of associations (i.e. covariance matrix) Recall: Pattern coefficients are the weights P VxF  P FxV ’ = R VxV + R VxX - R VxV + = R VxV -  Rodrigo Jimenez

4. Factor pattern coefficients to Fit Evaluation If P VxF perfectly reproduces R VxV + then, 1) R VxV - = 0 11... 0 1c 0 r1… 0 rc AND R VxV + = R VxX No information or variance left in the residual matrix

5. 4. There are numerous fit statistics. Most Common Fit Statistics Χ² statistical significance test Normed fit index (NFI; Bentler & Bonnett, 1980) Comparative fit index (CFI; Bentler, 1990) Root mean-square error of approximation (RMSEA; Steiger & Lind, 1980)

6. Chi-squared statistical significance test Compares sample matrix and reproduced matrix H 0 : R VxV = R VxV + H 0 : COV VxV = COV VxV + Here we do not want to reject the null hypothesis (i.e., not statistically significant) for models that we like.

7. Degrees of Freedom in Χ² test Function of the number of measured variables (n) and number of estimated parameters df TOTAL = n (n+1) / 2 Suppose: 6 variables df TOTAL = 6 (6+1) / 2 = 21 If 6 factor pattern coefficients, 6 error variances, and 1 factor covariance are estimated then: df MODEL = df TOTAL - # of estimated parameters df MODEL = 21 - 13 = 8

8. 3. Sample size impacts the chi-square statistic. Limitation of Χ² test Biased when: MLE is used Multivariate normality assumption is not met NOTE: Satorra & Bentler (1994) propose a correction Influenced by sample size, not useful in evaluating the fit of a single model Demonstrate in AMOS Location of Fit Statistics in Output Change in Χ² and p calc No change in parameters and fit statistics

9. Comparison with Varying Sample Sizes Table 1. n=1000 n=2000 n=2969 Χ² 16.915 57.799 97.398 df 8 8 8 pcalc 0.0310064488 0.0000000013 0.0000000000 Total # of parameters 21 21 21 Toal # of estimated parameters 13 13 13 NFI (≥ 0.95 -> reasonable fit) 0.997 0.994 0.993 CFI (≥ 0.95 -> reasonable fit) 0.998 0.995 0.994 RMSEA (≤ 0.06 -> reasonable fit) 0.033 0.056 0.061

10. Strength of Χ² test Helpful when comparing nested models Model A Model B

11. Normed Fit Index (NFI; Bentler & Bonnett, 1980) Compares Χ² TESTED MODEL to Χ² BASELINE MODEL Assumes measured variables are uncorrelated. Min: 0 Max: 1.0 NFI ≥ 0.95 -> reasonable fit "Bad Model" Good Model Baseline model "Ideal Model"

12. Comparative Fit Index (CFI; Bentler, 1990) Compares Χ² TESTED MODEL to Χ² BASELINE MODEL Assumes noncentral Χ² distribution Min: 0 Max: 1.0 CFI ≥ 0.95 -> reasonable fit "Bad Model" Good Model Baseline model "Ideal Model"

13. Root-mean-square error of approximation (RMSEA; Steiger & Lind, 1980) Compares sample COV matrix and population COV matrix Assumes measured variables are uncorrelated. (Bentler & Bonett, 1980) When: Sample COV matrix = population COV matrix RMSEA = 0 RMSEA ≤ 0.06 -> reasonable fit

14. Strength of RMSEA Relatively minimal influence by sample size Not overly influenced by estimation methods Sensitive to model misspecification (Fan, Thompson, & Wang, 1999)

15. 2. There are similarities and differences between all fit statistics. Table 2 NFI CFI RMSEA NFI Compares Χ² TESTED MODEL to Χ² BASELINE MODEL Assumes measured variables are uncorrelated. CFI Assumes noncentral Χ² distribution RMSEA Compares sample COV matrix and population COV matrix

16. 1. Researchers should consult several fit statistics when evaluating model fit. Fit indices were developed with different rationales. No single index will meet all our expectations for an ideal index (Fan, Thompson, & Wang, 1999)

17. Take Away Points Researchers should consult several fit statistics when evaluating model fit. There are similarities and differences between all fit statistics. Sample size impacts the chi-square statistic. There are numerous fit statistics. Fit statistics are estimated using a covariance matrix.

18. References Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107 , 238-246. Bentler, P. M., & Bonett, D. G. (1980). Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin, 88, 588-606. Fan. X., Thompson, B.. & Wang. L. (1999). Effects of sample size, estimation methods, and model specification on structural equation modeling fit indices. Structural Equation Modeling. 6, 56-83. Satorra, A. & Bentler, P. M. (1994). Corrections to test statistics and standard errors in covariance structural analysis. In A. von Eye & C. C. Clogg (Eds.), Latent variable analysis: Applications for developmental research (pp. 399-419). Thousand Oaks, CA: Sage. Steiger, J. H. & Lind, J. C. (1980, June). Statistically based test for the number of common factors. Paper presented at the annual meeting of the Psychometric Society, Iowa City, IA. Sun, J. (2005). Assessing goodness of fit in confirmatory factor analysis. Measurement and Evaluation in Counseling and Development, 37, 240- 256. Thompson, B. (2004). Exploratory and confirmatory factor analysis: Understanding concepts and applications . Washington, DC: American Psychological Association. (International Standard Book Number: 1-59147-093-5)