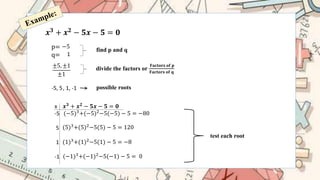
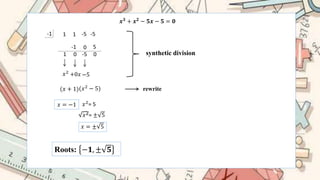
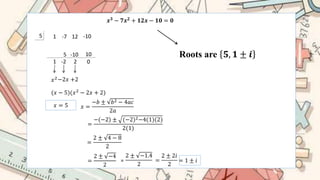
This document provides information about solving polynomials with irrational and imaginary roots. It begins with an introduction to irrational roots, noting that the polynomial coefficients must be rational. It then defines imaginary roots as occurring when the discriminant of a quadratic equation is negative. The document goes on to show examples of solving polynomials with rational number factorization and the quadratic formula to find irrational or imaginary roots. Roots found include irrational numbers like ±5 and imaginary numbers like 1±i. In all, the document demonstrates the process of finding all types of roots of polynomials.

1. Good Afternoon!
Hi, I am CARLO B. ANDRINO
M
a
t
h
e
m
a
t
i
c
s
1
0

2. 𝒙𝟑 + 𝟐𝒙𝟐 − 𝒙 + 𝟏𝟐 = 𝟎
𝟐𝒙𝟑 + 𝟐𝒙𝟐 − 𝒙 + 𝟏𝟓 = 𝟎
p=
q=
12
1
p=
q=
15
2
𝒘𝟒
+ 𝟐𝒘𝟑
− 𝟒𝒘𝟐
− 𝟐 = 𝟎
p=
q=
-2
1

3. RATIONAL ROOTS THEOREM
(irrational and imaginary roots)

4. Learning outcomes:
• Define the irrational and imaginary roots.
• Familiarize the steps on how to solve the
irrational and imaginary roots using the
polynomial theorems.
• Perform the solution in finding the irrational
and imaginary roots.

5. What is irrational
roots?
The irrational root theorem works only if the
coefficients of the polynomial are rational.

6. Imaginary roots
Reminder:
The imaginary unit is i.
𝑖2 = -1 or 𝑖 = −1
Imaginary roots appear in a quadratic equation when the
discriminant of the quadratic equation — the part under the
square root sign (𝑏2 – 4ac) — is negative.

7. 𝒙𝟑 + 𝒙𝟐 − 𝟓𝒙 − 𝟓 = 𝟎
p=
q=
−5
1
find p and q
±5, ±1
±1
divide the factors or
𝐅𝐚𝐜𝐭𝐨𝐫𝐬 𝐨𝐟 𝐩
𝐅𝐚𝐜𝐭𝐨𝐫𝐬 𝐨𝐟 𝐪
-5, 5, 1, -1 possible roots
x 𝒙𝟑 + 𝒙𝟐 − 𝟓𝒙 − 𝟓 = 𝟎
-5
5
1
-1
test each root
(−5)3
+(−5)2
−5(−5) − 5 = −80
(5)3
+(5)2
−5(5) − 5 = 120
(1)3
+(1)2
−5(1) − 5 = −8
(−1)3
+(−1)2
−5(−1) − 5 = 0

8. -1
𝒙𝟑
+ 𝒙𝟐
− 𝟓𝒙 − 𝟓 = 𝟎
1 1 -5 -5
1
-1
0
0
-5
5
0 synthetic division
𝑥2
+0𝑥 −5
(𝑥 + 1)(𝑥2 − 5) rewrite
𝑥 = −1 𝑥2
= 5
𝑥2= ± 5
𝑥 = ± 5
Roots: −𝟏, ± 𝟓

9. 𝒙𝟑 − 𝟕𝒙𝟐 + 𝟏𝟐𝒙 − 𝟏𝟎 = 𝟎
p=
q=
-10
1
±1, ±2, ±5, ±10
±1
-10, 10, -5, 5,-2, 2,-1, 1
x 𝒙𝟑 − 𝟕𝒙𝟐 + 𝟏𝟐𝒙 − 𝟏𝟎 = 𝟎
-10
10
-5
5
-2
2
-1
1
(−10)3
−7(−10)2
+12(−10) − 10 = −1830
(10)3
−7(10)2
+12(10) − 10 = 410
(−5)3−7(−5)2+12(−5) − 10 = −20
(5)3
−7(5)2
+12(5) − 10 = 0
(−2)3−7(−2)2+12(−2) − 10 = −70
(2)3
−7(2)2
+12(2) − 10 = −6
(−1)3−7(−1)2+12(−1) − 10 = −30
(1)3−7(1)2+12(1) − 10 = −4

10. 5
𝒙𝟑 − 𝟕𝒙𝟐 + 𝟏𝟐𝒙 − 𝟏𝟎 = 𝟎
1 -7 12 -10
1
5
-2
-10
2
10
0
(𝑥 − 5)(𝑥2
− 2𝑥 + 2)
𝑥2−2𝑥 +2
𝑥 = 5 𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
=
−(−2) ± (−2)2−4(1)(2)
2(1)
=
2 ± 4 − 8
2
=
2 ± −4
2
=
2 ± −1.4
2
=
2 ± 2𝑖
2
= 1 ± 𝑖
Roots are 𝟓, 𝟏 ± 𝒊

11. 𝒙𝟑 + 𝟐𝒙𝟐 − 𝟑𝒙 − 𝟔 = 𝟎
p=
q=
-6
1
_________________
±1, ±2, ±3, ±6
±1
-6, 6, -3, 3, -2, 2, -1, 1
x 𝒙𝟑 + 𝟐𝒙𝟐 − 𝟑𝒙 − 𝟔
-6
6
-3
3
-2
2
-1
1
(−6)3
+2(−6)2
−3(−6) − 6 =
(6)3
+2(6)2
−3(6) − 6 =
(−3)3
+2(−3)2
−3(−3) − 6 =
(3)3+2(3)2−3(3) − 6 =
(−2)3+2(−2)2−3(−2) − 6 =
(2)3+2(2)2−3(2) − 6 =
(−1)3
+2(−1)2
−3(−1) − 6 =
(1)3+2(1)2−3(1) − 6 =
132
264
-6
30
0
4
−8
−6

12. -2
𝒙𝟑 + 𝟐𝒙𝟐 − 𝟑𝒙 − 𝟔
1 2 -3 -6
1
-2
0
0
-3
6
0
𝑥2
+0𝑥-3
(𝑥 + 2)(𝑥2 − 3)
𝑥 = −2 𝑥2
= 3
𝑥2 = ± 3
𝑥 = ± 3
Roots are −𝟐, ± 𝟑

13. Thank you
for listening!