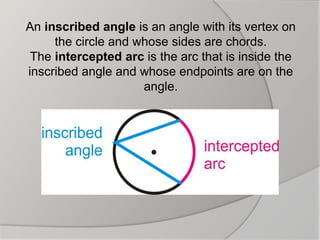
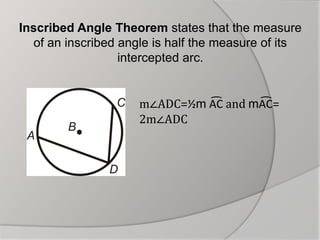
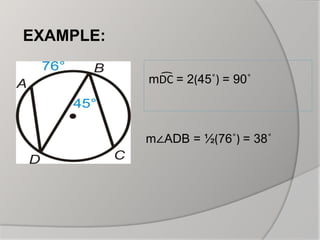
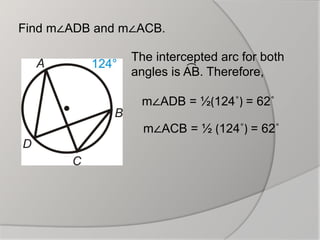
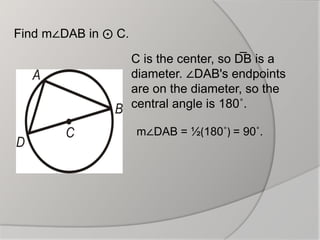
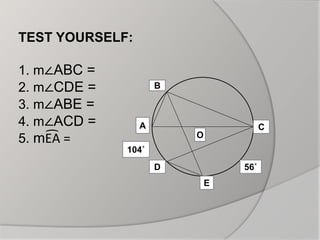
The document discusses inscribed angles in circles. It defines an inscribed angle as an angle whose vertex is on the circle and whose sides are chords. The intercepted arc is the arc inside the inscribed angle between its sides. The inscribed angle theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. Congruent inscribed angles intercept the same arc and are equal. A right angle intercepts a semicircle. Examples are given to demonstrate finding the measures of inscribed angles using these properties.

2. OBJECTIVES:
• Understand and apply the concept of an inscribed
angle of a circle.
• Familiarize the ways on how to solve the inscribed
angle and its arc.
• To solve the given measure of an inscribed angle
and its arc.

6. An inscribed angle is an angle with its vertex on
the circle and whose sides are chords.
The intercepted arc is the arc that is inside the
inscribed angle and whose endpoints are on the
angle.

7. Inscribed Angle Theorem states that the measure
of an inscribed angle is half the measure of its
intercepted arc.
m∠ADC=½m A͡C and mA͡C=
2m∠ADC

8. Congruent Inscribed Angles Theorem are
inscribed angle that intercept the same arc are
congruent.
∠ADB and ∠ACB intercept A͡B,
so m∠ADB = m∠ACB.
Similarly, ∠DAC and ∠DBC
Intercept D͡͡C,
so m∠DAC = m∠DBC.

9. An angle intercepts a semicircle if and only if it is a
right angle (Semicircle Theorem). Anytime a right
angle is inscribed in a circle, the endpoints of the
angle are the endpoints of a diameter and the
diameter is the hypotenuse.

10. mD͡C = 2(45˚) = 90˚
EXAMPLE:
m∠ADB = ½(76˚) = 38˚

11. Find m∠ADB and m∠ACB.
The intercepted arc for both
angles is A
͡ B. Therefore,
m∠ADB = ½(124˚) = 62˚
m∠ACB = ½ (124˚) = 62˚

12. Find m∠DAB in ⨀ C.
C is the center, so D
͞ B is a
diameter. ∠DAB's endpoints
are on the diameter, so the
central angle is 180˚.
m∠DAB = ½(180˚) = 90˚.

13. TEST YOURSELF:
1. m∠ABC =
2. m∠CDE =
3. m∠ABE =
4. m∠ACD =
5. mE͡A =
A
B
D
C
E
O
56˚
104˚